bootridge
Empirical Bayes penalized regression for univariate or multivariate outcomes,
with shrinkage tuned to minimize prediction error computed by .632 bootstrap.
-- Function File: bootridge (Y, X)
-- Function File: bootridge (Y, X, CATEGOR)
-- Function File: bootridge (Y, X, CATEGOR, NBOOT)
-- Function File: bootridge (Y, X, CATEGOR, NBOOT, ALPHA)
-- Function File: bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L)
-- Function File: bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L, DEFF)
-- Function File: bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L, DEFF, SEED)
-- Function File: bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L, DEFF, SEED, TOL)
-- Function File: S = bootridge (Y, X, ...)
-- Function File: [S, YHAT] = bootridge (Y, X, ...)
'bootridge (Y, X)' fits an empirical Bayes ridge regression model using
a linear Normal (Gaussian) likelihood with an empirical Bayes normal
ridge prior on the regression coefficients. The ridge tuning constant
(lambda) is optimized via .632 bootstrap-based machine learning (ML) to
minimize out-of-bag prediction error [1, 2]. Y is an m-by-q matrix of
outcomes and X is an m-by-n design matrix whose first column must
correspond to an intercept term. If an intercept term (a column of ones)
is not found in the first column of X, one is added automatically. If any
rows of X or Y contain missing values (NaN) or infinite values (+/- Inf),
the corresponding observations are omitted before fitting.
For each outcome, the function prints posterior summaries for regression
coefficients or linear estimates, including posterior means, equal-tailed
credible intervals, Bayes factors (lnBF10), and the marginal prior used
for inference. When multiple outcomes are fitted (q > 1), the function
additionally prints posterior summaries for the residual correlations
between outcomes, reported as unique (lower-triangular) outcome pairs.
For each correlation, the printed output includes the estimated
correlation and its credible interval.
Interpretation note (empirical Bayes):
Bayes factors reported by 'bootridge' are empirical‑Bayes approximations
based on a data‑tuned ridge prior. They are best viewed as model‑
comparison diagnostics (evidence on a predictive, information‑theoretic
scale) rather than literal posterior odds under a fully specified prior
[3–5]. The log scale (lnBF10) is numerically stable and recommended
for interpretation; BF10 may be shown as 0 or Inf when beyond machine
range, while lnBF10 remains finite. These Bayesian statistics converge
to standard conjugate Bayesian evidence as the effective residual
degrees of freedom (df_t) increase.
For convenience, the statistics-resampling package also provides the
function `bootlm`, which offers a user-friendly but feature-rich interface
for fitting univariate linear models with continuous and categorical
predictors. The design matrix X and hypothesis matrix L returned in the
MAT-file produced by `bootlm` can be supplied directly to `bootridge`.
The outputs of `bootlm` also provide a consistent definition of the model
coefficients, thereby facilitating interpretation of parameter estimates,
contrasts, and posterior summaries. The design matrix X and hypothesis
matrix L can also be obtained the same way with one of the outcomes of a
multivariate data set, then fit to all the outcomes using bootridge.
'bootridge (Y, X, CATEGOR)' specifies the predictor columns that
correspond to categorical variables. CATEGOR must be a scalar or vector
of integer column indices referring to columns of X (excluding the
intercept). Alternatively, if all predictor terms are categorical, set
CATEGOR to 'all' or '*'. CATEGOR does NOT create or modify dummy or
contrast coding; users are responsible for supplying an appropriately
coded design matrix X. The indices in CATEGOR are used to identify
predictors that represent categorical variables, even when X is already
coded, so that variance-based penalty scaling is not applied to these
terms.
For categorical predictors in ridge regression, use meaningful centered
and preferably orthogonal (e.g. Helmert or polynomial) contrasts whenever
possible, since shrinkage occurs column-wise in the coefficient basis.
Orthogonality leads to more stable shrinkage and tuning of the ridge
parameter. Although the prior is not rotationally invariant, Bayes
factors for linear contrasts defined via a hypothesis matrix (L) are
typically more stable when the contrasts defining the coefficients are
orthogonal.
'bootridge (Y, X, CATEGOR, NBOOT)' sets the number of bootstrap samples
used to estimate the .632 bootstrap prediction error. The bootstrap* has
first order balance to improve the efficiency for variance estimation,
and utilizes bootknife (leave-one-out) resampling to guarantee
observations in the out-of-bag samples. The default value of NBOOT is
100, but more resamples are recommended to reduce monte carlo error.
The bootstrap tuning of the ridge parameter relies on resampling
functionality provided by the statistics-resampling package. In
particular, `bootridge` depends on the functions `bootstrp` and `boot` to
perform balanced bootstrap and bootknife (leave-one-out) resampling and
generate out-of-bag samples. These functions are required for estimation
of the .632 bootstrap prediction error used to select the ridge tuning
constant.
'bootridge (Y, X, CATEGOR, NBOOT, ALPHA)' sets the central mass of equal-
tailed credibility intervals (CI) to (1 - ALPHA) with probability mass
ALPHA/2 in each tail, and sets the threshold for the adjusted stability
selection (SS) probabilities of the regression coefficients to (1 - ALPHA).
ALPHA must be a scalar value between 0 and 1. The default value of ALPHA
is 0.05 for 95% intervals.
'bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L)' specifies a hypothesis
matrix L of size n-by-c defining c linear contrasts or model-based
estimates of the regression coefficients. In this case, posterior
summaries and credible intervals are reported for the linear estimates
rather than the model coefficients.
'bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L, DEFF)' specifies a design
effect used to account for clustering or dependence. DEFF inflates the
posterior covariance and reduces the effective degrees of freedom (df_t)
to ensure Bayes factors and intervals are calibrated for the effective
sample size. For a mean, Kish's formula DEFF = 1+(g-1)*r (where g is
cluster size) suggests an upper bound of g. However, for regression
slopes, the realized DEFF depends on the predictor type: it can exceed
g for between-cluster predictors or be less than 1 for within-cluster
predictors. DEFF is best estimated as the ratio of clustered-to-i.i.d.
sampling variances - please see DETAIL below. Default DEFF is 1.
'bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L, DEFF, SEED)' initialises the
Mersenne Twister random number generator using an integer SEED value so
that bootstrap results are reproducible, which improves convergence.
Monte carlo error of the results can be assessed by repeating the
analysis multiple times, each time with a different random seed.
'bootridge (Y, X, CATEGOR, NBOOT, ALPHA, L, DEFF, SEED, TOL)' controls
the convergence tolerance for optimizing the ridge tuning constant lambda
on the log10 scale. Hyperparameter optimization terminates when the width
of the current bracket satisfies:
log10 (lambda_high) − log10 (lambda_low) < TOL.
Thus, TOL determines the relative (multiplicative) precision of lambda.
The default value TOL = 0.005 corresponds to approximately a 1% change in
lambda, which is typically well below the Monte Carlo noise of the .632
bootstrap estimate of prediction error.
* If sufficient parallel resources are available (three or more workers),
the optimization uses a parallel k‑section search; otherwise, a serial
golden‑section search is used. The tolerance TOL applies identically
in both cases. The benefit of parallel processing is most evident when
NBOOT is very large. In GNU Octave, the maximum number of workers used
can be set by the user before running bootridge, for example, for three
workers with the command:
setenv ('OMP_NUM_THREADS', '3')
'S = bootridge (Y, X, ...)' returns a structure containing posterior
summaries including posterior means, credibility intervals, Bayes factors,
prior summaries, the bootstrap-optimized ridge parameter, residual
covariance estimates, and additional diagnostic information.
The output S is a structure containing the following fields (listed in
order of appearance):
o coefficient
n-by-q matrix of posterior mean regression coefficients for each
outcome when no hypothesis matrix L is specified.
o estimate
c-by-q matrix of posterior mean linear estimates when a hypothesis
matrix L is specified. This field is returned instead of
'coefficient' when L is non-empty.
o CI_lower
Matrix of lower bounds of the (1 - ALPHA) credibility intervals
for coefficients or linear estimates. Dimensions match those of
'coefficient' or 'estimate'.
o CI_upper
Matrix of upper bounds of the (1 - ALPHA) credibility intervals
for coefficients or linear estimates. Dimensions match those of
'coefficient' or 'estimate'.
o BF10
Matrix of Bayes factors (BF10) for testing whether each regression
coefficient or linear estimate equals zero, computed using the
Savage–Dickey density ratio. Values may be reported as 0 or Inf
when outside floating‑point range; lnBF10 remains finite and is
the recommended evidential scale.
o lnBF10
Matrix of natural logarithms of the Bayes factors (BF10). Positive
values indicate evidence in favour of the alternative hypothesis,
whereas negative values indicate evidence in favour of the null.
lnBF10 < -1 is approx. BF10 < 0.3
lnBF10 > +1 is approx. BF10 > 3.0
o prior
Cell array describing the marginal inference-scale prior used for
each coefficient or estimate in Bayes factor computation.
Reported as 't (mu, sigma, df_t)' on the coefficient (or estimate)
scale; see CONDITIONAL VS MARGINAL PRIORS for details.
o Deff
Design effect used to inflate the residual covariance and reduce
inferential degrees of freedom to account for clustering.
o lambda
Scalar ridge tuning constant selected by minimizing the .632
bootstrap estimate of prediction error (then scaled by DEFF).
o df_lambda
Effective residual degrees of freedom under ridge regression,
defined as m minus the trace of the ridge hat matrix. Used for
residual variance estimation (scale); does NOT include DEFF.
o df_t
Inferential degrees of freedom, which is df_lambda adjusted for
for the design effect.
o Sigma_Y_hat
Estimated residual covariance matrix of the outcomes, inflated by
the design effect DEFF when applicable. For a univariate outcome,
this reduces to the residual variance.
o tau2_hat
Estimated prior covariance of the regression coefficients across
outcomes, proportional to Sigma_Y_hat and inversely proportional
to the ridge parameter lambda.
o Sigma_Beta
Cell array of posterior covariance matrices of the regression
coefficients. Each cell corresponds to one outcome and contains
the covariance matrix for that outcome.
o nboot
Number of bootstrap samples used to estimate the .632 bootstrap
prediction error.
o tol
Numeric tolerance used in the golden-section search for optimizing
the ridge tuning constant.
o iter
Number of iterations performed by the golden-section search.
o pred_err
The minimized prediction error calculated using the optimal lambda.
Note that pred_err calculation is based on the outcome variables
(columns) in Y after internal standardization, and the predictors
X after internal centering.
o stability
The probabilities that the sign of the regression coefficients
remained consistent across max(nboot,1999) bootstrap resamples [6].
Raw probabilities are smoothed using a Jeffreys prior and, if
applicable, adjusted by the design effect (Deff). In the printed
summary, stability exceeding (1 - ALPHA / 2) is indicated by (+)
or (-) to denote the consistent direction of the effect.
o RTAB
Matrix summarizing residual correlations (strictly lower-
triangular pairs). The columns correspond to outcome J, outcome I,
and the coefficient and credible intervals for their correlation.
Credible intervals for correlations are computed on Fisher’s z
[7] using a t‑based sampling distribution with effective degrees
of freedom df_t, and then back‑transformed. See CONDITIONAL VS
MARGINAL PRIORS and DETAIL below. Diagonal entries are undefined
and not included.
o P_vec
A vector of predictor-wise penalty weights used to normalize
shrinkage across the predictor terms.
'[S, YHAT] = bootridge (Y, X, ...)' returns fitted values.
DETAIL: The model implements an empirical Bayes ridge regression that
simultaneously addresses the problems of multicollinearity, multiple
comparisons, and clustered dependence. The sections below provide
detail on the applications to which this model is well suited and the
principles of its operation.
REGULARIZATION AND MULTIPLE COMPARISONS:
Unlike classical frequentist methods (e.g., Bonferroni) that penalize
inference-stage decisions (p-values), `bootridge` penalizes the estimates
themselves via shrinkage. By pooling information across all predictors to
learn the global penalty (lambda), the model automatically adjusts its
skepticism to the design's complexity. This provides a principled
probabilistic alternative to family-wise error correction: noise-driven
effects are shrunken toward zero, while stable effects survive the
penalty. This "Partial Pooling" ensures that Bayes factors are
appropriately conservative without the catastrophic loss of power
associated with classical post-hoc adjustments [8, 9]. See later section
on STATISTICAL INFERENCE AND ERROR CONTROL.
PREDICTIVE OPTIMIZATION:
The ridge tuning constant (hyperparameter) is selected empirically by
minimizing the .632 bootstrap estimate of prediction error [1, 2]. This
aligns lambda with minimum estimated out‑of‑sample mean squared
prediction error, ensuring the model is optimized for generalizability
rather than mere in-sample fit [10–12]. This lambda in turn determines the
scale of the Normal ridge prior used to shrink slope coefficients toward
zero [13].
CONDITIONAL VS MARGINAL PRIORS:
The ridge penalty (lambda) corresponds to a Normal prior on the
regression coefficients CONDITIONAL on the residual variance:
Beta | sigma^2 ~ Normal(0, tau^2 * sigma^2),
where tau^2 is determined by lambda. This conditional Normal prior
fully defines the ridge objective function and is held fixed during
lambda optimisation (prediction-error minimisation).
For inference, however, uncertainty in the residual variance is
explicitly acknowledged. Integrating over variance uncertainty under
an empirical‑Bayes approximation induces a marginal Student’s t
distribution for coefficients and linear estimates, which is used
for credible intervals and Bayes factors.
PRIOR CALIBRATION & DATA INDEPENDENCE:
To prevent circularity in the prior selection, lambda is optimized
solely by minimizing the .632 bootstrap out-of-bag (OOB) error.
This ensures the prior precision is determined by the model's
ability to predict "unseen" observations (data points not used
for the coefficient estimation in a given bootstrap draw),
thereby maintaining a principled separation between the data used
for likelihood estimation and the data used for prior tuning.
STABILITY SELECTION:
The directional reproducibility of the sign of the regression coefficients
under resampling are quantified and reported as Stability Selection (SS).
It is possible for a shrunken coefficient to be highly stable in sign
despite having anecdotal Bayes Factors.
BAYES FACTORS:
For regression coefficients and linear estimates, Bayes factors are
computed using the Savage–Dickey density ratio evaluated on the
marginal inference scale. Prior and posterior densities are Student’s
t distributions with shared degrees of freedom (df_t), reflecting
uncertainty in the residual variance under an empirical‑Bayes
approximation [3–5].
For residual correlations between outcomes, credible intervals are
computed on Fisher’s z [7] with effective degrees of freedom df_t and
then back‑transformed to r.
SUMMARY OF PRIORS:
The model employs the following priors for empirical Bayes inference:
o Intercept: Improper flat/Uniform prior, U(-Inf, Inf).
o Slopes: Marginal Student’s t prior on the coefficient (or estimate)
scale, t(0, sigma_prior, df_t), with scale determined by the
bootstrap‑optimised ridge parameter (lambda) and design effect
DEFF.
In the limit (high df_t), the inferential framework converges to a
Normal-Normal conjugate prior where the prior precision is
determined by the optimized lambda. At lower df_t, the function
provides more robust, t-marginalized inference to account for
uncertainty in the error variance.
o Residual Variance: Implicit (working) Inverse-Gamma prior,
Inv-Gamma(df_t/2, Sigma_Y_hat), induced by variance estimation
and marginalization and used to generate the t-layer.
o Correlations: An improper flat prior is assumed on Fisher’s z
transform of the correlation coefficients. Under this prior, the
posterior for z is proportional to the t‑based sampling distribution
implied by the effective degrees of freedom df_t.
UNCERTAINTY AND CLUSTERING:
The design effect specified by DEFF is integrated throughout the model
consistent with its definition:
DEFF(parameter) = Var_true(parameter) / Var_iid(parameter)
This guards against dependence between observations leading to anti-
conservative inference. This adjustment occurs at three levels:
1. Prior Learning: The ridge tuning constant (lambda) is selected by
minimizing predictive error on the i.i.d. bootstrap scale and then
divided by DEFF. This "dilutes" the prior precision, ensuring the
lambda_iid = sigma^2 / tau^2_iid
tau^2_true = DEFF * tau^2_iid
lambda_true = sigma^2 / tau^2_true = lambda_iid / DEFF
where sigma^2 (a.k.a. Sigma_Y_hat) is residual variance (data space)
and tau^2 (a.k.a. tau2_hat) is the prior variance (parameter space).
2. Scale Estimation: Residual variance (Sigma_Y_hat) is estimated using
the ridge-adjusted degrees of freedom (df_lambda = m - trace(H_lambda))
and is then inflated by a factor of DEFF. This yields an "effective"
noise scale on the derived parameter statistics that accounts for
within-cluster correlation [14, 15] according to:
Var_true(beta_hat) = DEFF * Var_iid(beta_hat)
3. Inferential Shape: A marginal Student’s t layer is used for all
quantiles and Bayes factors to propagate uncertainty in the
residual variance and effective sample size. To prevent over-
certainty in small-cluster settings, the inferential degrees of
freedom are reduced:
df_t = (m / DEFF) - trace (H_lambda), where m is size (Y, 1)
This ensures that both the scale (width) and the shape (tails) of the
posterior distributions are calibrated for the effective sample size.
The use of t‑based adjustments is akin to placing an Inverse-Gamma
prior (alpha = df_t / 2, beta = Sigma_Y_hat) on the residual variance
and is in line with classical variance component approximations (e.g.,
Satterthwaite/Kenward–Roger) and ridge inference recommendations
[16–18].
4. Stability Selection: The sign-consistency probabilities (denoted as
stability) under bootstrap resampling are adjusted for the design
effect via a Probit-link transformation:
Phi ( Phi^-1(stability) / sqrt (Deff) )
Where Phi and Phi^-1 are the cumulative standard normal distribution
function and its inverse respectively. This adjustment ensures that
the reported stability reflects the effective sample size rather than
the raw number of observations, preventing over-certainty in the
presence of clustered or dependent data.
ESTIMATING THE DESIGN EFFECT:
While DEFF = 1 + (g - 1) * r provides a useful analytical upper bound
based on cluster size (g) and intraclass correlation (r), the realized
impact of dependence on regression slopes often varies by predictor type.
For complex designs, DEFF is best estimated as the mean ratio of the
parameter variances—obtained from the variances of the bootstrap
distributions under a cluster-robust estimator (e.g., wild cluster
bootstrap via `bootwild` or cluster-based bayesian bootstrap via
`bootbayes`) relative to an i.i.d. assumption. Supplying this
"Effective DEFF" allows `bootridge` to provide analytical Bayesian
inference that approximates the results of a full hierarchical or
resampled model [14, 15].
DIAGNOSTIC ASSESSMENT:
Users should utilize `bootlm` for formal diagnostic plots (Normal
Q-Q, Spread-Location, Cook’s Distance). These tools identify
influential observations that may require inspection before or
after ridge fitting.
SUITABILITY:
This function is designed for models with continuous outcomes and
assumes a linear Normal (Gaussian) likelihood. It is not suitable for
binary, count, or categorical outcomes. However, binary and categorical
predictors are supported.
INTERNAL SCALING AND STANDARDIZATION:
All scaling and regularization procedures for optimizing the ridge
parameter are handled internally to ensure numerical stability and
balanced, scale-invariant shrinkage. To ensure all outcomes contribute
equally to the global regularization regardless of their units, the
ridge parameter (lambda) is optimized using internally standardized
outcomes.
When refitting the model with the optimal ridge parameter, while
predictors are maintained on their original scale, the ridge penalty
matrix is automatically constructed with diagonal elements proportional
to the column variances of X. This ensures that the shrinkage applied
to coefficients is equivalent to that of standardized predictors,
without requiring manual preprocessing (categorical terms are identified
via CATEGOR and are exempt from this variance-based penalty scaling).
Following optimization, the final model is refit to the outcomes on
their original scale; consequently, all posterior summaries,
credibility intervals, and prior standard deviations are reported
directly on the original coefficient scale for ease of interpretation.
STATISTICAL INFERENCE AND ERROR CONTROL:
Inference is provided via three complementary metrics: Credibility
Intervals (CI), Bayes Factors (BF), and Stability Selection (SS)
probabilities. Conditioned on a bootstrap-optimized ridge penalty, these
statistics exhibit superior control over Type M (magnitude) and Type S
(sign) errors relative to unpenalized estimators. The inherent shrinkage
provides implicit False Discovery Rate (FDR) control for CIs and BFs by
suppressing noise-driven inflation, providing more conservative global
error control than unpenalized methods. Conversely, SS probabilities
prioritize statistical power in sparse or low signal-to-noise ratio (SNR)
settings; while SS maintains marginal False Positive Rate (FPR) control
near ALPHA, it lacks the intrinsic FDR protection afforded by shrinkage
when interpreting multiple simultaneous inferences. The reliability of
all metrics improves as the Signal-to-Noise Ratio (SNR) increases.
CI BF SS
FDR-Controlled <----------------------------> FPR-Controlled
(High Stringency) (High Discovery)
See the last demo in this function for simulation code and results
supporting these claims.
See also: `bootstrp`, `boot`, `bootlm`, `bootbayes` and `bootwild`.
Bibliography:
[1] Delaney, N. J. & Chatterjee, S. (1986) Use of the Bootstrap and Cross-
Validation in Ridge Regression. Journal of Business & Economic Statistics,
4(2):255–262. https://doi.org/10.1080/07350015.1986.10509520
[2] Efron, B. & Tibshirani, R. J. (1993) An Introduction to the Bootstrap.
New York, NY: Chapman & Hall, pp. 247–252.
https://doi.org/10.1201/9780429246593
[3] Dickey, J. M. & Lientz, B. P. (1970) The Weighted Likelihood Ratio,
Sharp Hypotheses about Chances, the Order of a Markov Chain. Ann. Math.
Statist., 41(1):214–226. (Savage–Dickey)
https://doi.org/10.1214/aoms/1177697203
[4] Morris, C. N. (1983) Parametric Empirical Bayes Inference: Theory and
Applications. JASA, 78(381):47–55. https://doi.org/10.2307/2287098
[5] Wagenmakers, E.-J., Lodewyckx, T., Kuriyal, H., & Grasman, R. (2010)
Bayesian hypothesis testing for psychologists: A tutorial on the
Savage–Dickey method. Cognitive Psychology, 60(3):158–189.
https://doi.org/10.1016/j.cogpsych.2009.12.001
[6] Meinshausen, N. & Buhlmann, P. (2010) Stability selection. J. R. Statist.
Soc. B. 72(4): 417-473. https://doi.org/10.1111/j.1467-9868.2010.00740.x
[7] Fisher, R. A. (1921) On the "Probable Error" of a Coefficient of
Correlation Deduced from a Small Sample. Metron, 1:3–32. (Fisher z)
[8] Gelman, A., Hill, J., & Yajima, M. (2012) Why we usually don't worry
about multiple comparisons. J. Res. on Educ. Effectiveness, 5:189–211.
https://doi.org/10.1080/19345747.2011.618213
[9] Efron, B. (2010) Large-Scale Inference: Empirical Bayes Methods for
Estimation, Testing, and Prediction. Cambridge University Press.
https://doi.org/10.1017/CBO9780511761362
[10] Hastie, T., Tibshirani, R., & Friedman, J. (2009) The Elements of
Statistical Learning (2nd ed.). Springer.
https://doi.org/10.1007/978-0-387-84858-7
[11] Ye, J. (1998) On Measuring and Correcting the Effects of Data Mining and
Model Selection. JASA, 93(441):120–131. (Generalized df)
https://doi.org/10.1080/01621459.1998.10474094
[12] Akaike, H. (1973) Information Theory and an Extension of the Maximum
Likelihood Principle. In: 2nd Int. Symp. on Information Theory. (AIC/KL)
https://doi.org/10.1007/978-1-4612-0919-5_38
[13] Hoerl, A. E. & Kennard, R. W. (1970) Ridge Regression: Biased Estimation
for Nonorthogonal Problems. Technometrics, 12(1):55–67.
https://doi.org/10.1080/00401706.1970.10488634
[14] Neuhaus, J. M., & Segal, M. R. (1993). Design effects for binary
regression models fitted to dependent data. Statistics in Medicine,
12(13):1259–1268. https://doi.org/10.1002/sim.4780121309
[15] Cameron, A. C., & Miller, D. L. (2015) A Practitioner's Guide to
Cluster-Robust Inference. J. Hum. Resour., 50(2):317–372.
https://doi.org/10.3368/jhr.50.2.317
[16] Satterthwaite, F. E. (1946) An Approximate Distribution of Estimates of
Variance Components. Biometrics Bulletin, 2(6):110–114.
https://doi.org/10.2307/3002019
[17] Kenward, M. G. & Roger, J. H. (1997) Small Sample Inference for Fixed
Effects from Restricted Maximum Likelihood. Biometrics, 53(3):983–997.
https://doi.org/10.2307/2533558
[18] Vinod, H. D. (1987) Confidence Intervals for Ridge Regression Parameters.
In Time Series and Econometric Modelling, pp. 279–300.
https://doi.org/10.1007/978-94-009-4790-0_19
bootridge (version 2026.02.18)
Author: Andrew Charles Penn
Demonstration 1
The following code
% Analysis of Rohwer's dataset
% Data from an experiment by William D. Rohwer on kindergarten children
% designed to examine how well performance on a set of paired-associate (PA)
% tasks can predict performance on some measures of aptitude and achievement.
% Load the dataset
fid = fopen ('rohwer_data.csv', 'r', 'l');
dat = textscan ...
(fid, '%f %s %f %f %f %f %f %f %f %f', ...
'Delimiter', ',', 'HeaderLines', 1);
[group, SES, SAT, PPVT, Raven, n, s, ns, na, ss] = dat{:};
% Define model terms - all main effects and two-way interactions with SES
mdl = [1 0 0 0 0 0; ...
0 1 0 0 0 0; ...
0 0 1 0 0 0; ...
0 0 0 1 0 0; ...
0 0 0 0 1 0; ...
0 0 0 0 0 1; ...
1 1 0 0 0 0; ...
1 0 1 0 0 0; ...
1 0 0 1 0 0; ...
1 0 0 0 1 0; ...
1 0 0 0 0 1];
% Fit linear model with one of the outcomes to obtain design matrix
MAT = bootlm (SAT, {SES, n, s, ns, na, ss}, 'model', 'linear', ...
'nboot', 0, 'display', 'off', 'continuous', [2:6], ...
'contrasts', 'simple', 'model', mdl);
% Run machine learning optimized ridge regression with empirical bayes
% inference. By not assigning the output to a variable, we get results
% printed to stdout.
fprintf ('The bootridge function is running ...\n')
bootridge ([SAT, PPVT, Raven], MAT.X, 2, 200, .05);
% Get the output structure stored in ans from the last function call
S = ans;
Produces the following output
The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 11 Number of outcomes (q): 3 Sample size: 69 Design effect (Deff): 1 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 2.07996 Bootstrap optimized ridge tuning constant (lambda): 7.25059 Effective residual degrees of freedom (df_lambda): 59.3 Residual variances (range): [7.68, 564] Inferential degrees of freedom (df_t): 59.3 Used for credible intervals and Bayes factors below. 95% credible intervals for correlations between outcomes: (Prior on Fisher's z is flat/improper) Outcome J Outcome I correlation CI_lower CI_upper 1 2 +0.2149 -0.04599 +0.4484 1 3 +0.2957 +0.04040 +0.5147 2 3 +0.2968 +0.04166 +0.5156 95% credible intervals and Bayes factors for regression coefficients. Global ridge prior contribution to posterior precision: 20.77 % Stability selection (SS): >97.5% for the (-) or (+) sign of the coefficient. SS probabilities are reported in S.stability Outcome 1: coefficient CI_lower CI_upper lnBF10 SS prior +37.87 +31.77 +43.98 +NaN U (-Inf, Inf) +6.490 -3.554 +16.53 +0.275 t (0, 8.82, 59.3) +1.185 -0.7453 +3.115 -0.129 t (0, 2.34, 59.3) +1.113 -0.4437 +2.670 +0.0729 t (0, 2.01, 59.3) -2.441 -3.920 -0.9626 +4.31 (-) t (0, 1.61, 59.3) +2.127 +0.7229 +3.531 +3.64 (+) t (0, 1.42, 59.3) +0.8202 -0.5386 +2.179 -0.0338 t (0, 1.46, 59.3) +2.592 -1.316 +6.500 -0.0302 t (0, 4.87, 59.3) +2.241 -0.8743 +5.356 +0.0852 t (0, 4.03, 59.3) -2.339 -5.306 +0.6272 +0.460 t (0, 3.23, 59.3) +3.362 +0.5435 +6.179 +2.05 (+) t (0, 2.87, 59.3) -1.699 -4.450 +1.053 -0.0223 t (0, 3.02, 59.3) Outcome 2: coefficient CI_lower CI_upper lnBF10 SS prior +72.38 +69.54 +75.21 +NaN U (-Inf, Inf) +11.51 +6.840 +16.17 +9.81 (+) t (0, 4.10, 59.3) +0.2438 -0.6527 +1.140 -0.736 t (0, 1.09, 59.3) -0.1094 -0.8324 +0.6136 -0.903 t (0, 0.934, 59.3) -0.1821 -0.8689 +0.5047 -0.636 t (0, 0.748, 59.3) +1.126 +0.4736 +1.778 +4.82 (+) t (0, 0.658, 59.3) +0.5167 -0.1144 +1.148 +0.568 t (0, 0.679, 59.3) -0.1079 -1.923 +1.707 -0.905 t (0, 2.26, 59.3) +0.7991 -0.6477 +2.246 -0.335 t (0, 1.87, 59.3) +0.006221 -1.372 +1.384 -0.780 t (0, 1.50, 59.3) +0.09108 -1.218 +1.400 -0.701 t (0, 1.33, 59.3) +0.1488 -1.129 +1.427 -0.761 t (0, 1.40, 59.3) Outcome 3: coefficient CI_lower CI_upper lnBF10 SS prior +14.20 +13.48 +14.91 +NaN U (-Inf, Inf) +1.049 -0.1227 +2.221 +1.03 (+) t (0, 1.03, 59.3) +0.1118 -0.1134 +0.3371 -0.389 t (0, 0.273, 59.3) +0.2157 +0.03400 +0.3973 +1.79 (+) t (0, 0.235, 59.3) +0.03120 -0.1414 +0.2038 -0.712 t (0, 0.188, 59.3) +0.02972 -0.1341 +0.1935 -0.636 t (0, 0.165, 59.3) -0.03604 -0.1946 +0.1225 -0.662 t (0, 0.171, 59.3) -0.1310 -0.5871 +0.3251 -0.745 t (0, 0.568, 59.3) +0.3330 -0.03056 +0.6965 +0.711 (+) t (0, 0.470, 59.3) -0.2740 -0.6202 +0.07219 +0.469 t (0, 0.377, 59.3) +0.09246 -0.2364 +0.4213 -0.551 t (0, 0.335, 59.3) -0.04850 -0.3696 +0.2726 -0.742 t (0, 0.353, 59.3)
and the following figure
| Figure 1 |
|---|
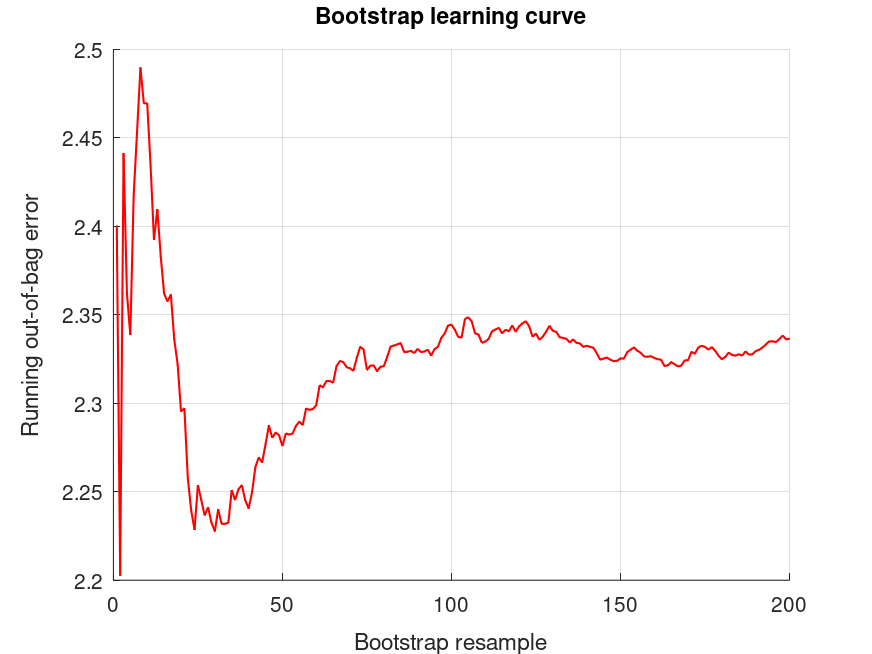 |
Demonstration 2
The following code
% Simple linear regression. The data represents salaries of employees and
% their years of experience, modified from Allena Venkata. The salaries are
% in units of 1000 dollars per annum.
years = [1.20 1.40 1.60 2.10 2.30 3.00 3.10 3.30 3.30 3.80 4.00 4.10 ...
4.10 4.20 4.60 5.00 5.20 5.40 6.00 6.10 6.90 7.20 8.00 8.30 ...
8.80 9.10 9.60 9.70 10.40 10.60]';
salary = [39 46 38 44 40 57 60 54 64 57 63 56 57 57 61 68 66 83 81 94 92 ...
98 101 114 109 106 117 113 122 122]';
fprintf ('The bootridge function is running ...\n')
bootridge (salary, years);
% We can see from the intercept that the starting starting salary is $25.2 K
% and that salary increase per year of experience is $9.4 K.
Produces the following output
The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 1 Number of outcomes (q): 1 Sample size: 30 Design effect (Deff): 1 Bootstrap resamples (nboot): 100 Minimized .632 bootstrap prediction error: 0.045731 Bootstrap optimized ridge tuning constant (lambda): 0.0767424 Effective residual degrees of freedom (df_lambda): 28.0 Residual variance (sigma^2): 32.8 Inferential degrees of freedom (df_t): 28.0 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for regression coefficients. Global ridge prior contribution to posterior precision: 0.26 % Stability selection (SS): >97.5% for the (-) or (+) sign of the coefficient. SS probabilities are reported in S.stability Outcome 1: coefficient CI_lower CI_upper lnBF10 SS prior +24.92 +20.25 +29.59 +NaN U (-Inf, Inf) +9.430 +8.663 +10.20 +42.9 (+) t (0, 7.29, 28.0)
and the following figure
| Figure 1 |
|---|
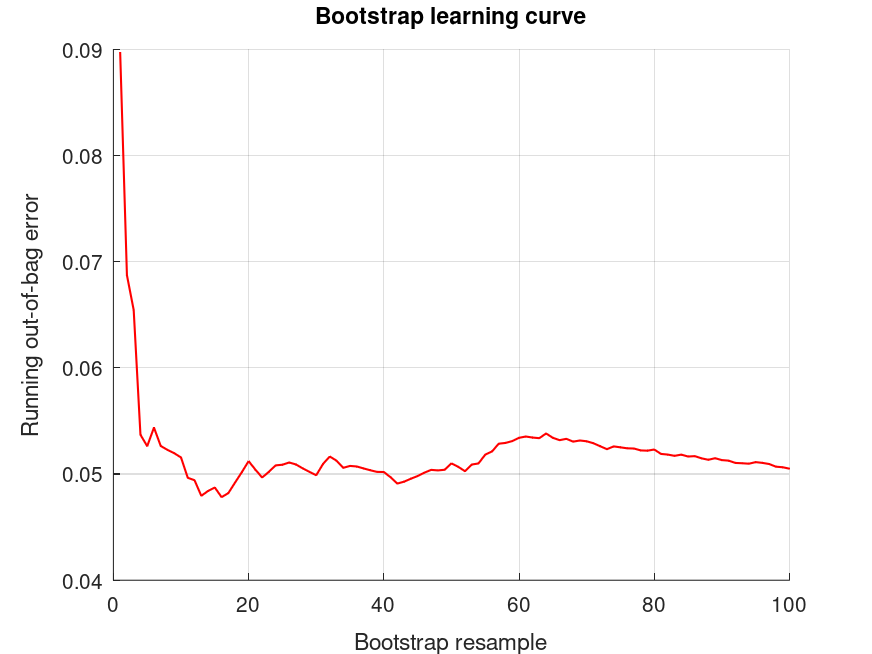 |
Demonstration 3
The following code
% Two-sample unpaired test on independent samples.
score = [54 23 45 54 45 43 34 65 77 46 65]';
gender = {'male' 'male' 'male' 'male' 'male' 'female' 'female' 'female' ...
'female' 'female' 'female'}';
% Difference between means
% Note that the 'dim' argument in `bootlm` automatically changes the default
% coding to simple contrasts, which are centered.
MAT = bootlm (score, gender, 'nboot', 0, 'display', 'off', ...
'dim', 1, 'posthoc', 'trt_vs_ctrl');
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, 2);
% Group means
MAT = bootlm (score, gender, 'nboot', 0, 'display', 'off', 'dim', 1);
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, 2, [], [], MAT.L);
Produces the following output
The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 1 Number of outcomes (q): 1 Sample size: 11 Design effect (Deff): 1 Bootstrap resamples (nboot): 100 Minimized .632 bootstrap prediction error: 1.04463 Bootstrap optimized ridge tuning constant (lambda): 2.58499 Effective residual degrees of freedom (df_lambda): 9.49 Residual variance (sigma^2): 218 Inferential degrees of freedom (df_t): 9.49 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for regression coefficients. Global ridge prior contribution to posterior precision: 48.66 % Stability selection (SS): >97.5% for the (-) or (+) sign of the coefficient. SS probabilities are reported in S.stability Outcome 1: coefficient CI_lower CI_upper lnBF10 SS prior +49.84 +39.83 +59.85 +NaN U (-Inf, Inf) +5.545 -8.834 +19.92 +0.0384 t (0, 9.18, 9.49) The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 1 Number of outcomes (q): 1 Sample size: 11 Design effect (Deff): 1 Bootstrap resamples (nboot): 100 Minimized .632 bootstrap prediction error: 1.04463 Bootstrap optimized ridge tuning constant (lambda): 2.58499 Effective residual degrees of freedom (df_lambda): 9.49 Residual variance (sigma^2): 218 Inferential degrees of freedom (df_t): 9.49 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for linear estimates. Global ridge prior contribution to posterior precision: 48.66 % Outcome 1: estimate CI_lower CI_upper lnBF10 prior +47.07 +34.36 +59.77 +NaN U (-Inf, Inf) +52.61 +40.67 +64.55 +NaN U (-Inf, Inf)
and the following figure
| Figure 1 |
|---|
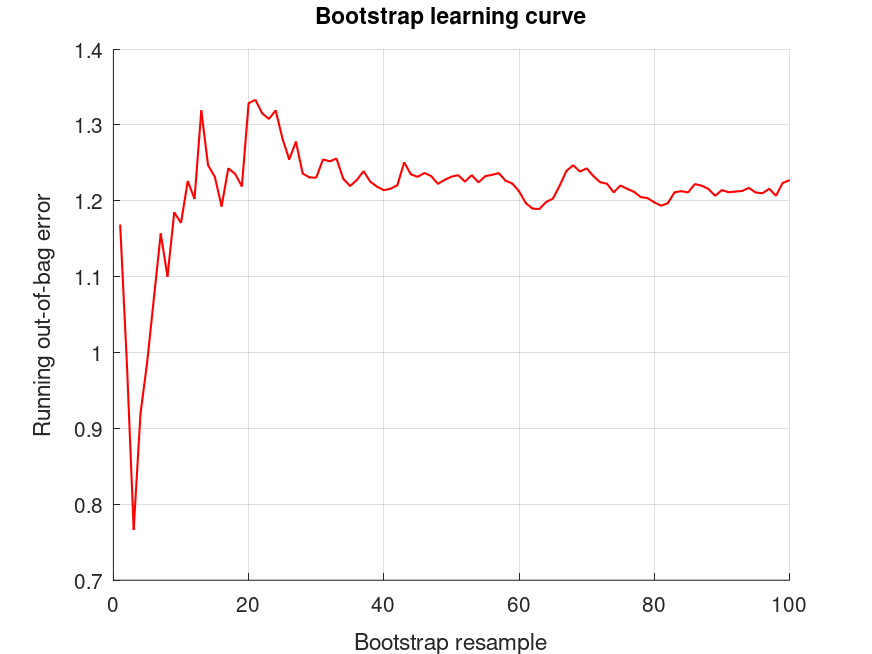 |
Demonstration 4
The following code
% One-way repeated measures design.
% The data is from a study on the number of words recalled by 10 subjects
% for three time condtions, in Loftus & Masson (1994) Psychon Bull Rev.
% 1(4):476-490, Table 2.
words = [10 13 13; 6 8 8; 11 14 14; 22 23 25; 16 18 20; ...
15 17 17; 1 1 4; 12 15 17; 9 12 12; 8 9 12];
seconds = [1 2 5; 1 2 5; 1 2 5; 1 2 5; 1 2 5; ...
1 2 5; 1 2 5; 1 2 5; 1 2 5; 1 2 5;];
subject = [ 1 1 1; 2 2 2; 3 3 3; 4 4 4; 5 5 5; ...
6 6 6; 7 7 7; 8 8 8; 9 9 9; 10 10 10];
% Frequentist framework: wild bootstrap of linear model, with orthogonal
% polynomial contrast coding followed up with treatment vs control
% hypothesis testing.
MAT = bootlm (words, {subject,seconds}, 'display', 'off', 'varnames', ...
{'subject','seconds'}, 'model', 'linear', 'contrasts', ...
'poly', 'dim', 2, 'posthoc', 'trt_vs_ctrl', 'nboot', 0);
% Ridge regression and bayesian analysis of posthoc comparisons
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, '*', 200, 0.05, MAT.L);
% Frequentist framework: wild bootstrap of linear model, with orthogonal
% polynomial contrast coding followed up estimating marginal means.
MAT = bootlm (words, {subject,seconds}, 'display', 'off', 'nboot', 0, ...
'model', 'linear', 'contrasts', 'poly', 'dim', 2);
% Ridge regression and bayesian analysis of model estimates. Note that group-
% mean Bayes Factors are NaN under the flat prior on the intercept whereas
% the contrasts we just calculated had proper Normal priors.
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, '*', 200, 0.05, MAT.L);
Produces the following output
The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 11 Number of outcomes (q): 1 Sample size: 30 Design effect (Deff): 1 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 0.117537 Bootstrap optimized ridge tuning constant (lambda): 0.028454 Effective residual degrees of freedom (df_lambda): 18.1 Residual variance (sigma^2): 0.616 Inferential degrees of freedom (df_t): 18.1 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for linear estimates. Global ridge prior contribution to posterior precision: 0.82 % Outcome 1: estimate CI_lower CI_upper lnBF10 prior +1.994 +1.258 +2.731 +6.86 t (0, 6.58, 18.1) +3.191 +2.455 +3.927 +13.5 t (0, 6.58, 18.1) The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 11 Number of outcomes (q): 1 Sample size: 30 Design effect (Deff): 1 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 0.117537 Bootstrap optimized ridge tuning constant (lambda): 0.028454 Effective residual degrees of freedom (df_lambda): 18.1 Residual variance (sigma^2): 0.616 Inferential degrees of freedom (df_t): 18.1 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for linear estimates. Global ridge prior contribution to posterior precision: 0.82 % Outcome 1: estimate CI_lower CI_upper lnBF10 prior +11.00 +10.48 +11.53 +NaN U (-Inf, Inf) +13.00 +12.48 +13.52 +NaN U (-Inf, Inf) +14.20 +13.67 +14.72 +NaN U (-Inf, Inf)
and the following figure
| Figure 1 |
|---|
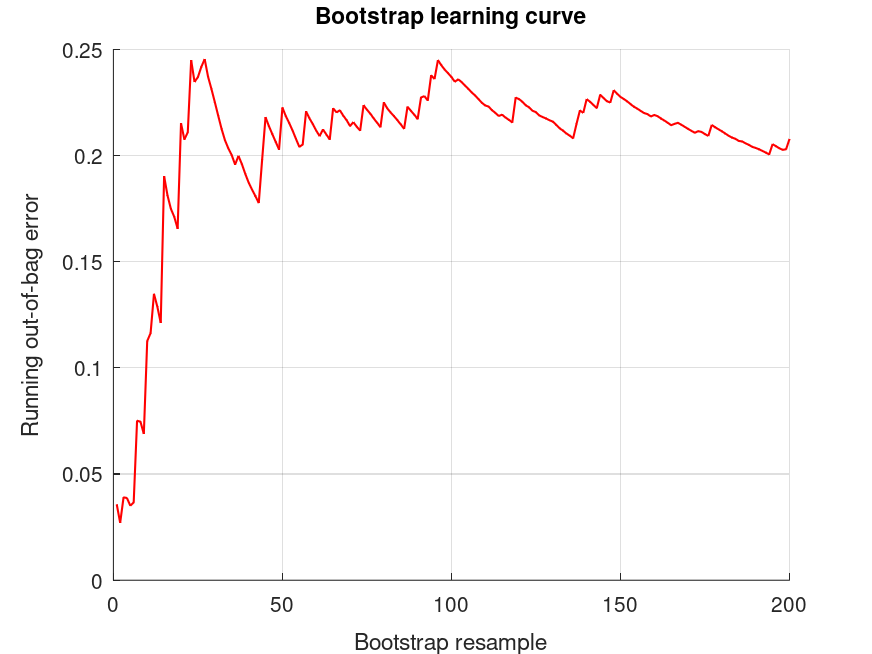 |
Demonstration 5
The following code
% One-way design with continuous covariate. The data is from a study of the
% additive effects of species and temperature on chirpy pulses of crickets,
% from Stitch, The Worst Stats Text eveR
pulse = [67.9 65.1 77.3 78.7 79.4 80.4 85.8 86.6 87.5 89.1 ...
98.6 100.8 99.3 101.7 44.3 47.2 47.6 49.6 50.3 51.8 ...
60 58.5 58.9 60.7 69.8 70.9 76.2 76.1 77 77.7 84.7]';
temp = [20.8 20.8 24 24 24 24 26.2 26.2 26.2 26.2 28.4 ...
29 30.4 30.4 17.2 18.3 18.3 18.3 18.9 18.9 20.4 ...
21 21 22.1 23.5 24.2 25.9 26.5 26.5 26.5 28.6]';
species = {'ex' 'ex' 'ex' 'ex' 'ex' 'ex' 'ex' 'ex' 'ex' 'ex' 'ex' ...
'ex' 'ex' 'ex' 'niv' 'niv' 'niv' 'niv' 'niv' 'niv' 'niv' ...
'niv' 'niv' 'niv' 'niv' 'niv' 'niv' 'niv' 'niv' 'niv' 'niv'};
% Estimate regression coefficients using 'anova' contrast coding
MAT = bootlm (pulse, {temp, species}, 'model', 'linear', ...
'continuous', 1, 'display', 'off', ...
'contrasts', 'anova', 'nboot', 0);
% Ridge regression and bayesian analysis of regression coefficients
% MAT.X: column 1 is intercept, column 2 is temp (continuous), column 3
% is species (categorical).
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, 3, 200, 0.05);
Produces the following output
The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 2 Number of outcomes (q): 1 Sample size: 31 Design effect (Deff): 1 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 0.0122387 Bootstrap optimized ridge tuning constant (lambda): 0.0310279 Effective residual degrees of freedom (df_lambda): 28.0 Residual variance (sigma^2): 3.19 Inferential degrees of freedom (df_t): 28.0 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for regression coefficients. Global ridge prior contribution to posterior precision: 0.33 % Stability selection (SS): >97.5% for the (-) or (+) sign of the coefficient. SS probabilities are reported in S.stability Outcome 1: coefficient CI_lower CI_upper lnBF10 SS prior +73.37 +72.71 +74.03 +NaN U (-Inf, Inf) +3.601 +3.402 +3.800 +53.4 (+) t (0, 2.65, 28.0) -10.03 -11.53 -8.528 +26.9 (-) t (0, 10.1, 28.0)
and the following figure
| Figure 1 |
|---|
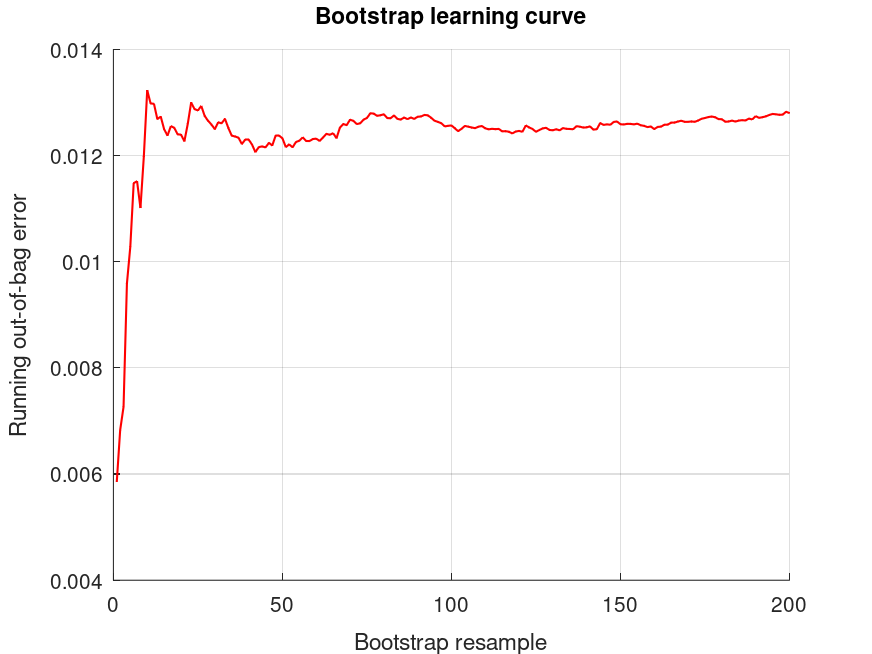 |
Demonstration 6
The following code
% Variations in design for two-way ANOVA (2x2) with interaction.
% Arousal was measured in rodents assigned to four experimental groups in a
% between-subjects design with two factors: group (lesion/control) and
% stimulus (fearful/neutral). In this design, each rodent is allocated to one
% combination of levels in group and stimulus, and a single measurment of
% arousal is made. The question we are asking here is, does the effect of a
% fear-inducing stimulus on arousal depend on whether or not rodents had a
% lesion?
group = {'control' 'control' 'control' 'control' 'control' 'control' ...
'lesion' 'lesion' 'lesion' 'lesion' 'lesion' 'lesion' ...
'control' 'control' 'control' 'control' 'control' 'control' ...
'lesion' 'lesion' 'lesion' 'lesion' 'lesion' 'lesion'};
stimulus = {'fearful' 'fearful' 'fearful' 'fearful' 'fearful' 'fearful' ...
'fearful' 'fearful' 'fearful' 'fearful' 'fearful' 'fearful' ...
'neutral' 'neutral' 'neutral' 'neutral' 'neutral' 'neutral' ...
'neutral' 'neutral' 'neutral' 'neutral' 'neutral' 'neutral'};
arousal = [0.78 0.86 0.65 0.83 0.78 0.81 0.65 0.69 0.61 0.65 0.59 0.64 ...
0.54 0.6 0.67 0.63 0.56 0.55 0.645 0.565 0.625 0.485 0.655 0.515];
% Fit between-subjects design
[STATS, BOOTSTAT, AOVSTAT, PRED_ERR, MAT] = bootlm (arousal, ...
{group, stimulus}, 'seed', 1, ...
'display', 'off', 'contrasts', 'simple', ...
'model', 'full', ...
'method', 'bayes');
% Ridge regression and bayesian analysis of regression coefficients
% MAT.X: column 1 is intercept, column 2 is temp (continuous), column 3
% is species (categorical).
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, '*', 200, 0.05);
% Now imagine the design is repeated stimulus measurements in each rodent
ID = [1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12]';
% Fit model including ID as a blocking-factor
MAT = bootlm (arousal, {ID, group, stimulus}, 'seed', 1, 'nboot', 0, ...
'display', 'off', 'contrasts', 'simple', 'method', 'bayes', ...
'model', [1 0 0; 0 1 0; 0 0 1; 0 1 1]);
% Ridge regression and bayesian analysis of regression coefficients
% MAT.X: column 1 is intercept, column 2 is temp (continuous), column 3
% is species (categorical).
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, '*', 200, 0.05);
Produces the following output
The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 3 Number of outcomes (q): 1 Sample size: 24 Design effect (Deff): 1 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 0.41427 Bootstrap optimized ridge tuning constant (lambda): 0.305249 Effective residual degrees of freedom (df_lambda): 20.3 Residual variance (sigma^2): 0.00356 Inferential degrees of freedom (df_t): 20.3 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for regression coefficients. Global ridge prior contribution to posterior precision: 8.86 % Stability selection (SS): >97.5% for the (-) or (+) sign of the coefficient. SS probabilities are reported in S.stability Outcome 1: coefficient CI_lower CI_upper lnBF10 SS prior +0.6492 +0.6238 +0.6746 +NaN U (-Inf, Inf) -0.07454 -0.1241 -0.02501 +2.69 (-) t (0, 0.108, 20.3) -0.1189 -0.1685 -0.06942 +7.04 (-) t (0, 0.108, 20.3) +0.1136 +0.02100 +0.2061 +2.08 (+) t (0, 0.108, 20.3) The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 14 Number of outcomes (q): 1 Sample size: 24 Design effect (Deff): 1 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 0.541584 Bootstrap optimized ridge tuning constant (lambda): 1.34378 Effective residual degrees of freedom (df_lambda): 15.2 Residual variance (sigma^2): 0.00422 Inferential degrees of freedom (df_t): 15.2 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for regression coefficients. Global ridge prior contribution to posterior precision: 40.29 % Stability selection (SS): >97.5% for the (-) or (+) sign of the coefficient. SS probabilities are reported in S.stability Outcome 1: coefficient CI_lower CI_upper lnBF10 SS prior +0.6492 +0.6209 +0.6774 +NaN U (-Inf, Inf) +0.03475 -0.04703 +0.1165 +0.0470 t (0, 0.0561, 15.2) -0.007114 -0.08890 +0.07467 -0.359 t (0, 0.0561, 15.2) +0.03475 -0.04703 +0.1165 +0.0470 t (0, 0.0561, 15.2) -0.001133 -0.08292 +0.08065 -0.377 t (0, 0.0561, 15.2) +0.004848 -0.07694 +0.08663 -0.369 t (0, 0.0561, 15.2) +0.01436 -0.06856 +0.09729 -0.292 t (0, 0.0561, 15.2) +0.002400 -0.08053 +0.08533 -0.362 t (0, 0.0561, 15.2) -0.003582 -0.08651 +0.07934 -0.359 t (0, 0.0561, 15.2) -0.03349 -0.1164 +0.04944 +0.0206 t (0, 0.0561, 15.2) -0.0005911 -0.08352 +0.08233 -0.364 t (0, 0.0561, 15.2) -0.02751 -0.1104 +0.05542 -0.102 t (0, 0.0561, 15.2) -0.04841 -0.1174 +0.02057 +0.562 (-) t (0, 0.0561, 15.2) -0.1021 -0.1532 -0.05109 +5.52 (-) t (0, 0.0561, 15.2) +0.07209 -0.009930 +0.1541 +1.30 (+) t (0, 0.0561, 15.2)
and the following figure
| Figure 1 |
|---|
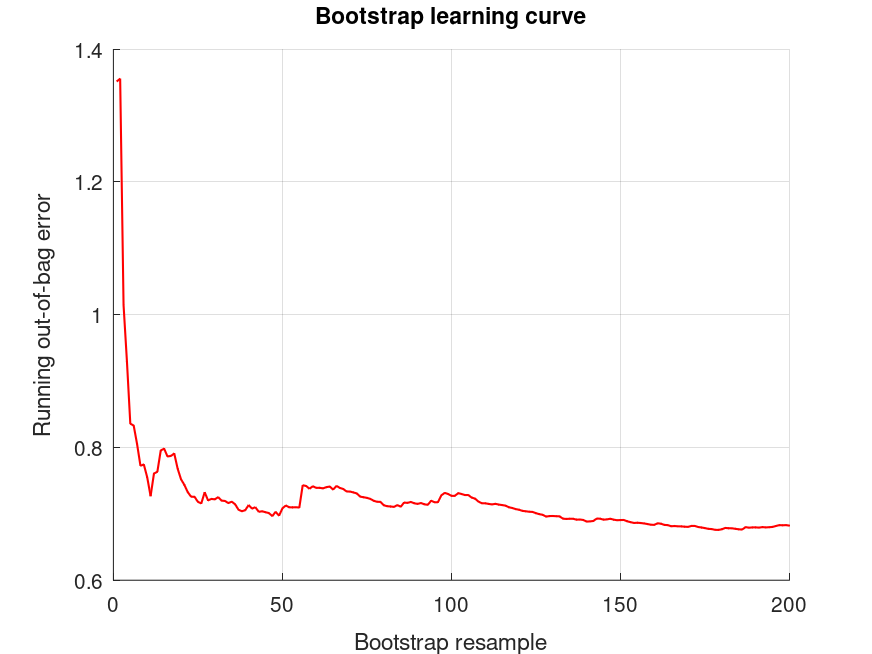 |
Demonstration 7
The following code
% Analysis of nested one-way design.
% Nested model example from:
% https://www.southampton.ac.uk/~cpd/anovas/datasets/#Chapter2
data = [4.5924 7.3809 21.322; -0.5488 9.2085 25.0426; ...
6.1605 13.1147 22.66; 2.3374 15.2654 24.1283; ...
5.1873 12.4188 16.5927; 3.3579 14.3951 10.2129; ...
6.3092 8.5986 9.8934; 3.2831 3.4945 10.0203];
clustid = [1 3 5; 1 3 5; 1 3 5; 1 3 5; ...
2 4 6; 2 4 6; 2 4 6; 2 4 6];
group = {'A' 'B' 'C'; 'A' 'B' 'C'; 'A' 'B' 'C'; 'A' 'B' 'C'; ...
'A' 'B' 'C'; 'A' 'B' 'C'; 'A' 'B' 'C'; 'A' 'B' 'C'};
% Fit model with cluster-based resampling. We are using Bayesian bootstrap
% using 'auto' prior, which effectively applies Bessel's correction to the
% variance of the bootstrap distribution for the contrasts (trt_vs_ctrl).
% Use 'treatment' coding and return regression coefficients since our
% intention is to use the posterior distributions from bayesian bootstrap
% to calculate the design effect.
[STATS, BOOTSTAT, AOVSTAT, PREDERR, MAT] = bootlm (data, {group}, ...
'clustid', clustid, 'seed', 1, 'display', 'off', 'contrasts', ...
'treatment', 'method', 'bayes', 'prior', 'auto');
% Or we can get a obtain the design effect empirically using resampling.
% We already fit the model accounting for clustering, now lets fit it
% under I.I.D. (i.e. without clustering). As above, use 'treatment' coding.
[STATS_SRS, BOOTSTAT_SRS] = bootlm (data, {group}, 'seed', 1, 'display', ...
'off', 'contrasts', 'treatment', 'method', 'bayes');
% Empirically calculate the design effect averaged over the variance of
% of the contrasts we are interested in
Var_true = var (BOOTSTAT, 0, 2);
Var_iid = var (BOOTSTAT_SRS, 0, 2);
DEFF = mean (Var_true ./ Var_iid);
% Or more simply, we can use the deffcalc function, which does the same thing.
% We take the mean DEFF across all contrasts for a stable global penalty.
DEFF = mean (deffcalc (BOOTSTAT, BOOTSTAT_SRS))
% Refit the model using orthogonal (helmert) contrasts and a hypothesis
% matrix specifying pairwise comparisons. Set nboot to 0 to avoid resampling.
MAT = bootlm (data, {group}, 'clustid', clustid, 'display', 'off', ...
'contrasts', 'helmert', 'dim', 1, 'posthoc', 'pairwise', ...
'nboot', 0);
% Fit a cluster-robust empirical Bayes model using our bootstrap estimate of
% the design effect and using the hypothesis matrix to define the comparisons
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, '*', 200, 0.05, MAT.L, DEFF);
% Compare this to using a maximum cluster size as an upperbound for Deff
g = max (accumarray (clustid(:), 1, [], @sum)); % g is max. cluster size
fprintf ('The bootridge function is running ...\n')
bootridge (MAT.Y, MAT.X, '*', 200, 0.05, MAT.L, g); % Upperbound DEFF is g
% Note: Using the empirical DEFF (~1.5) instead of the upper-bound (4.0)
% recovers inferential power, as seen by the higher Bayes Factor (lnBF10)
% and narrower credible intervals.
Produces the following output
DEFF = 1.4556 The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 2 Number of outcomes (q): 1 Sample size: 24 Design effect (Deff): 1.46 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 0.463286 Bootstrap optimized ridge tuning constant (lambda, Deff-adjusted): 0.318356 Effective residual degrees of freedom (df_lambda): 21.1 Residual variance (sigma^2, Deff-inflated): 31.8 Inferential degrees of freedom (df_t, Deff-adjusted): 13.6 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for linear estimates. Global ridge prior contribution to posterior precision: 6.50 % Outcome 1: estimate CI_lower CI_upper lnBF10 prior -6.336 -12.21 -0.4634 +1.03 t (0, 11.2, 13.6) -12.82 -18.69 -6.947 +5.63 t (0, 11.2, 13.6) -6.483 -12.32 -0.6518 +1.26 t (0, 9.99, 13.6) The bootridge function is running ... Empirical Bayes Ridge Regression (.632 Bootstrap Tuning) - Summary ******************************************************************************* Number of predictors (p): 2 Number of outcomes (q): 1 Sample size: 24 Design effect (Deff): 4 Bootstrap resamples (nboot): 200 Minimized .632 bootstrap prediction error: 0.463286 Bootstrap optimized ridge tuning constant (lambda, Deff-adjusted): 0.115848 Effective residual degrees of freedom (df_lambda): 21.0 Residual variance (sigma^2, Deff-inflated): 87.1 Inferential degrees of freedom (df_t, Deff-adjusted): 3.05 Used for credible intervals and Bayes factors below. 95% credible intervals and Bayes factors for linear estimates. Global ridge prior contribution to posterior precision: 2.47 % Outcome 1: estimate CI_lower CI_upper lnBF10 prior -6.532 -21.08 +8.017 -0.871 t (0, 30.7, 3.05) -13.33 -27.88 +1.214 +0.776 t (0, 30.7, 3.05) -6.802 -21.31 +7.708 -0.691 t (0, 27.4, 3.05)
and the following figure
| Figure 1 |
|---|
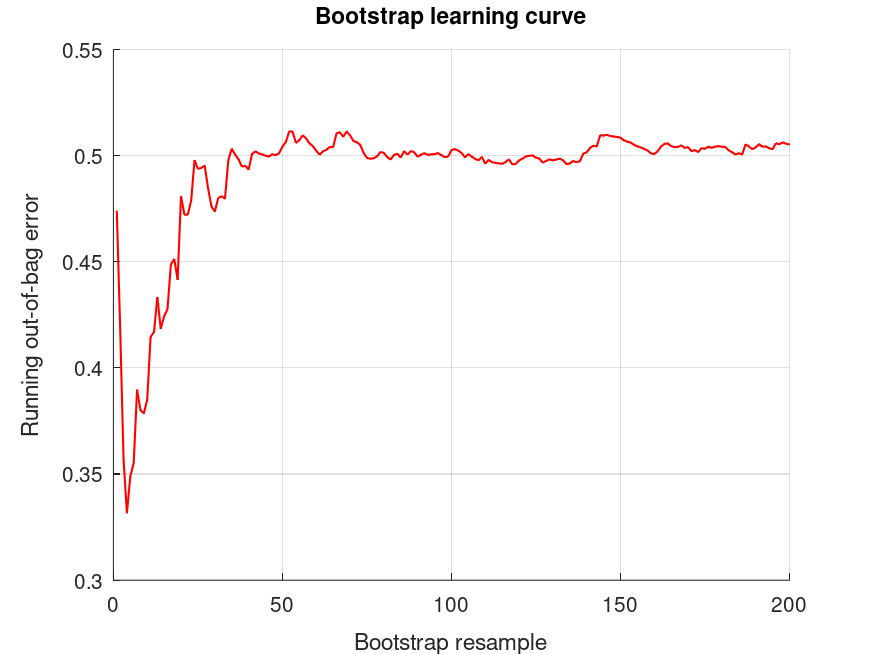 |
Demonstration 8
The following code
%% --- Stress-test: Simulated Large-Scale Patch-seq Project (bootridge) ---
%% N = 7500 cells
%% p = 15 features
%% q = 2000 genes
%% This tests memory handling and global lambda optimization.
N = 7500;
p = 15;
q = 2000;
nboot = 100;
% Set random seeds for the simulation
rand ('seed', 123);
randn ('seed', 123);
fprintf ('Simulate Large-Scale Patch-seq Dataset (%d x %d)...\n', N, q);
% Generate design matrix X (E-phys features)
X = [ones(N,1), randn(N, p-1)];
% Generate sparse multivariate outcome Y (Gene expression)
% Approx 120MB of data
true_beta = randn (p, q) .* (rand (p, q) > 0.9);
% Set signal-to-noise ratio to 0.5
target_snr = 0.5;
beta_no_intercept = true_beta(2:end, :);
signal_var_per_gene = sum (beta_no_intercept.^2, 1);
snr_per_gene = signal_var_per_gene / (0.5^2);
current_snr = mean (snr_per_gene);
scale = sqrt (target_snr / current_snr);
true_beta(2:end, :) = true_beta(2:end, :) * scale;
% Introduce correlations
n_factors = 10; % 10 latent biological processes
latent_X = randn (N, n_factors);
% Each latent factor affects about 10% of genes (sparse correlation)
latent_beta = randn (n_factors, q) .* (rand (n_factors, q) > 0.90);
% Simulate the data with added correlated noise (0.2 strength)
Y = X * true_beta + (latent_X * latent_beta * 0.2) + randn (N, q) * 0.5;
fprintf('Running bootridge ...\n');
tic;
% Use TOL = 0.05 for faster convergence in demo
S = bootridge (Y, X, [], nboot, 0.05, [], 1, 123, 0.05);
runtime = toc;
fprintf ('\n--- Performance Results ---\n');
fprintf ('Runtime: %.2f seconds\n', runtime);
fprintf ('Optimized Lambda: %.6f\n', S.lambda);
fprintf ('Total Iterations: %d\n', S.iter);
% Accuracy Check on a random gene
target_gene = ceil (rand * q);
estimated = S.coefficient(:, target_gene);
actual = true_beta(:, target_gene);
correlation = corr (estimated, actual);
% ROC statistics
threshold = 3; % corresponds to BF10 of 20
fp = sum (S.lnBF10(true_beta == 0) > threshold); % false positives
tp = sum (S.lnBF10(true_beta ~= 0) > threshold); % true positives
fn = sum (S.lnBF10(true_beta ~= 0) <= threshold); % missed true effects
power = tp / (tp + fn); % true positive rate
fp_rate = fp / sum (true_beta(:) == 0); % false positive rate
precision = tp / (tp + fp); % true discovery rate
fprintf ('Correlation of estimates for Gene %d: %.4f\n', ...
target_gene, correlation);
fprintf ('Number of coefficients: [%s] (Expected: [15 x 2000])\n', ...
num2str (size (S.coefficient)));
fprintf ('Number of pairwise correlations: [%s] (Expected: 1999000)\n', ...
num2str (size (S.RTAB, 1)));
fprintf ('Positive detections (i.e. discoveries) defined hereon as BF10 > 20');
fprintf ('\nFalse positive rate (FPR): %.1f%%\n', fp_rate * 100);
fprintf ('Precision (i.e. 1-FDR): %.1f%%\n', precision * 100);
fprintf ('Power (i.e. TPR): %.1f%%\n', power * 100);
Produces the following output
Simulate Large-Scale Patch-seq Dataset (7500 x 2000)... Running bootridge ... --- Performance Results --- Runtime: 916.49 seconds Optimized Lambda: 65.132264 Total Iterations: 12 Correlation of estimates for Gene 158: 0.9952 Number of coefficients: [15 2000] (Expected: [15 x 2000]) Number of pairwise correlations: [1999000] (Expected: 1999000) Positive detections (i.e. discoveries) defined hereon as BF10 > 20 False positive rate (FPR): 0.1% Precision (i.e. 1-FDR): 98.9% Power (i.e. TPR): 94.8%
Demonstration 9
The following code
%% --- Stress-test: Large-Scale Differential Gene Expression (DGE) Simulation ---
%% Scenario: Bulk RNA-seq Case-Control Study (e.g., Disease vs. Healthy)
%% N = 300 samples (e.g., 150 Patient / 150 Control)
%% p = 50 covariates (e.g., 1 Group Indicator + 49 Technical/PEER factors)
%% q = 15000 genes (Simultaneously modeled outcomes)
%%
%% This demo evaluates the multivariate efficiency of bootridge across
%% the typical protein-coding transcriptome size, testing memory handling
%% and the speed of global lambda optimization.
% 1. Setup Dimensions
N = 300; % Total biological samples (Bulk RNA-seq)
p = 50; % 1 Experimental Group + technical covariates (Age, RIN, Batch)
q = 15000; % Total Genes analyzed in this "chunk"
nboot = 100; % Number of bootstrap resamples
% Set random seeds for the simulation
rand ('seed', 123);
randn ('seed', 123);
fprintf (cat (2, 'Simulating DGE Dataset: %d samples, %d genes, %d ', ...
'covariates...\n'), N, q, p);
% 2. Generate Design Matrix X
% Column 1: Intercept
% Column 2: Group Indicator (0 = Control, 1 = Case)
% Columns 3-p: Random technical noise (Covariates/PEER factors)
Group = [zeros(N/2, 1); ones(N/2, 1)];
Covariates = randn (N, p-2);
X = [ones(N, 1), Group, Covariates];
% 3. Define Biological Signal (The "True" Log-Fold Changes)
% We simulate a realistic DGE profile:
% 10% of genes are differentially expressed (hits).
true_beta = zeros (p, q);
sig_genes = ceil (rand (1, round (q * 0.10)) * q);
true_beta(2, sig_genes) = (randn (1, length (sig_genes)) * 2); % Group effect
% 4. Generate Expression Matrix Y (Log2 TPM / Counts)
% Baseline + Group Effect + Gaussian noise.
Baseline = 5 + randn (1, q);
Y = repmat (Baseline, N, 1) + X * true_beta + randn (N, q) * 1.2;
fprintf ('Running Multivariate bootridge (Shrinkage shared across genes)...\n');
tic;
% CATEGOR = 2: Treats the Group column as categorical (no variance scaling).
% SEED = 123: Ensures reproducible bootstrap sampling.
% TOL = 0.05: Convergence tolerance for the golden section search.
S = bootridge (Y, X, 2, nboot, 0.05, [], 1, 123, 0.05);
runtime = toc;
% 5. Display Performance Results
fprintf ('\n--- Performance Results ---\n');
fprintf ('Runtime: %.2f seconds\n', runtime);
fprintf ('Optimized Lambda: %.6f\n', S.lambda);
% 6. Accuracy Check
% Compare estimated Beta (Group Effect) against the Ground Truth Fold-Changes
estimated_fc = S.coefficient(2, :);
true_fc = true_beta(2, :);
correlation = corr (estimated_fc', true_fc');
fprintf ('Correlation of Fold-Changes across %d genes: %.4f\n', ...
q, correlation);
fprintf ('Number of coefficients: [%s] (Expected: [50 x 15000])\n', ...
num2str (size (S.coefficient)));
fprintf ('Number of pairwise correlations: [%s] (Expected: 112492500)\n', ...
num2str (size (S.RTAB, 1)));
Produces the following output
Simulating DGE Dataset: 300 samples, 15000 genes, 50 covariates... Running Multivariate bootridge (Shrinkage shared across genes)... --- Performance Results --- Runtime: 515.46 seconds Optimized Lambda: 510.212731 Correlation of Fold-Changes across 15000 genes: 0.9759 Number of coefficients: [50 15000] (Expected: [50 x 15000]) Number of pairwise correlations: [112492500] (Expected: 112492500)
Demonstration 10
The following code
%% --- Stress-test: High-p Voxel-wise Neural Encoding Simulation ---
%% Scenario: Reconstructing Visual Stimuli from fMRI BOLD signals
%% N = 500 volumes (samples), p = 8000 voxels, q = 1 stimulus feature
%% This demo requires the signal package in octave
% 1. Setup Dimensions
N = 500; p = 8000; q = 1; nboot = 200;
rand ('seed', 123); randn ('seed', 123);
fprintf('Simulating fMRI Encoding: %d timepoints, %d voxels...\n', N, p);
% 2. Generate Design Matrix X (The Voxels)
% Spatial correlation between voxels (columns) and time points (rows)
X_raw = randn (N, p-1);
X = [ones(N, 1), filter([0.5 1 0.5], 1, X_raw, [], 2)];
X(:,2:end) = filter ([0.1, 0.4, 0.9, 1, 0.6, 0.2], 1, X(:,2:end), [], 1);
% 3. Define the "Neural Code" (True Weights)
true_beta_sparse = zeros (p, q); % Initialise
active_voxels = 1 + ceil (rand (1, 25) * (p - 1)); % 50 spatial clusters
true_beta_sparse(active_voxels) = randn (25, 1) * 100; % Active voxels
kernel = [0.05 0.1 0.4 0.8 1 0.8 0.4 0.1 0.05]; % Smoothing kernel
true_beta = filter (kernel, 1, true_beta_sparse); % Smooth active voxels
% 4. Generate outcome Y (The Stimulus)
% Signal from smoothed clusters + Gaussian noise
Y = X * true_beta + randn (N, q);
% 5. Estimate Design Effect (Deff) to account for serial dependence
% We use the autocorrelation of Y to estimate the variance inflation factor
%
% Bayley, G. V., & Hammersley, J. M. (1946). The "Effective" Number of
% Independent Observations in an Autocorrelated Time Series. Supplement to
% the Journal of the Royal Statistical Society, 8(2), 184–197.
% https://doi.org/10.2307/2983560
try
info = ver;
isoctave = any (ismember ({info.Name}, 'Octave'));
if (isoctave)
pkg load signal;
end
[r, lags] = xcov (Y - mean (Y), 10, 'coeff');
Deff = 1 + 2 * sum (r(lags > 0));
fprintf ('Estimated Design Effect (Deff): %.3f\n', Deff);
catch
Deff = 1;
end
% 6. Run bootridge
fprintf ('Running bootridge (Global Lambda Optimization)...\n');
tic;
% Run the bootridge function
S = bootridge (Y, X, [], nboot, 0.05, [], Deff, 123, 0.05);
runtime = toc;
% 7. Performance Results
estimated_beta = S.coefficient;
correlation = corr (estimated_beta, true_beta);
fprintf ('\n--- Performance Results ---\n');
fprintf ('Runtime: %.2f seconds\n', runtime);
fprintf ('Optimized Lambda: %.6f\n', S.lambda);
fprintf ('Correlation of Voxel Weight Map: %.4f\n', correlation);
fprintf ('Number of coefficients: [%s] (Expected: [8000 x 1])\n', ...
num2str (size (S.coefficient)));
Produces the following output
Simulating fMRI Encoding: 500 timepoints, 8000 voxels... Estimated Design Effect (Deff): 3.489 Running bootridge (Global Lambda Optimization)... Note: t-statistics evaluated with effective degrees of freedom clamped at 1 degree of freedom. --- Performance Results --- Runtime: 4958.29 seconds Optimized Lambda: 0.326447 Correlation of Voxel Weight Map: 0.3970 Number of coefficients: [8000 1] (Expected: [8000 x 1])
Demonstration 11
The following code
% Error Control: Global Ridge vs Per-Outcome Wild Bootstrap (n = 40)
% under global multicollinearity (r = 0.2)
%
% --- Parameters ---
% n_sims = 30;
% alpha = 0.05;
% n_vals = 40;
% p_vals = [3, 10, 30];
% q_vals = [1, 5, 10];
% snr_vals = [0.1, 0.2, 0.4, 0.8];
% seed = 42;
% randn('seed', seed);
%
% for p = p_vals
% for q = q_vals
% for snr = snr_vals
% % Accumulators
% fpr_r_ci = 0; fpr_r_bf = 0; fpr_r_ss = 0;
% fpr_w_std = 0; fpr_w_max = 0;
% fdr_r_ci = 0; fdr_r_bf = 0; fdr_r_ss = 0;
% fdr_w_std = 0; fdr_w_max = 0;
% pow_r_ci = 0; pow_r_bf = 0; pow_r_ss = 0;
% pow_w_std = 0; pow_w_max = 0;
% sig_hits_r = 0; type_s_r = 0; type_m_r = 0;
% sig_hits_w = 0; type_s_w = 0; type_m_w = 0;
% mse_r = 0; mse_w = 0;
%
% for s = 1:n_sims
% % 1. Induce Predictor Correlation (r = 0.2)
% X_raw = randn(n_vals, p);
% X = bsxfun(@plus, X_raw * 0.8944, randn(n_vals, 1) * 0.4472);
% X = [ones(n_vals, 1), X];
%
% % 2. Setup Signal (Variable 2 is the only true signal)
% beta_true = zeros(p+1, q);
% beta_true(2, :) = snr;
%
% % 3. Induce Outcome Noise Correlation (r = 0.2)
% noise_unique = randn(n_vals, q);
% noise_common = randn(n_vals, 1);
% E = bsxfun(@plus, noise_unique * 0.8944, noise_common * 0.4472);
%
% % 4. Generate Y
% y_raw = X * beta_true + E;
% y = (y_raw - mean(y_raw)) ./ std(y_raw);
%
% S_r = bootridge(y, X, [], 200, alpha, [], 1, s);
%
% rej_w_std = false(p+1, q);
% rej_w_max = false(p+1, q);
% coeffs_w = zeros(p+1, q);
% for j = 1:q
% res_std = bootwild(y(:,j), X, [], 1999, alpha, s, 0);
% res_max = bootwild(y(:,j), X, [], 1999, {alpha}, s, 1);
% rej_w_std(:, j) = (res_std.pval <= alpha);
% rej_w_max(:, j) = (res_max.pval <= alpha);
% coeffs_w(:, j) = res_max.original;
% end
%
% % --- Indices ---
% null_idx = 3:(p+1);
% sig_idx = 2;
%
% % --- Ridge Decisions ---
% dec_r_ci = (S_r.CI_lower > 0 | S_r.CI_upper < 0);
% dec_r_bf = (S_r.lnBF10 >= 1);
% dec_r_ss = (S_r.stability > (1 - alpha/2));
%
% % --- FDR Calculation ---
% fd = sum(sum(dec_r_ci(null_idx, :)));
% td = sum(sum(dec_r_ci(2:(p+1), :)));
% if td > 0, fdr_r_ci = fdr_r_ci + (fd/td); end
%
% fd = sum(sum(dec_r_bf(null_idx, :)));
% td = sum(sum(dec_r_bf(2:(p+1), :)));
% if td > 0, fdr_r_bf = fdr_r_bf + (fd/td); end
%
% fd = sum(sum(dec_r_ss(null_idx, :)));
% td = sum(sum(dec_r_ss(2:(p+1), :)));
% if td > 0, fdr_r_ss = fdr_r_ss + (fd/td); end
%
% fd = sum(sum(rej_w_std(null_idx, :)));
% td = sum(sum(rej_w_std(2:(p+1), :)));
% if td > 0, fdr_w_std = fdr_w_std + (fd/td); end
%
% fd = sum(sum(rej_w_max(null_idx, :)));
% td = sum(sum(rej_w_max(2:(p+1), :)));
% if td > 0, fdr_w_max = fdr_w_max + (fd/td); end
%
% % --- FPR ---
% num_null_total = length(null_idx) * q;
% fpr_r_ci = fpr_r_ci + (sum(sum(dec_r_ci(null_idx, :))) / ...
% num_null_total);
% fpr_r_bf = fpr_r_bf + (sum(sum(dec_r_bf(null_idx, :))) / ...
% num_null_total);
% fpr_r_ss = fpr_r_ss + (sum(sum(dec_r_ss(null_idx, :))) / ...
% num_null_total);
% fpr_w_std = fpr_w_std + (sum(sum(rej_w_std(null_idx, :))) / ...
% num_null_total);
% fpr_w_max = fpr_w_max + (sum(sum(rej_w_max(null_idx, :))) / ...
% num_null_total);
%
% % --- Signal Analysis ---
% pow_r_ci = pow_r_ci + (sum(dec_r_ci(sig_idx, :)) / q);
% pow_r_bf = pow_r_bf + (sum(dec_r_bf(sig_idx, :)) / q);
% pow_r_ss = pow_r_ss + (sum(dec_r_ss(sig_idx, :)) / q);
% pow_w_std = pow_w_std + (sum(rej_w_std(sig_idx, :)) / q);
% pow_w_max = pow_w_max + (sum(rej_w_max(sig_idx, :)) / q);
%
% for j = 1:q
% if dec_r_ci(sig_idx, j)
% sig_hits_r = sig_hits_r + 1;
% if sign(S_r.coefficient(2,j)) ~= sign(snr)
% type_s_r = type_s_r + 1;
% end
% type_m_r = type_m_r + (abs(S_r.coefficient(2,j)) / abs(snr));
% end
% if rej_w_max(sig_idx, j)
% sig_hits_w = sig_hits_w + 1;
% if sign(coeffs_w(2,j)) ~= sign(snr)
% type_s_w = type_s_w + 1;
% end
% type_m_w = type_m_w + (abs(coeffs_w(2,j)) / abs(snr));
% end
% end
%
% X_test = [ones(50, 1), randn(50, p)];
% y_test_raw = X_test * beta_true + randn(50, q);
% y_test = (y_test_raw - mean(y_test_raw)) ./ std(y_test_raw);
% mse_r = mse_r + mean(mean((y_test - X_test*S_r.coefficient).^2));
% mse_w = mse_w + mean(mean((y_test - X_test*coeffs_w).^2));
% end
%
% end
% end
% end
%
% | |--- MSE ---|
% Cond (p,q) | SNR |Ridge Wild
% ------------------------------|
% p3 q1 | 0.1 |1.00 1.07 |
% p3 q1 | 0.2 |0.98 1.04 |
% p3 q1 | 0.4 |0.90 0.91 |
% p3 q1 | 0.8 |0.68 0.69 |
% ------------------------------|
% p3 q5 | 0.1 |0.99 1.06 |
% p3 q5 | 0.2 |0.97 1.03 |
% p3 q5 | 0.4 |0.90 0.94 |
% p3 q5 | 0.8 |0.68 0.70 |
% ------------------------------|
% p3 q10 | 0.1 |0.99 1.07 |
% p3 q10 | 0.2 |0.97 1.03 |
% p3 q10 | 0.4 |0.90 0.94 |
% p3 q10 | 0.8 |0.66 0.67 |
% ------------------------------|
% p10 q1 | 0.1 |1.01 1.38 |
% p10 q1 | 0.2 |1.02 1.39 |
% p10 q1 | 0.4 |0.98 1.24 |
% p10 q1 | 0.8 |0.77 0.85 |
% ------------------------------|
% p10 q5 | 0.1 |1.00 1.37 |
% p10 q5 | 0.2 |0.99 1.35 |
% p10 q5 | 0.4 |0.94 1.21 |
% p10 q5 | 0.8 |0.75 0.88 |
% ------------------------------|
% p10 q10 | 0.1 |1.00 1.42 |
% p10 q10 | 0.2 |0.99 1.36 |
% p10 q10 | 0.4 |0.95 1.25 |
% p10 q10 | 0.8 |0.74 0.87 |
% ------------------------------|
% p30 q1 | 0.1 |1.13 5.49 |
% p30 q1 | 0.2 |1.07 5.02 |
% p30 q1 | 0.4 |1.05 4.51 |
% p30 q1 | 0.8 |0.94 3.20 |
% ------------------------------|
% p30 q5 | 0.1 |1.07 5.36 |
% p30 q5 | 0.2 |1.04 5.34 |
% p30 q5 | 0.4 |1.04 4.39 |
% p30 q5 | 0.8 |0.90 3.58 |
% ------------------------------|
% p30 q10 | 0.1 |1.04 5.95 |
% p30 q10 | 0.2 |1.05 5.71 |
% p30 q10 | 0.4 |1.02 4.86 |
% p30 q10 | 0.8 |0.87 3.18 |
% ------------------------------|
% | |--- Ridge Pow --- | Wild Pow |
% Cond (p,q) | SNR |CI BF SS | Std MaxT |
% ---------------------------------------------------|
% p3 q1 | 0.1 |0.10 0.13 0.17 | 0.13 0.07 |
% p3 q1 | 0.2 |0.07 0.10 0.20 | 0.20 0.10 |
% p3 q1 | 0.4 |0.30 0.40 0.60 | 0.47 0.23 |
% p3 q1 | 0.8 |0.97 1.00 1.00 | 1.00 0.90 |
% ---------------------------------------------------|
% p3 q5 | 0.1 |0.00 0.01 0.09 | 0.09 0.01 |
% p3 q5 | 0.2 |0.10 0.15 0.32 | 0.23 0.12 |
% p3 q5 | 0.4 |0.39 0.57 0.70 | 0.61 0.35 |
% p3 q5 | 0.8 |1.00 1.00 1.00 | 0.99 0.97 |
% ---------------------------------------------------|
% p3 q10 | 0.1 |0.02 0.07 0.12 | 0.10 0.05 |
% p3 q10 | 0.2 |0.08 0.15 0.29 | 0.23 0.10 |
% p3 q10 | 0.4 |0.50 0.62 0.68 | 0.64 0.49 |
% p3 q10 | 0.8 |0.95 0.97 0.97 | 0.95 0.89 |
% ---------------------------------------------------|
% p10 q1 | 0.1 |0.03 0.07 0.20 | 0.13 0.00 |
% p10 q1 | 0.2 |0.03 0.03 0.17 | 0.07 0.03 |
% p10 q1 | 0.4 |0.23 0.43 0.53 | 0.43 0.13 |
% p10 q1 | 0.8 |0.90 0.97 1.00 | 0.97 0.83 |
% ---------------------------------------------------|
% p10 q5 | 0.1 |0.02 0.05 0.14 | 0.10 0.01 |
% p10 q5 | 0.2 |0.02 0.07 0.28 | 0.19 0.05 |
% p10 q5 | 0.4 |0.29 0.50 0.65 | 0.47 0.23 |
% p10 q5 | 0.8 |0.94 0.97 0.99 | 0.97 0.82 |
% ---------------------------------------------------|
% p10 q10 | 0.1 |0.00 0.00 0.09 | 0.07 0.00 |
% p10 q10 | 0.2 |0.01 0.06 0.24 | 0.15 0.02 |
% p10 q10 | 0.4 |0.29 0.46 0.71 | 0.51 0.23 |
% p10 q10 | 0.8 |0.94 0.98 0.99 | 0.96 0.79 |
% ---------------------------------------------------|
% p30 q1 | 0.1 |0.00 0.00 0.10 | 0.00 0.00 |
% p30 q1 | 0.2 |0.00 0.03 0.17 | 0.13 0.03 |
% p30 q1 | 0.4 |0.17 0.30 0.67 | 0.17 0.03 |
% p30 q1 | 0.8 |0.83 0.90 1.00 | 0.57 0.10 |
% ---------------------------------------------------|
% p30 q5 | 0.1 |0.01 0.02 0.15 | 0.11 0.02 |
% p30 q5 | 0.2 |0.00 0.01 0.23 | 0.09 0.01 |
% p30 q5 | 0.4 |0.13 0.33 0.71 | 0.25 0.07 |
% p30 q5 | 0.8 |0.71 0.87 0.98 | 0.45 0.17 |
% ---------------------------------------------------|
% p30 q10 | 0.1 |0.00 0.00 0.15 | 0.11 0.01 |
% p30 q10 | 0.2 |0.01 0.06 0.27 | 0.11 0.01 |
% p30 q10 | 0.4 |0.05 0.22 0.57 | 0.17 0.02 |
% p30 q10 | 0.8 |0.74 0.89 0.97 | 0.54 0.15 |
% ---------------------------------------------------|
% | |Ridge Errors | Wild Errors |
% Cond (p,q) | SNR |TypeS TypeM | TypeS TypeM |
% -------------------------------------------------|
% p3 q1 | 0.1 |0.333 3.53 | 0.500 4.89 |
% p3 q1 | 0.2 |0.000 2.02 | 0.000 2.47 |
% p3 q1 | 0.4 |0.000 0.86 | 0.000 1.17 |
% p3 q1 | 0.8 |0.000 0.66 | 0.000 0.79 |
% -------------------------------------------------|
% p3 q5 | 0.1 |0.000 ND | 0.000 3.42 |
% p3 q5 | 0.2 |0.000 1.29 | 0.000 2.15 |
% p3 q5 | 0.4 |0.000 0.80 | 0.000 1.23 |
% p3 q5 | 0.8 |0.000 0.70 | 0.000 0.81 |
% -------------------------------------------------|
% p3 q10 | 0.1 |0.000 2.55 | 0.067 4.27 |
% p3 q10 | 0.2 |0.000 1.33 | 0.000 2.46 |
% p3 q10 | 0.4 |0.000 0.82 | 0.000 1.19 |
% p3 q10 | 0.8 |0.000 0.67 | 0.000 0.81 |
% -------------------------------------------------|
% p10 q1 | 0.1 |0.000 1.90 | 0.000 0.00 |
% p10 q1 | 0.2 |0.000 1.49 | 0.000 2.51 |
% p10 q1 | 0.4 |0.000 0.84 | 0.000 1.47 |
% p10 q1 | 0.8 |0.000 0.54 | 0.000 0.82 |
% -------------------------------------------------|
% p10 q5 | 0.1 |0.000 2.36 | 0.000 6.21 |
% p10 q5 | 0.2 |0.000 1.10 | 0.000 2.83 |
% p10 q5 | 0.4 |0.000 0.65 | 0.000 1.38 |
% p10 q5 | 0.8 |0.000 0.57 | 0.000 0.86 |
% -------------------------------------------------|
% p10 q10 | 0.1 |0.000 ND | 0.000 ND |
% p10 q10 | 0.2 |0.000 1.05 | 0.000 2.54 |
% p10 q10 | 0.4 |0.000 0.69 | 0.000 1.47 |
% p10 q10 | 0.8 |0.000 0.52 | 0.000 0.84 |
% -------------------------------------------------|
% p30 q1 | 0.1 |0.000 ND | 0.000 ND |
% p30 q1 | 0.2 |0.000 ND | 0.000 4.21 |
% p30 q1 | 0.4 |0.000 0.74 | 0.000 3.27 |
% p30 q1 | 0.8 |0.000 0.39 | 0.000 1.38 |
% -------------------------------------------------|
% p30 q5 | 0.1 |0.000 3.28 | 0.000 10.07 |
% p30 q5 | 0.2 |0.000 ND | 0.000 3.71 |
% p30 q5 | 0.4 |0.000 0.59 | 0.000 1.88 |
% p30 q5 | 0.8 |0.000 0.37 | 0.000 1.09 |
% -------------------------------------------------|
% p30 q10 | 0.1 |0.000 ND | 0.000 8.19 |
% p30 q10 | 0.2 |0.000 1.16 | 0.000 5.66 |
% p30 q10 | 0.4 |0.000 0.58 | 0.000 2.61 |
% p30 q10 | 0.8 |0.000 0.39 | 0.000 1.05 |
% -------------------------------------------------|
% | |--- Ridge FPR --- | Wild FPR |
% Cond (p,q) | SNR |CI BF SS | Std MaxT |
% ---------------------------------------------------|
% p3 q1 | 0.1 |0.000 0.000 0.000 | 0.017 0.000 |
% p3 q1 | 0.2 |0.000 0.033 0.050 | 0.017 0.000 |
% p3 q1 | 0.4 |0.017 0.017 0.033 | 0.067 0.017 |
% p3 q1 | 0.8 |0.033 0.050 0.083 | 0.050 0.017 |
% ---------------------------------------------------|
% p3 q5 | 0.1 |0.003 0.023 0.077 | 0.050 0.027 |
% p3 q5 | 0.2 |0.010 0.030 0.093 | 0.067 0.017 |
% p3 q5 | 0.4 |0.040 0.060 0.093 | 0.080 0.027 |
% p3 q5 | 0.8 |0.023 0.023 0.040 | 0.050 0.003 |
% ---------------------------------------------------|
% p3 q10 | 0.1 |0.008 0.025 0.075 | 0.073 0.023 |
% p3 q10 | 0.2 |0.002 0.015 0.052 | 0.047 0.007 |
% p3 q10 | 0.4 |0.025 0.048 0.088 | 0.078 0.037 |
% p3 q10 | 0.8 |0.048 0.050 0.077 | 0.067 0.038 |
% ---------------------------------------------------|
% p10 q1 | 0.1 |0.004 0.019 0.085 | 0.059 0.004 |
% p10 q1 | 0.2 |0.011 0.019 0.074 | 0.067 0.004 |
% p10 q1 | 0.4 |0.019 0.033 0.085 | 0.063 0.015 |
% p10 q1 | 0.8 |0.022 0.037 0.052 | 0.063 0.007 |
% ---------------------------------------------------|
% p10 q5 | 0.1 |0.000 0.004 0.065 | 0.066 0.005 |
% p10 q5 | 0.2 |0.001 0.009 0.070 | 0.071 0.004 |
% p10 q5 | 0.4 |0.004 0.016 0.073 | 0.058 0.010 |
% p10 q5 | 0.8 |0.024 0.046 0.073 | 0.075 0.010 |
% ---------------------------------------------------|
% p10 q10 | 0.1 |0.000 0.005 0.065 | 0.066 0.007 |
% p10 q10 | 0.2 |0.001 0.009 0.068 | 0.059 0.008 |
% p10 q10 | 0.4 |0.006 0.024 0.073 | 0.067 0.009 |
% p10 q10 | 0.8 |0.016 0.037 0.071 | 0.072 0.008 |
% ---------------------------------------------------|
% p30 q1 | 0.1 |0.002 0.017 0.084 | 0.070 0.007 |
% p30 q1 | 0.2 |0.009 0.014 0.083 | 0.074 0.009 |
% p30 q1 | 0.4 |0.001 0.013 0.079 | 0.052 0.001 |
% p30 q1 | 0.8 |0.009 0.021 0.078 | 0.069 0.008 |
% ---------------------------------------------------|
% p30 q5 | 0.1 |0.002 0.008 0.090 | 0.088 0.006 |
% p30 q5 | 0.2 |0.001 0.006 0.077 | 0.077 0.008 |
% p30 q5 | 0.4 |0.003 0.015 0.089 | 0.076 0.003 |
% p30 q5 | 0.8 |0.005 0.024 0.094 | 0.094 0.010 |
% ---------------------------------------------------|
% p30 q10 | 0.1 |0.001 0.005 0.077 | 0.086 0.007 |
% p30 q10 | 0.2 |0.001 0.005 0.084 | 0.089 0.010 |
% p30 q10 | 0.4 |0.000 0.010 0.083 | 0.081 0.004 |
% p30 q10 | 0.8 |0.005 0.024 0.089 | 0.084 0.006 |
% ---------------------------------------------------|
% | |------ Ridge FDR ------ | Wild FDR |
% Cond (p,q) | SNR |FD-CI FD-BF FD-SS | Std MaxT |
% ---------------------------------------------------------|
% p3 q1 | 0.1 |0.000 0.000 0.000 | 0.033 0.000 |
% p3 q1 | 0.2 |0.000 0.067 0.083 | 0.033 0.000 |
% p3 q1 | 0.4 |0.017 0.017 0.050 | 0.083 0.017 |
% p3 q1 | 0.8 |0.033 0.050 0.083 | 0.050 0.017 |
% ---------------------------------------------------------|
% p3 q5 | 0.1 |0.033 0.183 0.450 | 0.356 0.217 |
% p3 q5 | 0.2 |0.083 0.178 0.367 | 0.367 0.119 |
% p3 q5 | 0.4 |0.116 0.145 0.178 | 0.173 0.086 |
% p3 q5 | 0.8 |0.036 0.034 0.060 | 0.074 0.007 |
% ---------------------------------------------------------|
% p3 q10 | 0.1 |0.140 0.241 0.551 | 0.501 0.271 |
% p3 q10 | 0.2 |0.008 0.117 0.304 | 0.282 0.069 |
% p3 q10 | 0.4 |0.088 0.130 0.194 | 0.188 0.122 |
% p3 q10 | 0.8 |0.081 0.083 0.127 | 0.111 0.076 |
% ---------------------------------------------------------|
% p10 q1 | 0.1 |0.033 0.133 0.456 | 0.383 0.033 |
% p10 q1 | 0.2 |0.100 0.150 0.522 | 0.422 0.033 |
% p10 q1 | 0.4 |0.106 0.206 0.461 | 0.372 0.100 |
% p10 q1 | 0.8 |0.089 0.156 0.211 | 0.256 0.033 |
% ---------------------------------------------------------|
% p10 q5 | 0.1 |0.000 0.092 0.788 | 0.848 0.200 |
% p10 q5 | 0.2 |0.050 0.200 0.709 | 0.771 0.122 |
% p10 q5 | 0.4 |0.064 0.147 0.498 | 0.501 0.175 |
% p10 q5 | 0.8 |0.137 0.242 0.345 | 0.374 0.073 |
% ---------------------------------------------------------|
% p10 q10 | 0.1 |0.033 0.300 0.848 | 0.903 0.433 |
% p10 q10 | 0.2 |0.100 0.360 0.720 | 0.753 0.397 |
% p10 q10 | 0.4 |0.115 0.279 0.483 | 0.558 0.243 |
% p10 q10 | 0.8 |0.114 0.233 0.372 | 0.380 0.076 |
% ---------------------------------------------------------|
% p30 q1 | 0.1 |0.067 0.300 0.910 | 0.567 0.100 |
% p30 q1 | 0.2 |0.133 0.233 0.867 | 0.580 0.156 |
% p30 q1 | 0.4 |0.033 0.192 0.661 | 0.494 0.017 |
% p30 q1 | 0.8 |0.111 0.213 0.644 | 0.564 0.128 |
% ---------------------------------------------------------|
% p30 q5 | 0.1 |0.158 0.420 0.950 | 0.967 0.353 |
% p30 q5 | 0.2 |0.133 0.400 0.905 | 0.970 0.292 |
% p30 q5 | 0.4 |0.188 0.483 0.772 | 0.903 0.217 |
% p30 q5 | 0.8 |0.130 0.384 0.722 | 0.775 0.325 |
% ---------------------------------------------------------|
% p30 q10 | 0.1 |0.167 0.500 0.936 | 0.954 0.458 |
% p30 q10 | 0.2 |0.092 0.593 0.898 | 0.957 0.652 |
% p30 q10 | 0.4 |0.058 0.490 0.804 | 0.931 0.500 |
% p30 q10 | 0.8 |0.168 0.398 0.717 | 0.810 0.490 |
% ---------------------------------------------------------|
gives an example of how 'bootridge' is used.
Package: statistics-resampling