Categories &

Functions List

Function Reference: regress_gp

statistics: [Yfit, Yint, m, K] = regress_gp (X, Y, Xfit)
statistics: [Yfit, Yint, m, K] = regress_gp (X, Y, Xfit, "linear")
statistics: [Yfit, Yint, Ysd] = regress_gp (X, Y, Xfit, "rbf")
statistics: […] = regress_gp (X, Y, Xfit, "linear", Sp)
statistics: […] = regress_gp (X, Y, Xfit, Sp)
statistics: […] = regress_gp (X, Y, Xfit, "rbf", theta)
statistics: […] = regress_gp (X, Y, Xfit, "rbf", theta, g)
statistics: […] = regress_gp (X, Y, Xfit, "rbf", theta, g, alpha)
statistics: […] = regress_gp (X, Y, Xfit, theta)
statistics: […] = regress_gp (X, Y, Xfit, theta, g)
statistics: […] = regress_gp (X, Y, Xfit, theta, g, alpha)

Regression using Gaussian Processes.

[Yfit, Yint, m, K] = regress_gp (X, Y, Xfit) will estimate a linear Gaussian Process model m in the form Y = X' * m, where X is an N×P matrix with N observations in P dimensional space and Y is an N×1 column vector as the dependent variable. The information about errors of the predictions (interpolation/extrapolation) is given by the covarianve matrix K. By default, the linear model defines the prior covariance of m as Sp = 100 * eye (size (X, 2) + 1). A custom prior covariance matrix can be passed as Sp, which must be a P+1×P+1 positive definite matrix. The model is evaluated for input Xfit, which must have the same columns as X, and the estimates are returned in Yfit along with the estimated variation in Yint. Yint(:,1) contains the upper boundary estimate and Yint(:,1) contains the upper boundary estimate with respect to Yfit.

[Yfit, Yint, Ysd, K] = regress_gp (X, Y, Xfit, "rbf") will estimate a Gaussian Process model with a Radial Basis Function (RBF) kernel with default parameters theta = 5, which corresponds to the characteristic lengthscale, and g = 0.01, which corresponds to the nugget effect, and alpha = 0.05 which defines the confidence level for the estimated intervals returned in Yint. The function also returns the predictive covariance matrix in Ysd. For multidimensional predictors X the function will automatically normalize each column to a zero mean and a standard deviation to one.

Run demo regress_gp to see examples.

See also: regress, regression_ftest, regression_ttest

Source Code: regress_gp

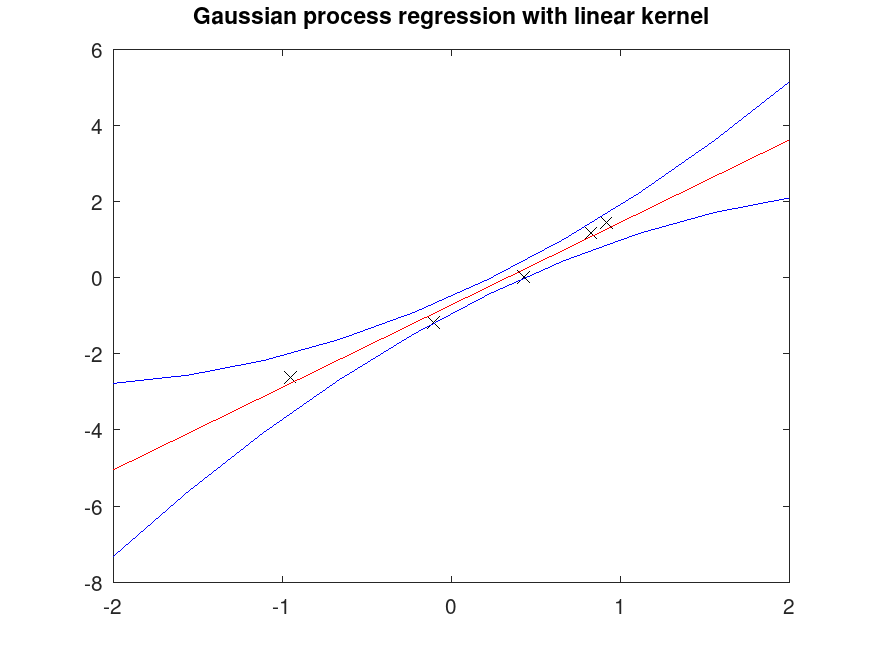
Example: 1

  

 ## Linear fitting of 1D Data
 rand ("seed", 125);
 X = 2 * rand (5, 1) - 1;
 randn ("seed", 25);
 Y = 2 * X - 1 + 0.3 * randn (5, 1);

 ## Points for interpolation/extrapolation
 Xfit = linspace (-2, 2, 10)';

 ## Fit regression model
 [Yfit, Yint, m] = regress_gp (X, Y, Xfit);

 ## Plot fitted data
 plot (X, Y, "xk", Xfit, Yfit, "r-", Xfit, Yint, "b-");
 title ("Gaussian process regression with linear kernel");
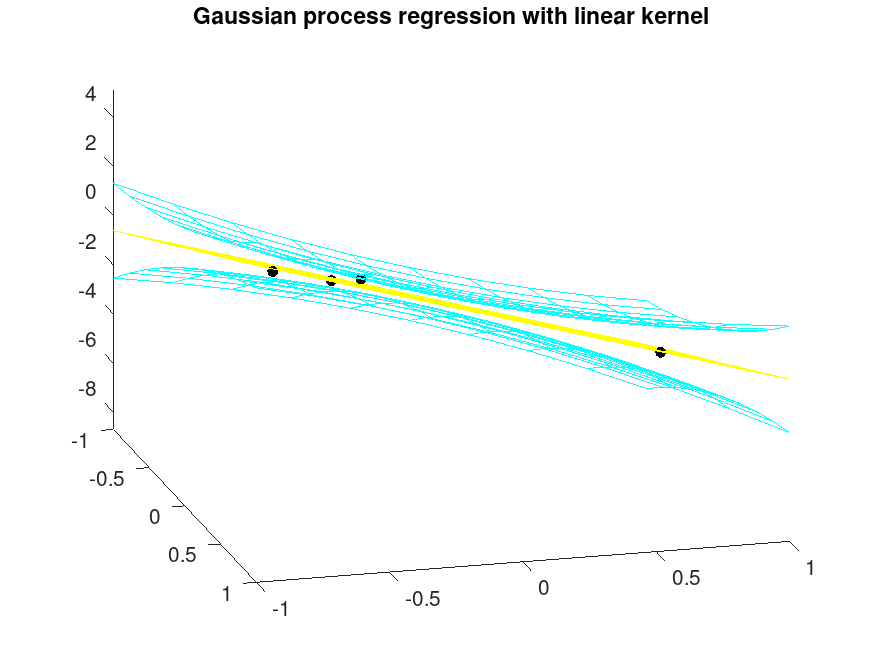
plotted figure

Example: 2

  

 ## Linear fitting of 2D Data
 rand ("seed", 135);
 X = 2 * rand (4, 2) - 1;
 randn ("seed", 35);
 Y = 2 * X(:,1) - 3 * X(:,2) - 1 + 1 * randn (4, 1);

 ## Mesh for interpolation/extrapolation
 [x1, x2] = meshgrid (linspace (-1, 1, 10));
 Xfit = [x1(:), x2(:)];

 ## Fit regression model
 [Ypred, Yint, Ysd] = regress_gp (X, Y, Xfit);
 Ypred = reshape (Ypred, 10, 10);
 YintU = reshape (Yint(:,1), 10, 10);
 YintL = reshape (Yint(:,2), 10, 10);

 ## Plot fitted data
 plot3 (X(:,1), X(:,2), Y, ".k", "markersize", 16);
 hold on;
 h = mesh (x1, x2, Ypred, zeros (10, 10));
 set (h, "facecolor", "none", "edgecolor", "yellow");
 h = mesh (x1, x2, YintU, ones (10, 10));
 set (h, "facecolor", "none", "edgecolor", "cyan");
 h = mesh (x1, x2, YintL, ones (10, 10));
 set (h, "facecolor", "none", "edgecolor", "cyan");
 hold off
 axis tight
 view (75, 25)
 title ("Gaussian process regression with linear kernel");
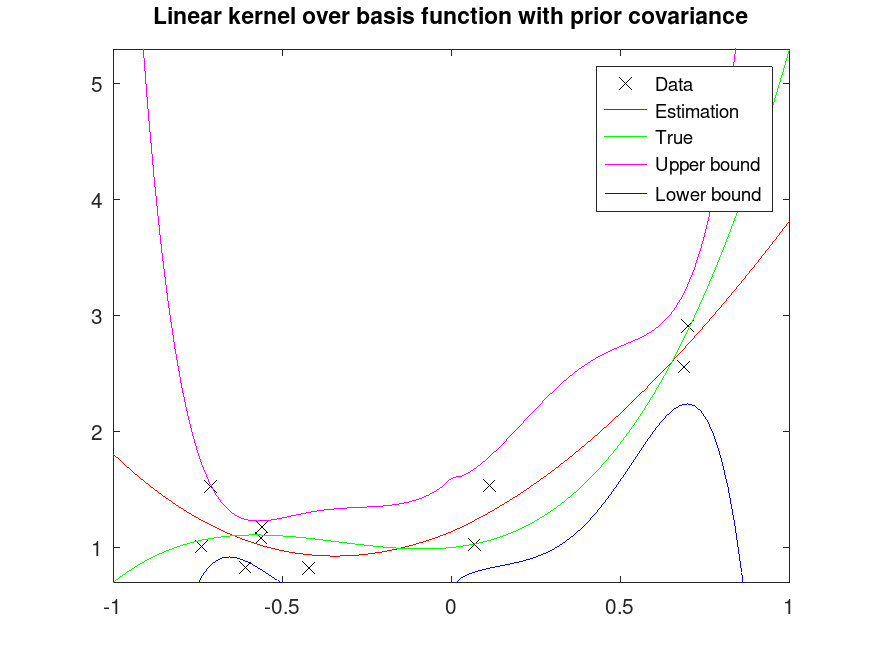
plotted figure

Example: 3

  

 ## Projection over basis function with linear kernel
 pp = [2, 2, 0.3, 1];
 n = 10;
 rand ("seed", 145);
 X = 2 * rand (n, 1) - 1;
 randn ("seed", 45);
 Y = polyval (pp, X) + 0.3 * randn (n, 1);

 ## Powers
 px = [sqrt(abs(X)), X, X.^2, X.^3];

 ## Points for interpolation/extrapolation
 Xfit = linspace (-1, 1, 100)';
 pxi = [sqrt(abs(Xfit)), Xfit, Xfit.^2, Xfit.^3];

 ## Define a prior covariance assuming that the sqrt component is not present
 Sp = 100 * eye (size (px, 2) + 1);
 Sp(2,2) = 1; # We don't believe the sqrt(abs(X)) is present

 ## Fit regression model
 [Yfit, Yint, Ysd] = regress_gp (px, Y, pxi, Sp);

 ## Plot fitted data
 plot (X, Y, "xk;Data;", Xfit, Yfit, "r-;Estimation;", ...
                         Xfit, polyval (pp, Xfit), "g-;True;");
 axis tight
 axis manual
 hold on
 plot (Xfit, Yint(:,1), "m-;Upper bound;", Xfit, Yint(:,2), "b-;Lower bound;");
 hold off
 title ("Linear kernel over basis function with prior covariance");
plotted figure

Example: 4

  

 ## Projection over basis function with linear kernel
 pp = [2, 2, 0.3, 1];
 n = 10;
 rand ("seed", 145);
 X = 2 * rand (n, 1) - 1;
 randn ("seed", 45);
 Y = polyval (pp, X) + 0.3 * randn (n, 1);

 ## Powers
 px = [sqrt(abs(X)), X, X.^2, X.^3];

 ## Points for interpolation/extrapolation
 Xfit = linspace (-1, 1, 100)';
 pxi = [sqrt(abs(Xfit)), Xfit, Xfit.^2, Xfit.^3];

 ## Fit regression model without any assumption on prior covariance
 [Yfit, Yint, Ysd] = regress_gp (px, Y, pxi);

 ## Plot fitted data
 plot (X, Y, "xk;Data;", Xfit, Yfit, "r-;Estimation;", ...
                         Xfit, polyval (pp, Xfit), "g-;True;");
 axis tight
 axis manual
 hold on
 plot (Xfit, Yint(:,1), "m-;Upper bound;", Xfit, Yint(:,2), "b-;Lower bound;");
 hold off
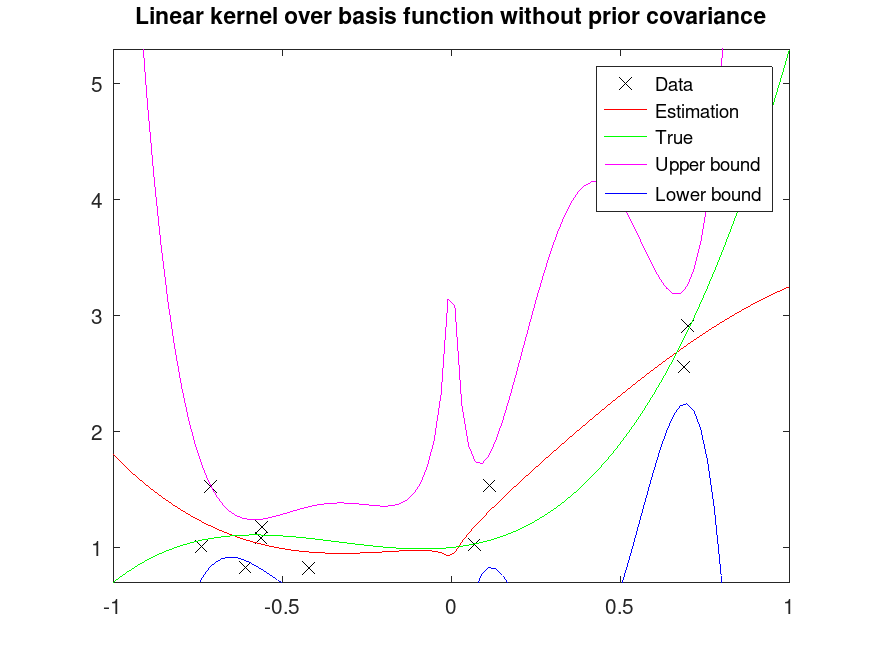
 title ("Linear kernel over basis function without prior covariance");
plotted figure

Example: 5

  

 ## Projection over basis function with rbf kernel
 pp = [2, 2, 0.3, 1];
 n = 10;
 rand ("seed", 145);
 X = 2 * rand (n, 1) - 1;
 randn ("seed", 45);
 Y = polyval (pp, X) + 0.3 * randn (n, 1);

 ## Powers
 px = [sqrt(abs(X)), X, X.^2, X.^3];

 ## Points for interpolation/extrapolation
 Xfit = linspace (-1, 1, 100)';
 pxi = [sqrt(abs(Xfit)), Xfit, Xfit.^2, Xfit.^3];

 ## Fit regression model with RBF kernel (standard parameters)
 [Yfit, Yint, Ysd] = regress_gp (px, Y, pxi, "rbf");

 ## Plot fitted data
 plot (X, Y, "xk;Data;", Xfit, Yfit, "r-;Estimation;", ...
                         Xfit, polyval (pp, Xfit), "g-;True;");
 axis tight
 axis manual
 hold on
 plot (Xfit, Yint(:,1), "m-;Upper bound;", Xfit, Yint(:,2), "b-;Lower bound;");
 hold off
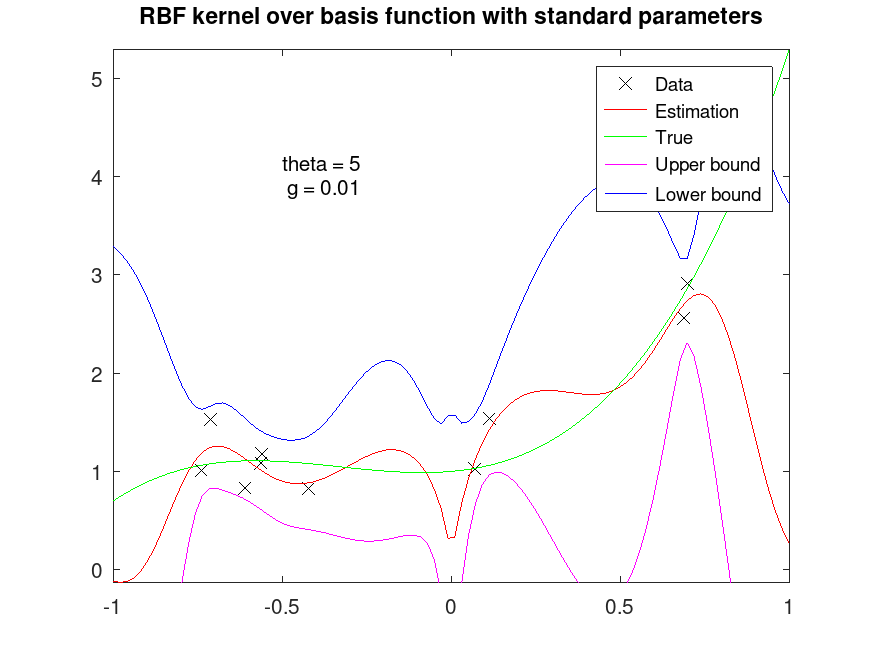
 title ("RBF kernel over basis function with standard parameters");
 text (-0.5, 4, "theta = 5\n g = 0.01");
plotted figure

Example: 6

  

 ## Projection over basis function with rbf kernel
 pp = [2, 2, 0.3, 1];
 n = 10;
 rand ("seed", 145);
 X = 2 * rand (n, 1) - 1;
 randn ("seed", 45);
 Y = polyval (pp, X) + 0.3 * randn (n, 1);

 ## Powers
 px = [sqrt(abs(X)), X, X.^2, X.^3];

 ## Points for interpolation/extrapolation
 Xfit = linspace (-1, 1, 100)';
 pxi = [sqrt(abs(Xfit)), Xfit, Xfit.^2, Xfit.^3];

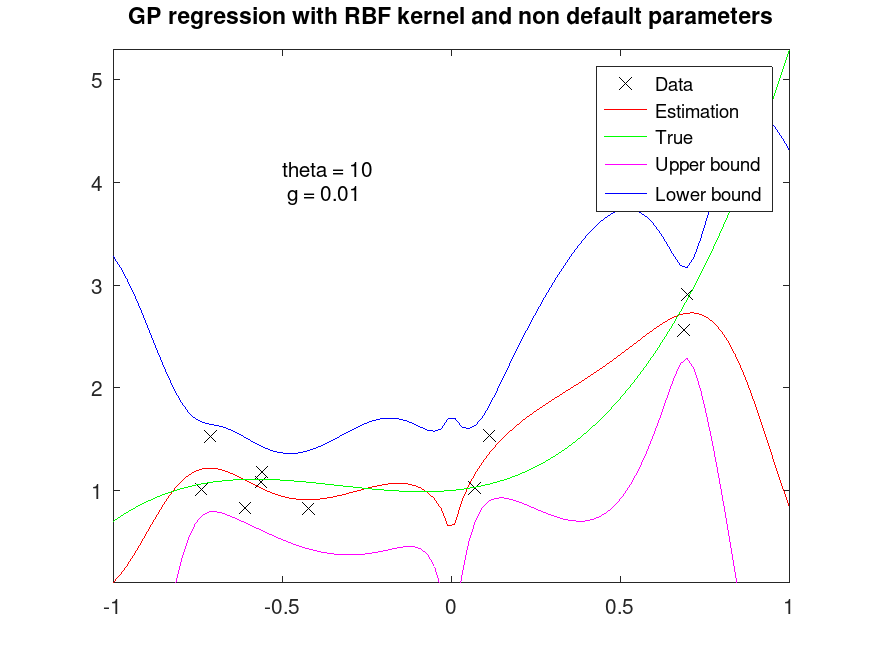
 ## Fit regression model with RBF kernel with different parameters
 [Yfit, Yint, Ysd] = regress_gp (px, Y, pxi, "rbf", 10, 0.01);

 ## Plot fitted data
 plot (X, Y, "xk;Data;", Xfit, Yfit, "r-;Estimation;", ...
                         Xfit, polyval (pp, Xfit), "g-;True;");
 axis tight
 axis manual
 hold on
 plot (Xfit, Yint(:,1), "m-;Upper bound;", Xfit, Yint(:,2), "b-;Lower bound;");
 hold off
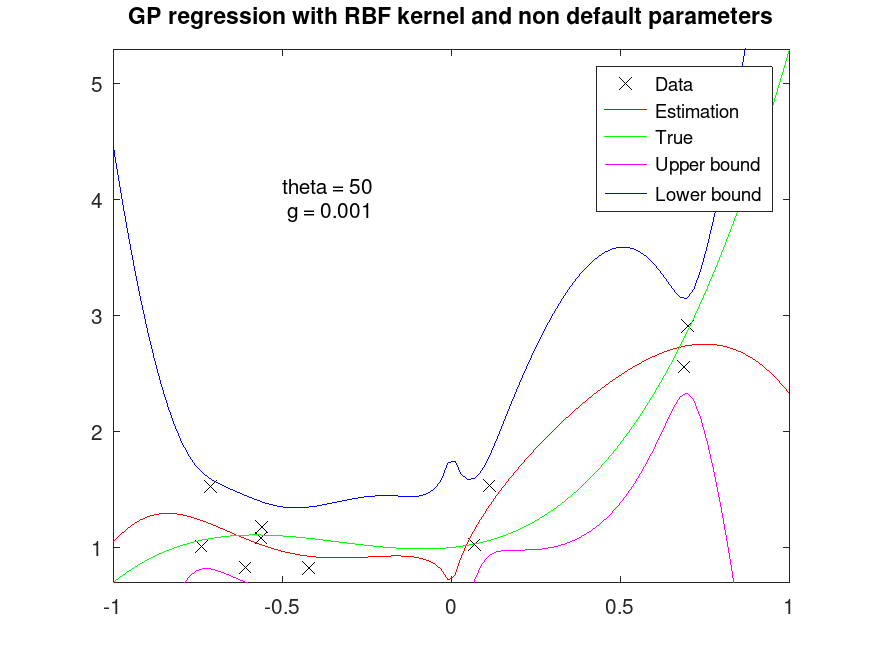
 title ("GP regression with RBF kernel and non default parameters");
 text (-0.5, 4, "theta = 10\n g = 0.01");

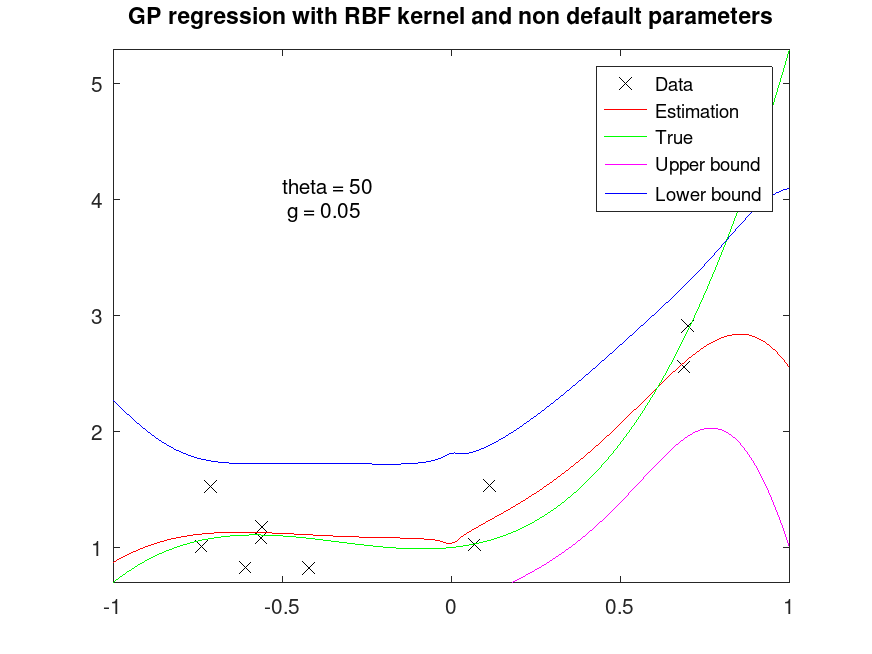
 ## Fit regression model with RBF kernel with different parameters
 [Yfit, Yint, Ysd] = regress_gp (px, Y, pxi, "rbf", 50, 0.01);

 ## Plot fitted data
 figure
 plot (X, Y, "xk;Data;", Xfit, Yfit, "r-;Estimation;", ...
                         Xfit, polyval (pp, Xfit), "g-;True;");
 axis tight
 axis manual
 hold on
 plot (Xfit, Yint(:,1), "m-;Upper bound;", Xfit, Yint(:,2), "b-;Lower bound;");
 hold off
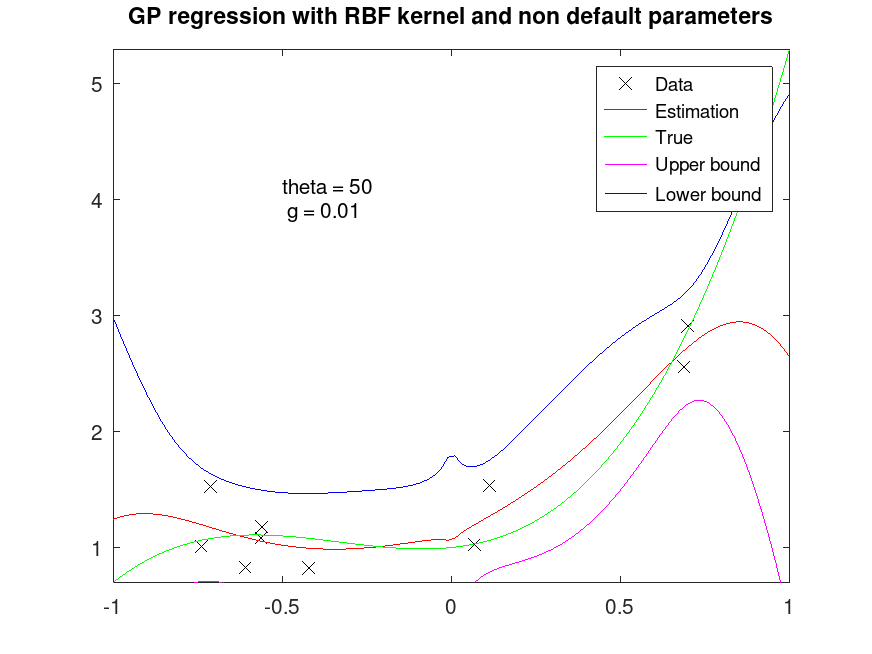
 title ("GP regression with RBF kernel and non default parameters");
 text (-0.5, 4, "theta = 50\n g = 0.01");

 ## Fit regression model with RBF kernel with different parameters
 [Yfit, Yint, Ysd] = regress_gp (px, Y, pxi, "rbf", 50, 0.001);

 ## Plot fitted data
 figure
 plot (X, Y, "xk;Data;", Xfit, Yfit, "r-;Estimation;", ...
                         Xfit, polyval (pp, Xfit), "g-;True;");
 axis tight
 axis manual
 hold on
 plot (Xfit, Yint(:,1), "m-;Upper bound;", Xfit, Yint(:,2), "b-;Lower bound;");
 hold off
 title ("GP regression with RBF kernel and non default parameters");
 text (-0.5, 4, "theta = 50\n g = 0.001");

 ## Fit regression model with RBF kernel with different parameters
 [Yfit, Yint, Ysd] = regress_gp (px, Y, pxi, "rbf", 50, 0.05);

 ## Plot fitted data
 figure
 plot (X, Y, "xk;Data;", Xfit, Yfit, "r-;Estimation;", ...
                         Xfit, polyval (pp, Xfit), "g-;True;");
 axis tight
 axis manual
 hold on
 plot (Xfit, Yint(:,1), "m-;Upper bound;", Xfit, Yint(:,2), "b-;Lower bound;");
 hold off
 title ("GP regression with RBF kernel and non default parameters");
 text (-0.5, 4, "theta = 50\n g = 0.05");
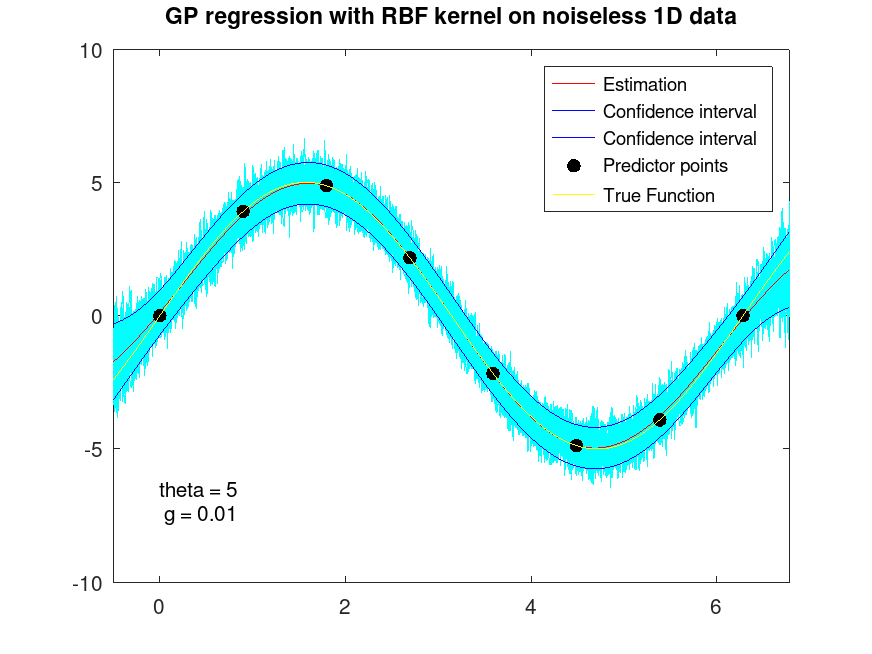
plotted figure

plotted figure

plotted figure

plotted figure

Example: 7

  

 ## RBF fitting on noiseless 1D Data
 x = [0:2*pi/7:2*pi]';
 y = 5 * sin (x);

 ## Predictive grid of 500 equally spaced locations
 xi = [-0.5:(2*pi+1)/499:2*pi+0.5]';

 ## Fit regression model with RBF kernel
 [Yfit, Yint, Ysd] = regress_gp (x, y, xi, "rbf");

 ## Plot fitted data
 r = mvnrnd (Yfit, diag (Ysd)', 50);
 plot (xi, r', "c-");
 hold on
 plot (xi, Yfit, "r-;Estimation;", xi, Yint, "b-;Confidence interval;");
 plot (x, y, ".k;Predictor points;", "markersize", 20)
 plot (xi, 5 * sin (xi), "-y;True Function;");
 xlim ([-0.5,2*pi+0.5]);
 ylim ([-10,10]);
 hold off
 title ("GP regression with RBF kernel on noiseless 1D data");
 text (0, -7, "theta = 5\n g = 0.01");
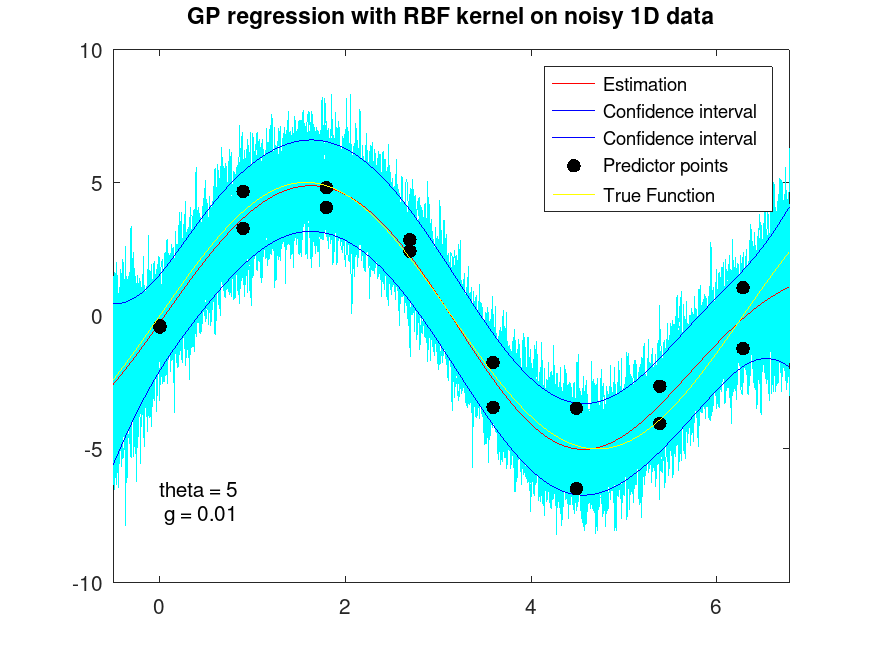
plotted figure

Example: 8

  

 ## RBF fitting on noisy 1D Data
 x = [0:2*pi/7:2*pi]';
 x = [x; x];
 y = 5 * sin (x) + randn (size (x));

 ## Predictive grid of 500 equally spaced locations
 xi = [-0.5:(2*pi+1)/499:2*pi+0.5]';

 ## Fit regression model with RBF kernel
 [Yfit, Yint, Ysd] = regress_gp (x, y, xi, "rbf");

 ## Plot fitted data
 r = mvnrnd (Yfit, diag (Ysd)', 50);
 plot (xi, r', "c-");
 hold on
 plot (xi, Yfit, "r-;Estimation;", xi, Yint, "b-;Confidence interval;");
 plot (x, y, ".k;Predictor points;", "markersize", 20)
 plot (xi, 5 * sin (xi), "-y;True Function;");
 xlim ([-0.5,2*pi+0.5]);
 ylim ([-10,10]);
 hold off
 title ("GP regression with RBF kernel on noisy 1D data");
 text (0, -7, "theta = 5\n g = 0.01");
plotted figure