Statistics: RayleighDistribution

Class Definition: `RayleighDistribution`

statistics: RayleighDistribution

Rayleigh probability distribution object.

A RayleighDistribution object consists of parameters, a model description, and sample data for a Rayleigh probability distribution.

The Rayleigh distribution is a continuous probability distribution for nonnegative random variables. It is often used to model the magnitude of a vector in two dimensions where the components are normally distributed with zero mean and equal variance. It is defined by scale parameter sigma.

There are several ways to create a RayleighDistribution object.

Fit a distribution to data using the fitdist function.
Create a distribution with fixed parameter values using the makedist function.
Use the constructor RayleighDistribution (sigma) to create a Rayleigh distribution with fixed parameter value sigma.
Use the static method RayleighDistribution.fit (x, censor, freq) to fit a distribution to the data in x using the same input arguments as the raylfit function.

It is highly recommended to use fitdist and makedist functions to create probability distribution objects, instead of the class constructor or the aforementioned static method.

Further information about the Rayleigh distribution can be found at https://en.wikipedia.org/wiki/Rayleigh_distribution

See also: fitdist, makedist, raylcdf, raylinv, raylpdf, raylrnd, raylfit, rayllike, raylstat

Source Code: RayleighDistribution

Properties

A positive scalar value characterizing the scale of the Rayleigh distribution. You can access the sigma property using dot name assignment.

Example: 1


 ## Create a Rayleigh distribution object by calling its constructor
 pd = RayleighDistribution (1.5)

 ## Query parameter 'sigma'
 pd.sigma

 ## This demonstrates direct construction with a specific scale parameter,
 ## useful for modeling nonnegative data like signal amplitudes in communications.

pd =
  RayleighDistribution

  Rayleigh distribution
    sigma = 1.5

ans = 1.5000

A character vector specifying the name of the probability distribution object. This property is read-only.

A scalar integer value specifying the number of parameters characterizing the probability distribution. This property is read-only.

A cell array of character vectors with each element containing the name of a distribution parameter. This property is read-only.

A cell array of character vectors with each element containing a short description of a distribution parameter. This property is read-only.

A numeric vector containing the values of the distribution parameters. This property is read-only. You can change the distribution parameters by assigning new values to the sigma property.

A numeric matrix containing the variance-covariance of the parameter estimates. Diagonal elements contain the variance of each estimated parameter, and non-diagonal elements contain the covariance between the parameter estimates. The covariance matrix is only meaningful when the distribution was fitted to data. If the distribution object was created with fixed parameters, or a parameter of a fitted distribution is modified, then all elements of the variance-covariance are zero. This property is read-only.

A logical vector specifying which parameters are fixed and which are estimated. true values correspond to fixed parameters, false values correspond to parameter estimates. This property is read-only.

A $1×2$ numeric vector specifying the truncation interval for the probability distribution. First element contains the lower boundary, second element contains the upper boundary. This property is read-only. You can only truncate a probability distribution with the truncate method.

A logical scalar value specifying whether a probability distribution is truncated or not. This property is read-only.

A scalar structure containing the following fields:

data: a numeric vector containing the data used for distribution fitting.
cens: a numeric vector of logical values indicating censoring information corresponding to the elements of the data used for distribution fitting. If no censoring vector was used for distribution fitting, then this field defaults to an empty array.
freq: a numeric vector of non-negative integer values containing the frequency information corresponding to the elements of the data used for distribution fitting. If no frequency vector was used for distribution fitting, then this field defaults to an empty array.

Methods

RayleighDistribution: p = cdf (pd, x)
RayleighDistribution: p = cdf (pd, x, "upper")

p = cdf (pd, x) computes the CDF of the probability distribution object, pd, evaluated at the values in x.

p = cdf (…, "upper") returns the complement of the CDF of the probability distribution object, pd, evaluated at the values in x.

Example: 1


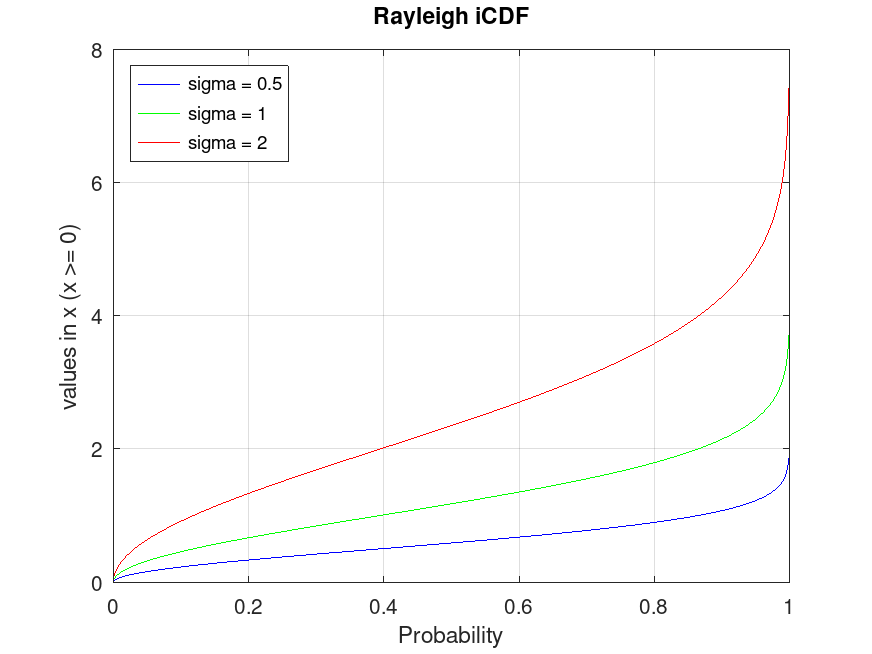
 ## Plot various CDFs from the Rayleigh distribution
 x = -1:0.01:5;
 data1 = raylrnd (0.5, 10000, 1);
 data2 = raylrnd (1.0, 10000, 1);
 data3 = raylrnd (2.0, 10000, 1);
 pd1 = fitdist (data1, "Rayleigh");
 pd2 = fitdist (data2, "Rayleigh");
 pd3 = fitdist (data3, "Rayleigh");
 p1 = cdf (pd1, x);
 p2 = cdf (pd2, x);
 p3 = cdf (pd3, x);
 plot (x, p1, "-b", x, p2, "-g", x, p3, "-r")
 grid on
 legend ({"sigma = 0.5", "sigma = 1", "sigma = 2"}, ...
         "location", "southeast")
 title ("Rayleigh CDF")
 xlabel ("values in x (x >= 0)")
 ylabel ("Cumulative probability")

 ## Use this to compute and visualize the cumulative distribution function
 ## for different Rayleigh distributions, showing how probability
 ## accumulates for nonnegative values, useful in signal processing or physics.

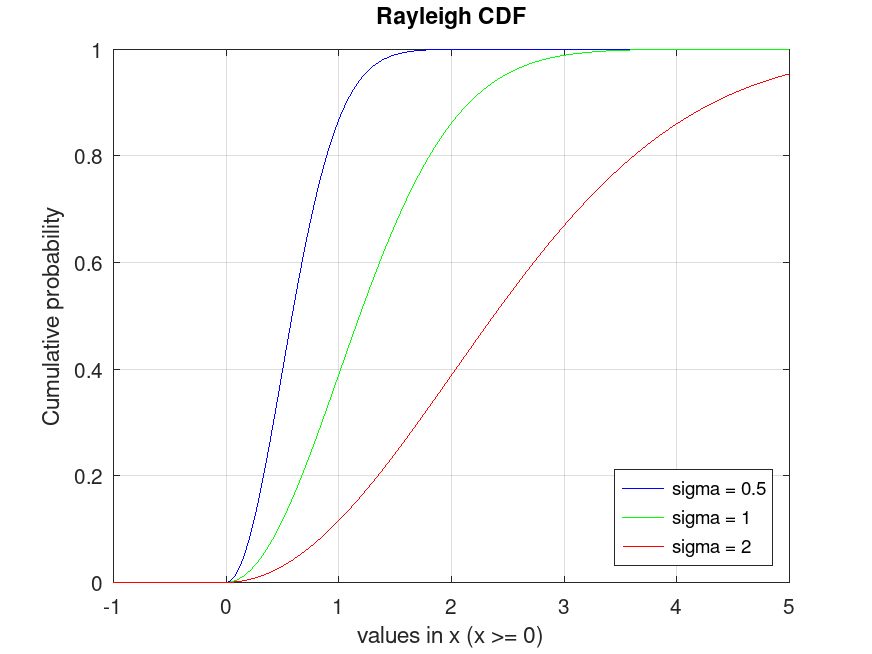
RayleighDistribution: x = icdf (pd, p)

x = icdf (pd, p) computes the quantile (the inverse of the CDF) of the probability distribution object, pd, evaluated at the values in p.

Example: 1


 ## Plot various iCDFs from the Rayleigh distribution
 p = 0.001:0.001:0.999;
 data1 = raylrnd (0.5, 10000, 1);
 data2 = raylrnd (1.0, 10000, 1);
 data3 = raylrnd (2.0, 10000, 1);
 pd1 = fitdist (data1, "Rayleigh");
 pd2 = fitdist (data2, "Rayleigh");
 pd3 = fitdist (data3, "Rayleigh");
 x1 = icdf (pd1, p);
 x2 = icdf (pd2, p);
 x3 = icdf (pd3, p);
 plot (p, x1, "-b", p, x2, "-g", p, x3, "-r")
 grid on
 legend ({"sigma = 0.5", "sigma = 1", "sigma = 2"}, ...
         "location", "northwest")
 title ("Rayleigh iCDF")
 xlabel ("Probability")
 ylabel ("values in x (x >= 0)")

 ## This demonstrates the inverse CDF (quantiles) for Rayleigh
 ## distributions, useful for finding values corresponding to given
 ## probabilities, such as thresholds in radar detection.

RayleighDistribution: r = iqr (pd)

r = iqr (pd) computes the interquartile range of the probability distribution object, pd.

Example: 1


 ## Compute the interquartile range for a Rayleigh distribution
 data = raylrnd (1, 10000, 1);
 pd = fitdist (data, "Rayleigh");
 iqr_value = iqr (pd)

 ## Use this to calculate the interquartile range, which measures the spread
 ## of the middle 50% of the distribution, helpful for understanding central
 ## variability in nonnegative data.

iqr_value = 0.9024

RayleighDistribution: m = mean (pd)

m = mean (pd) computes the mean of the probability distribution object, pd.

Example: 1


 ## Compute the mean for different Rayleigh distributions
 data1 = raylrnd (0.5, 10000, 1);
 data2 = raylrnd (1.0, 10000, 1);
 pd1 = fitdist (data1, "Rayleigh");
 pd2 = fitdist (data2, "Rayleigh");
 mean1 = mean (pd1)
 mean2 = mean (pd2)

 ## This shows how to compute the expected value for Rayleigh
 ## distributions with different scale parameters, representing average
 ## magnitude in applications like acoustics.

mean1 = 0.6212
mean2 = 1.2431

RayleighDistribution: m = median (pd)

m = median (pd) computes the median of the probability distribution object, pd.

Example: 1


 ## Compute the median for different Rayleigh distributions
 data1 = raylrnd (0.5, 10000, 1);
 data2 = raylrnd (1.0, 10000, 1);
 pd1 = fitdist (data1, "Rayleigh");
 pd2 = fitdist (data2, "Rayleigh");
 median1 = median (pd1)
 median2 = median (pd2)

 ## Use this to find the median value, which splits the distribution
 ## into two equal probability halves, robust to skewness in nonnegative data.

median1 = 0.5892
median2 = 1.1769

RayleighDistribution: nlogL = negloglik (pd)

nlogL = negloglik (pd) computes the negative loglikelihood of the probability distribution object, pd.

Example: 1


 ## Compute the negative loglikelihood for a fitted Rayleigh distribution
 rand ("seed", 21);
 data = raylrnd (1, 100, 1);
 pd_fitted = fitdist (data, "Rayleigh");
 nlogL = negloglik (pd_fitted)

 ## This is useful for assessing the fit of a Rayleigh distribution to
 ## data, with lower values indicating a better fit, often used in model comparison.

nlogL = -91.102

RayleighDistribution: ci = paramci (pd)
RayleighDistribution: ci = paramci (pd, Name, Value)

ci = paramci (pd) computes the lower and upper boundaries of the 95% confidence interval for each parameter of the probability distribution object, pd.

ci = paramci (pd, Name, Value) computes the confidence intervals with additional options specified by Name-Value pair arguments listed below.

`Name`		`Value`
`"Alpha"`		A scalar value in the range $(0,1)$ specifying the significance level for the confidence interval. The default value 0.05 corresponds to a 95% confidence interval.
`"Parameter"`		A character vector or a cell array of character vectors specifying the parameter names for which to compute confidence intervals. By default, `paramci` computes confidence intervals for all distribution parameters.

paramci is meaningful only when pd is fitted to data, otherwise an empty array, [], is returned.

Example: 1


 ## Compute confidence intervals for parameters of a fitted Rayleigh
 ## distribution
 rand ("seed", 21);
 data = raylrnd (1, 1000, 1);
 pd_fitted = fitdist (data, "Rayleigh");
 ci = paramci (pd_fitted, "Alpha", 0.05)

 ## Use this to obtain confidence intervals for the estimated parameter (sigma),
 ## providing a range of plausible values given the data.

ci =

   0.9788
   1.0414

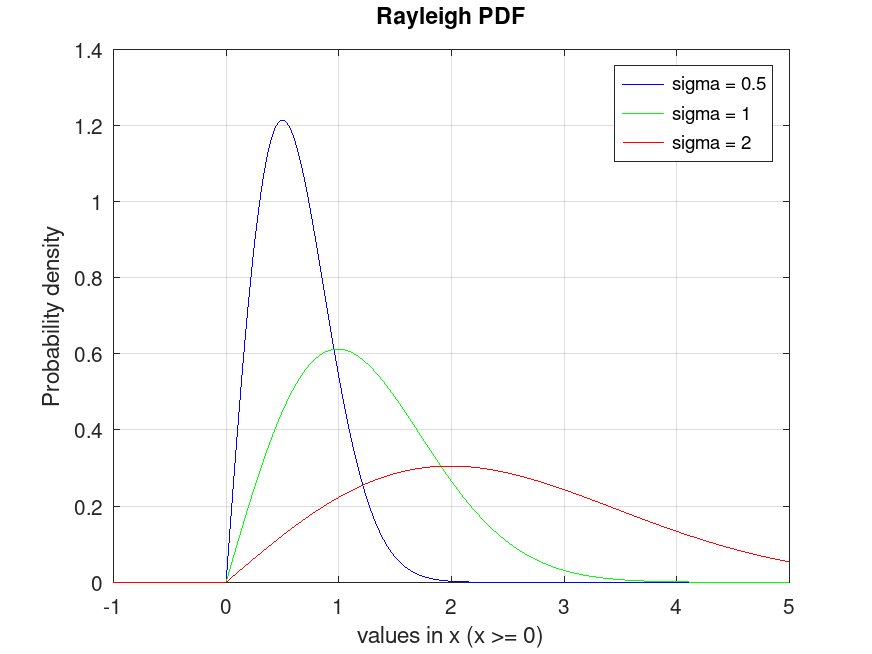
RayleighDistribution: y = pdf (pd, x)

y = pdf (pd, x) computes the PDF of the probability distribution object, pd, evaluated at the values in x.

Example: 1


 ## Plot various PDFs from the Rayleigh distribution
 x = -1:0.01:5;
 data1 = raylrnd (0.5, 10000, 1);
 data2 = raylrnd (1.0, 10000, 1);
 data3 = raylrnd (2.0, 10000, 1);
 pd1 = fitdist (data1, "Rayleigh");
 pd2 = fitdist (data2, "Rayleigh");
 pd3 = fitdist (data3, "Rayleigh");
 y1 = pdf (pd1, x);
 y2 = pdf (pd2, x);
 y3 = pdf (pd3, x);
 plot (x, y1, "-b", x, y2, "-g", x, y3, "-r")
 grid on
 legend ({"sigma = 0.5", "sigma = 1", "sigma = 2"}, ...
         "location", "northeast")
 title ("Rayleigh PDF")
 xlabel ("values in x (x >= 0)")
 ylabel ("Probability density")

 ## This visualizes the probability density function for Rayleigh
 ## distributions, showing the likelihood for nonnegative values.

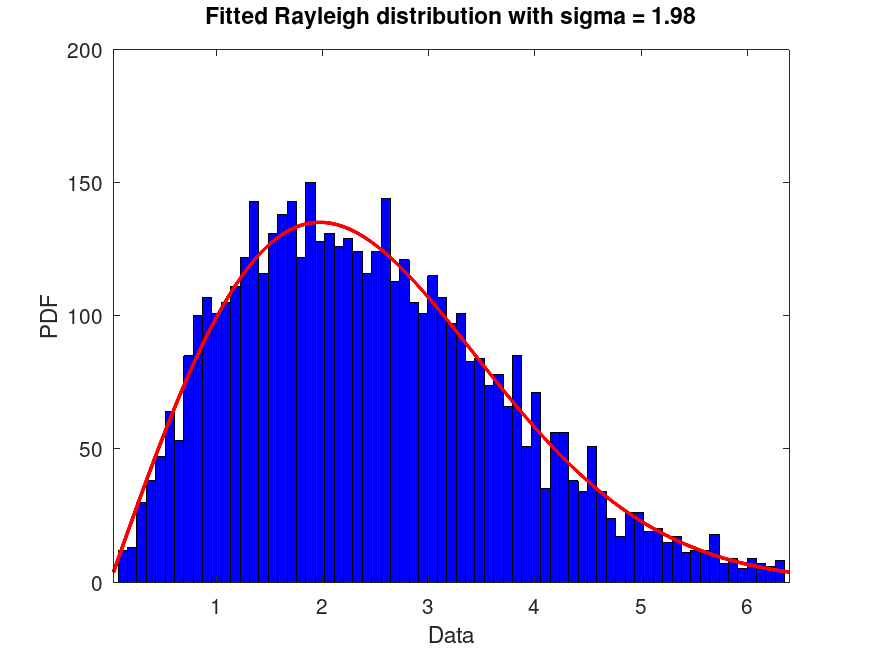
RayleighDistribution: plot (pd)
RayleighDistribution: plot (pd, Name, Value)
RayleighDistribution: h = plot (…)

plot (pd) plots a probability density function (PDF) of the probability distribution object pd. If pd contains data, which have been fitted by fitdist, the PDF is superimposed over a histogram of the data.

plot (pd, Name, Value) specifies additional options with the Name-Value pair arguments listed below.

`Name`		`Value`
`"PlotType"`		A character vector specifying the plot type. `"pdf"` plots the probability density function (PDF). When `pd` is fit to data, the PDF is superimposed on a histogram of the data. `"cdf"` plots the cumulative density function (CDF). When `pd` is fit to data, the CDF is superimposed over an empirical CDF. `"probability"` plots a probability plot using a CDF of the data and a CDF of the fitted probability distribution. This option is available only when `pd` is fitted to data.
`"Discrete"`		A logical scalar to specify whether to plot the PDF or CDF of a discrete distribution object as a line plot or a stem plot, by specifying `false` or `true`, respectively. By default, it is `true` for discrete distributions and `false` for continuous distributions. When `pd` is a continuous distribution object, option is ignored.
`"Parent"`		An axes graphics object for plot. If not specified, the `plot` function plots into the current axes or creates a new axes object if one does not exist.

h = plot (…) returns a graphics handle to the plotted objects.

Example: 1


 ## Create a Rayleigh distribution with fixed parameter sigma = 1 and plot its PDF.

 data = raylrnd (1, 10000, 1);
 pd = fitdist (data, "Rayleigh");
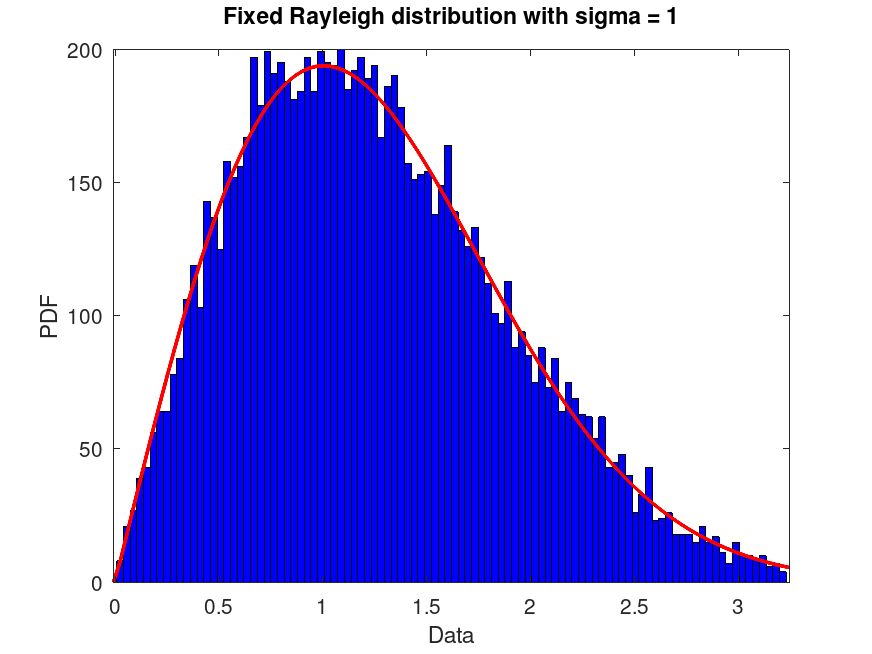
 plot (pd)
 title ("Fixed Rayleigh distribution with sigma = 1")

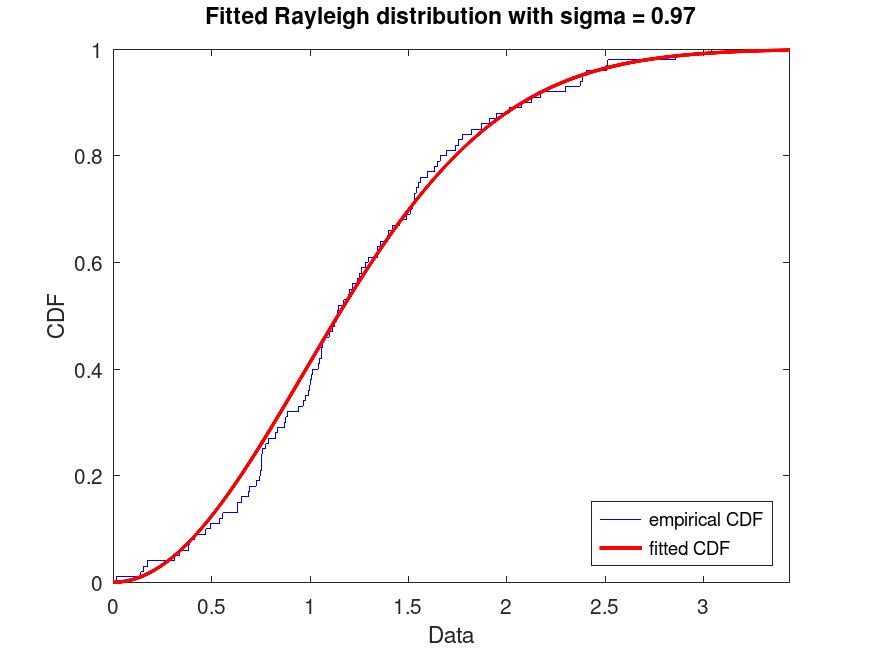
Example: 2


 ## Generate a data set of 100 random samples from a Rayleigh
 ## distribution with parameter sigma = 1. Fit a Rayleigh
 ## distribution to this data and plot its CDF superimposed over an empirical
 ## CDF.

 rand ("seed", 21);
 data = raylrnd (1, 100, 1);
 pd_fitted = fitdist (data, "Rayleigh");
 plot (pd_fitted, "PlotType", "cdf")
 txt = "Fitted Rayleigh distribution with sigma = %0.2f";
 title (sprintf (txt, pd_fitted.sigma))
 legend ({"empirical CDF", "fitted CDF"}, "location", "southeast")

 ## Use this to visualize the fitted CDF compared to the empirical CDF of the
 ## data, useful for assessing model fit.

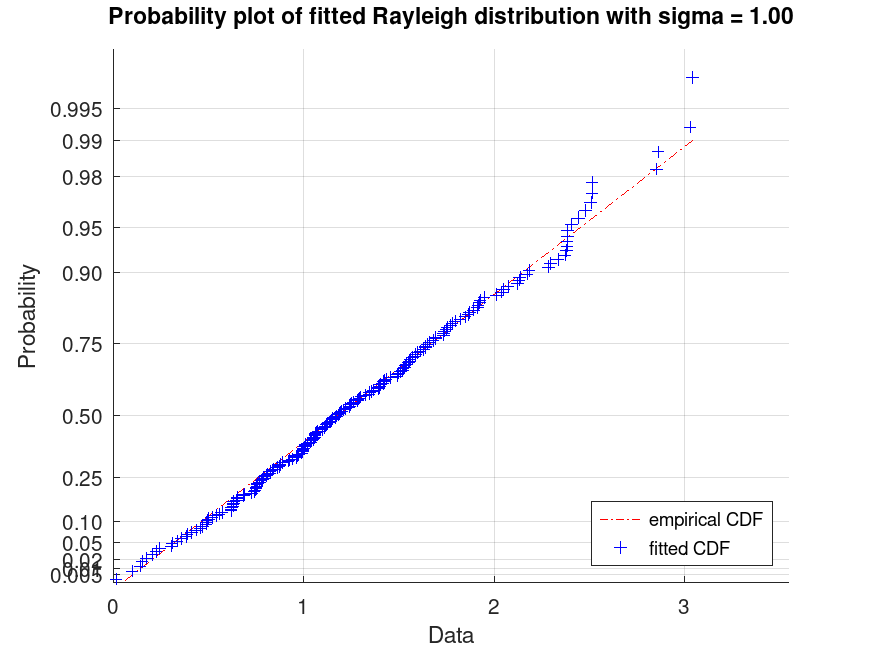
Example: 3


 ## Generate a data set of 200 random samples from a Rayleigh
 ## distribution with parameter sigma = 1. Display a probability
 ## plot for the Rayleigh distribution fit to the data.

 rand ("seed", 21);
 data = raylrnd (1, 200, 1);
 pd_fitted = fitdist (data, "Rayleigh");
 plot (pd_fitted, "PlotType", "probability")
 txt = strcat ("Probability plot of fitted Rayleigh", ...
               " distribution with sigma = %0.2f");
 title (sprintf (txt, pd_fitted.sigma))
 legend ({"empirical CDF", "fitted CDF"}, "location", "southeast")

 ## This creates a probability plot to compare the fitted distribution to the
 ## data, useful for checking if the Rayleigh model is appropriate.

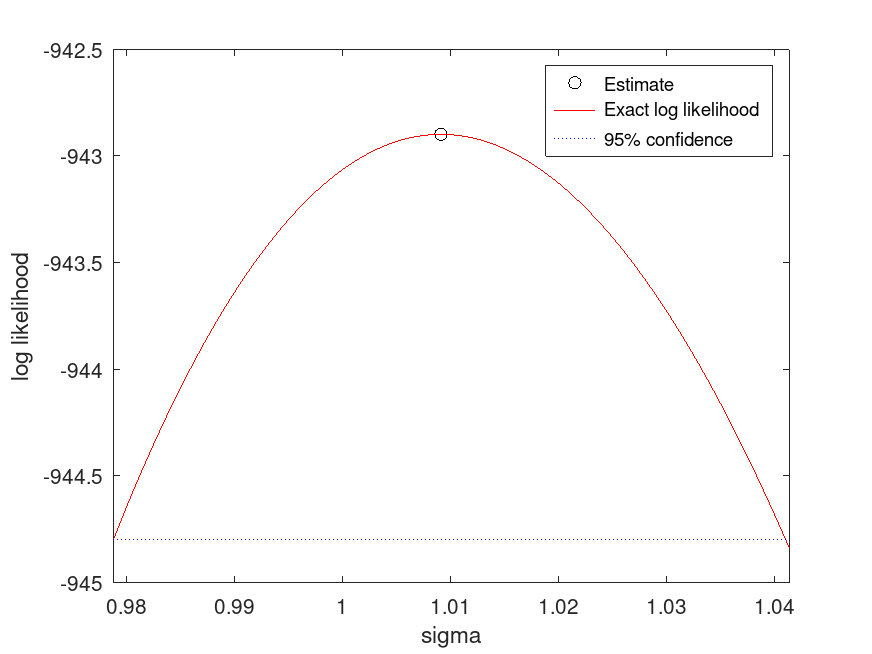
RayleighDistribution: [nlogL, param] = proflik (pd, pnum)
RayleighDistribution: [nlogL, param] = proflik (pd, pnum, "Display", display)
RayleighDistribution: [nlogL, param] = proflik (pd, pnum, setparam)
RayleighDistribution: [nlogL, param] = proflik (pd, pnum, setparam, "Display", display)

[nlogL, param] = proflik (pd, pnum) returns a vector nlogL of negative loglikelihood values and a vector param of corresponding parameter values for the parameter in the position indicated by pnum. By default, proflik uses the lower and upper bounds of the 95% confidence interval and computes 100 equispaced values for the selected parameter. pd must be fitted to data.

[nlogL, param] = proflik (pd, pnum, "Display", "on") also plots the profile likelihood against the default range of the selected parameter.

[nlogL, param] = proflik (pd, pnum, setparam) defines a user-defined range of the selected parameter.

[nlogL, param] = proflik (pd, pnum, setparam, "Display", "on") also plots the profile likelihood against the user-defined range of the selected parameter.

For the Rayleigh distribution, pnum = 1 selects the parameter sigma.

When opted to display the profile likelihood plot, proflik also plots the baseline loglikelihood computed at the lower bound of the 95% confidence interval and estimated maximum likelihood. The latter might not be observable if it is outside of the used-defined range of parameter values.

Example: 1


 ## Compute and plot the profile likelihood for the scale parameter of a fitted
 ## Rayleigh distribution
 rand ("seed", 21);
 data = raylrnd (1, 1000, 1);
 pd_fitted = fitdist (data, "Rayleigh");
 [nlogL, param] = proflik (pd_fitted, 1, "Display", "on");

 ## Use this to analyze the profile likelihood of the scale parameter (sigma),
 ## helping to understand the uncertainty in parameter estimates.

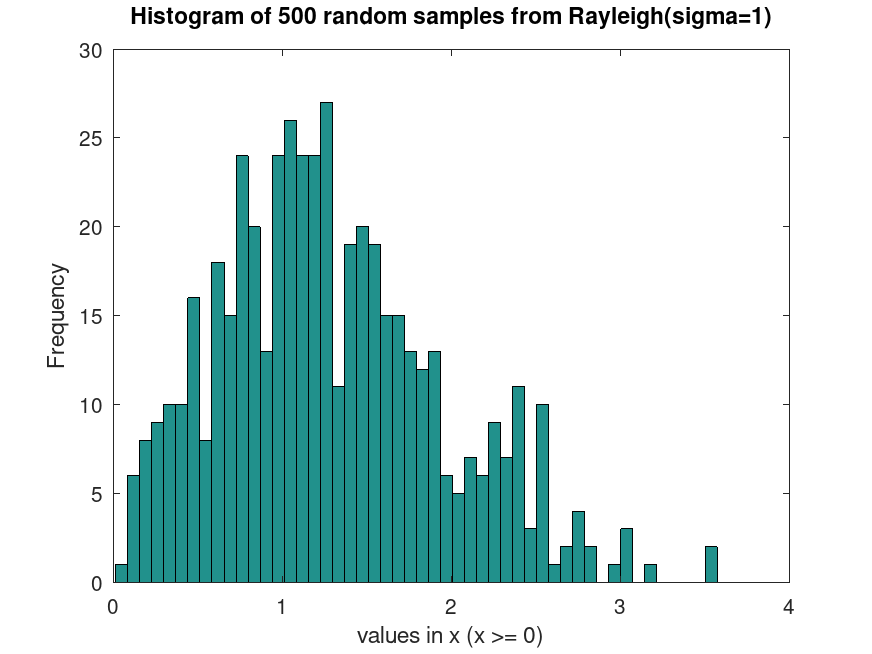
RayleighDistribution: r = random (pd)
RayleighDistribution: r = random (pd, rows)
RayleighDistribution: r = random (pd, rows, cols, …)
RayleighDistribution: r = random (pd, [sz])

r = random (pd) returns a random number from the distribution object pd.

When called with a single size argument, betarnd returns a square matrix with the dimension specified. When called with more than one scalar argument, the first two arguments are taken as the number of rows and columns and any further arguments specify additional matrix dimensions. The size may also be specified with a row vector of dimensions, sz.

Example: 1


 ## Generate random samples from a Rayleigh distribution
 rand ("seed", 21);
 samples = raylrnd (1, 500, 1);
 hist (samples, 50)
 title ("Histogram of 500 random samples from Rayleigh(sigma=1)")
 xlabel ("values in x (x >= 0)")
 ylabel ("Frequency")

 ## This generates random samples from a Rayleigh distribution, useful
 ## for simulating nonnegative data like envelope of narrowband signals.

RayleighDistribution: s = std (pd)

s = std (pd) computes the standard deviation of the probability distribution object, pd.

Example: 1


 ## Compute the standard deviation for a Rayleigh distribution
 data = raylrnd (1, 10000, 1);
 pd = fitdist (data, "Rayleigh");
 std_value = std (pd)

 ## Use this to calculate the standard deviation, which measures the variability
 ## in the nonnegative values of the distribution.

std_value = 0.6546

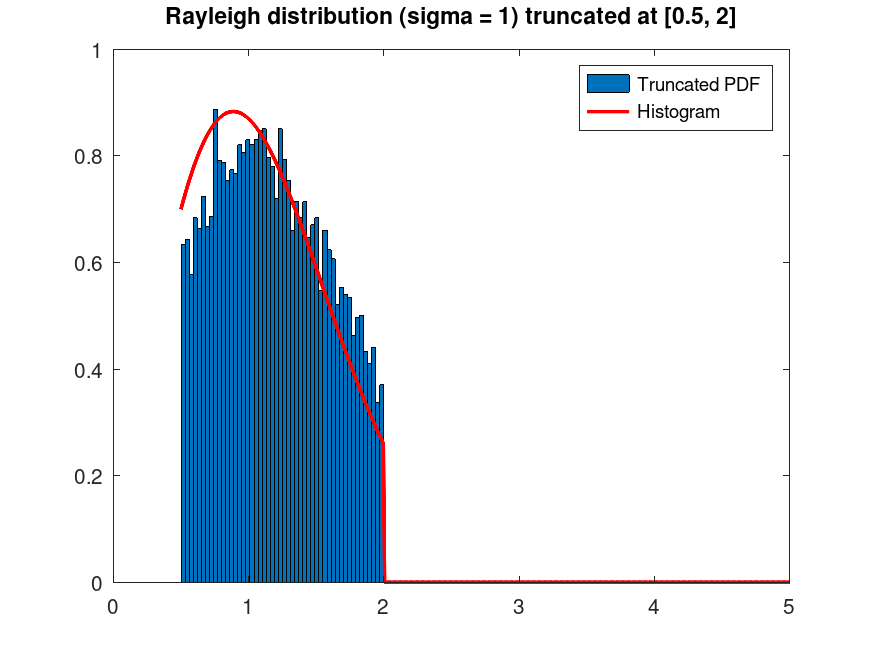
RayleighDistribution: t = truncate (pd, lower, upper)

t = truncate (pd, lower, upper) returns a probability distribution t, which is the probability distribution pd truncated to the specified interval with lower limit, lower, and upper limit, upper. If pd is fitted to data with fitdist, the returned probability distribution t is not fitted, does not contain any data or estimated values, and it is as it has been created with the makedist function, but it includes the truncation interval.

Example: 1


 ## Plot the PDF of a Rayleigh distribution, with parameter sigma = 1,
 ## truncated at [0.5, 2] intervals. Generate 10000 random
 ## samples from this truncated distribution and superimpose a histogram scaled
 ## accordingly

 rand ("seed", 21);
 data_all = raylrnd (1, 20000, 1);
 data = data_all(data_all >= 0.5 & data_all <= 2);
 data = data(1:10000);

 pd = fitdist (data, "Rayleigh");
 t = truncate (pd, 0.5, 2);

 [counts, centers] = hist (data, 50);
 bin_width = centers(2) - centers(1);
 bar (centers, counts / (sum (counts) * bin_width), 1);
 hold on;

 ## Plot histogram and truncated PDF
 x = linspace (0.5, 5, 500);
 y = pdf (t, x);
 plot (x, y, "r", "linewidth", 2);
 title ("Rayleigh distribution (sigma = 1) truncated at [0.5, 2]")
 legend ("Truncated PDF", "Histogram")

 ## This demonstrates truncating a Rayleigh distribution to a specific
 ## range and visualizing the resulting distribution with random samples.

RayleighDistribution: v = var (pd)

v = var (pd) computes the variance of the probability distribution object, pd.

Example: 1


 ## Compute the variance for a Rayleigh distribution
 data = raylrnd (1, 10000, 1);
 pd = fitdist (data, "Rayleigh");
 var_value = var (pd)

 ## Use this to calculate the variance, which quantifies the spread of the
 ## nonnegative values in the distribution.

var_value = 0.4250

Examples

 pd_fixed = makedist ("Rayleigh", "sigma", 2)
 rand ("seed", 2);
 data = random (pd_fixed, 5000, 1);
 pd_fitted = fitdist (data, "Rayleigh")
 plot (pd_fitted)
 msg = "Fitted Rayleigh distribution with sigma = %0.2f";
 title (sprintf (msg, pd_fitted.sigma))

pd_fixed =
  RayleighDistribution

  Rayleigh distribution
    sigma = 2

pd_fitted =
  RayleighDistribution

  Rayleigh distribution
    sigma = 1.97536   [1.94836, 2.00313]

Categories &

Functions List

Clustering

Clustering

Classification Classes

Classification Classes

Clustering Classes

Clustering Classes

Regression Classes

Regression Classes

Data Manipulation

Data Manipulation

Descriptive Statistics

Descriptive Statistics

Distribution Classes

Distribution Classes

Distribution Fitting

Distribution Fitting

Distribution Functions

Distribution Functions

Distribution Statistics

Distribution Statistics

Distribution Wrappers

Distribution Wrappers

Experimental Design

Experimental Design

Machine Learning

Machine Learning

Model Fitting

Model Fitting

Hypothesis Testing

Hypothesis Testing

I/O

I/O

Plotting

Plotting

Regression

Regression

Transforms

Transforms

Class Definition: RayleighDistribution

statistics: RayleighDistribution

Properties

sigma

Example: 1

DistributionName

NumParameters

ParameterNames

ParameterDescription

ParameterValues

ParameterCovariance

ParameterIsFixed

Truncation

IsTruncated

InputData

Methods

cdf

RayleighDistribution: p = cdf (pd, x)

RayleighDistribution: p = cdf (pd, x, "upper")

Example: 1

icdf

RayleighDistribution: x = icdf (pd, p)

Example: 1

iqr

RayleighDistribution: r = iqr (pd)

Example: 1

mean

RayleighDistribution: m = mean (pd)

Example: 1

median

RayleighDistribution: m = median (pd)

Example: 1

negloglik

RayleighDistribution: nlogL = negloglik (pd)

Example: 1

paramci

RayleighDistribution: ci = paramci (pd)

RayleighDistribution: ci = paramci (pd, Name, Value)

Example: 1

pdf

Class Definition: `RayleighDistribution`

`sigma`

`DistributionName`

`NumParameters`

`ParameterNames`

`ParameterDescription`

`ParameterValues`

`ParameterCovariance`

`ParameterIsFixed`

`Truncation`

`IsTruncated`

`InputData`

`cdf`

`RayleighDistribution: p = cdf (pd, x)`

`RayleighDistribution: p = cdf (pd, x, "upper")`

`icdf`

`RayleighDistribution: x = icdf (pd, p)`

`iqr`

`RayleighDistribution: r = iqr (pd)`

`mean`

`RayleighDistribution: m = mean (pd)`

`median`

`RayleighDistribution: m = median (pd)`

`negloglik`

`RayleighDistribution: nlogL = negloglik (pd)`

`paramci`

`RayleighDistribution: ci = paramci (pd)`

`RayleighDistribution: ci = paramci (pd, Name, Value)`

`pdf`

`RayleighDistribution: y = pdf (pd, x)`

`plot`

`RayleighDistribution: plot (pd)`

`RayleighDistribution: plot (pd, Name, Value)`

`RayleighDistribution: h = plot (…)`

`proflik`

`RayleighDistribution: [nlogL, param] = proflik (pd, pnum)`

`RayleighDistribution: [nlogL, param] = proflik (pd, pnum, "Display", display)`

`RayleighDistribution: [nlogL, param] = proflik (pd, pnum, setparam)`

`RayleighDistribution: [nlogL, param] = proflik (pd, pnum, setparam, "Display", display)`

`random`

`RayleighDistribution: r = random (pd)`

`RayleighDistribution: r = random (pd, rows)`

`RayleighDistribution: r = random (pd, rows, cols, …)`

`RayleighDistribution: r = random (pd, [sz])`

`std`

`RayleighDistribution: s = std (pd)`

`truncate`

`RayleighDistribution: t = truncate (pd, lower, upper)`

`var`

`RayleighDistribution: v = var (pd)`