Categories &

Functions List

Function Reference: gamfit

statistics: paramhat = gamfit (x)
statistics: [paramhat, paramci] = gamfit (x)
statistics: [paramhat, paramci] = gamfit (x, alpha)
statistics: […] = gamfit (x, alpha, censor)
statistics: […] = gamfit (x, alpha, censor, freq)
statistics: […] = gamfit (x, alpha, censor, freq, options)

Estimate parameters and confidence intervals for the Gamma distribution.

paramhat = gamfit (x) returns the maximum likelihood estimates of the parameters of the Gamma distribution given the data in x. paramhat(1) is the shape parameter, a, and paramhat(2) is the scale parameter, b.

[paramhat, paramci] = gamfit (x) returns the 95% confidence intervals for the parameter estimates.

[…] = gamfit (x, alpha) also returns the 100 * (1 - alpha) percent confidence intervals for the parameter estimates. By default, the optional argument alpha is 0.05 corresponding to 95% confidence intervals. Pass in [] for alpha to use the default values.

[…] = gamfit (x, alpha, censor) accepts a boolean vector, censor, of the same size as x with 1s for observations that are right-censored and 0s for observations that are observed exactly. By default, or if left empty, censor = zeros (size (x)).

[…] = gamfit (x, alpha, censor, freq) accepts a frequency vector, freq, of the same size as x. freq typically contains integer frequencies for the corresponding elements in x, but it can contain any non-integer non-negative values. By default, or if left empty, freq = ones (size (x)).

[…] = gamfit (…, options) specifies control parameters for the iterative algorithm used to compute the maximum likelihood estimates. options is a structure with the following field and its default value:

  • options.Display = "off"
  • options.MaxFunEvals = 400
  • options.MaxIter = 200
  • options.TolX = 1e-6

OCTAVE/MATLAB use the alternative parameterization given by the pair α, β, i.e. shape a and scale b. In Wikipedia, the two common parameterizations use the pairs k, θ, as shape and scale, and α, β, as shape and rate, respectively. The parameter names a and b used here (for MATLAB compatibility) correspond to the parameter notation k, θ instead of the α, β as reported in Wikipedia.

Further information about the Gamma distribution can be found at https://en.wikipedia.org/wiki/Gamma_distribution

See also: gamcdf, gampdf, gaminv, gamrnd, gamlike

Source Code: gamfit

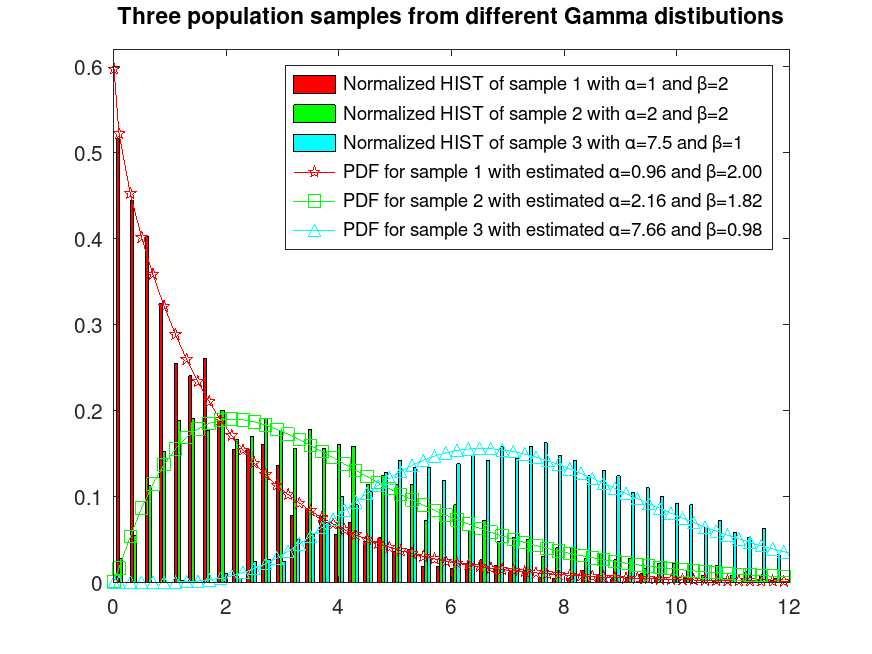
Example: 1

  

 ## Sample 3 populations from different Gamma distibutions
 randg ("seed", 5);    # for reproducibility
 r1 = gamrnd (1, 2, 2000, 1);
 randg ("seed", 2);    # for reproducibility
 r2 = gamrnd (2, 2, 2000, 1);
 randg ("seed", 7);    # for reproducibility
 r3 = gamrnd (7.5, 1, 2000, 1);
 r = [r1, r2, r3];

 ## Plot them normalized and fix their colors
 hist (r, 75, 4);
 h = findobj (gca, "Type", "patch");
 set (h(1), "facecolor", "c");
 set (h(2), "facecolor", "g");
 set (h(3), "facecolor", "r");
 ylim ([0, 0.62]);
 xlim ([0, 12]);
 hold on

 ## Estimate their α and β parameters
 a_bA = gamfit (r(:,1));
 a_bB = gamfit (r(:,2));
 a_bC = gamfit (r(:,3));

 ## Plot their estimated PDFs
 x = [0.01,0.1:0.2:18];
 y = gampdf (x, a_bA(1), a_bA(2));
 plot (x, y, "-pr");
 y = gampdf (x, a_bB(1), a_bB(2));
 plot (x, y, "-sg");
 y = gampdf (x, a_bC(1), a_bC(2));
 plot (x, y, "-^c");
 hold off
 legend ({"Normalized HIST of sample 1 with α=1 and β=2", ...
          "Normalized HIST of sample 2 with α=2 and β=2", ...
          "Normalized HIST of sample 3 with α=7.5 and β=1", ...
          sprintf("PDF for sample 1 with estimated α=%0.2f and β=%0.2f", ...
                  a_bA(1), a_bA(2)), ...
          sprintf("PDF for sample 2 with estimated α=%0.2f and β=%0.2f", ...
                  a_bB(1), a_bB(2)), ...
          sprintf("PDF for sample 3 with estimated α=%0.2f and β=%0.2f", ...
                  a_bC(1), a_bC(2))})
 title ("Three population samples from different Gamma distibutions")
 hold off
plotted figure