Categories &

Functions List

Class Definition: RegressionGAM

statistics: obj = RegressionGAM (X, Y)
statistics: obj = RegressionGAM (…, name, value)

Create a RegressionGAM class object containing a Generalised Additive Model (GAM) for regression.

A RegressionGAM class object can store the predictors and response data along with various parameters for the GAM model. It is recommended to use the fitrgam function to create a RegressionGAM object.

obj = RegressionGAM (X, Y) returns an object of class RegressionGAM, with matrix X containing the predictor data and vector Y containing the continuous response data.

  • X must be a N×P numeric matrix of input data where rows correspond to observations and columns correspond to features or variables. X will be used to train the GAM model.
  • Y must be N×1 numeric vector containing the response data corresponding to the predictor data in X. Y must have same number of rows as X.

obj = RegressionGAM (…, name, value) returns an object of class RegressionGAM with additional properties specified by Name-Value pair arguments listed below.

NameValue
"predictors"Predictor Variable names, specified as a row vector cell of strings with the same length as the columns in X. If omitted, the program will generate default variable names (x1, x2, ..., xn) for each column in X.
"responsename"Response Variable Name, specified as a string. If omitted, the default value is "Y".
"formula"a model specification given as a string in the form "Y ~ terms" where Y represents the reponse variable and terms the predictor variables. The formula can be used to specify a subset of variables for training model. For example: "Y ~ x1 + x2 + x3 + x4 + x1:x2 + x2:x3" specifies four linear terms for the first four columns of for predictor data, and x1:x2 and x2:x3 specify the two interaction terms for 1st-2nd and 3rd-4th columns respectively. Only these terms will be used for training the model, but X must have at least as many columns as referenced in the formula. If Predictor Variable names have been defined, then the terms in the formula must reference to those. When "formula" is specified, all terms used for training the model are referenced in the IntMatrix field of the obj class object as a matrix containing the column indexes for each term including both the predictors and the interactions used.
"interactions"a logical matrix, a positive integer scalar, or the string "all" for defining the interactions between predictor variables. When given a logical matrix, it must have the same number of columns as X and each row corresponds to a different interaction term combining the predictors indexed as true. Each interaction term is appended as a column vector after the available predictor column in X. When "all" is defined, then all possible combinations of interactions are appended in X before training. At the moment, parsing a positive integer has the same effect as the "all" option. When "interactions" is specified, only the interaction terms appended to X are referenced in the IntMatrix field of the obj class object.
"knots"a scalar or a row vector with the same columns as X. It defines the knots for fitting a polynomial when training the GAM. As a scalar, it is expanded to a row vector. The default value is 5, hence expanded to ones (1, columns (X)) * 5. You can parse a row vector with different number of knots for each predictor variable to be fitted with, although not recommended.
"order"a scalar or a row vector with the same columns as X. It defines the order of the polynomial when training the GAM. As a scalar, it is expanded to a row vector. The default values is 3, hence expanded to ones (1, columns (X)) * 3. You can parse a row vector with different number of polynomial order for each predictor variable to be fitted with, although not recommended.
"dof"a scalar or a row vector with the same columns as X. It defines the degrees of freedom for fitting a polynomial when training the GAM. As a scalar, it is expanded to a row vector. The default value is 8, hence expanded to ones (1, columns (X)) * 8. You can parse a row vector with different degrees of freedom for each predictor variable to be fitted with, although not recommended.
"tol"a positive scalar to set the tolerance for covergence during training. By defaul, it is set to 1e-3.

You can parse either a "formula" or an "interactions" optional parameter. Parsing both parameters will result an error. Accordingly, you can only pass up to two parameters among "knots", "order", and "dof" to define the required polynomial for training the GAM model.

See also: fitrgam, regress, regress_gp

Source Code: RegressionGAM

Method: predict

RegressionGAM: yFit = predict (obj, Xfit)
RegressionGAM: yFit = predict (…, Name, Value)
RegressionGAM: [yFit, ySD, yInt] = predict (…)

Predict new data points using generalized additive model regression object.

yFit = predict (obj, Xfit returns a vector of predicted responses, yFit, for the predictor data in matrix Xfit based on the Generalized Additive Model in obj. Xfit must have the same number of features/variables as the training data in obj.

  • obj must be a RegressionGAM class object.

[yFit, ySD, yInt] = predict (obj, Xfit also returns the standard deviations, ySD, and prediction intervals, yInt, of the response variable yFit, evaluated at each observation in the predictor data Xfit.

yFit = predict (…, Name, Value) returns the aforementioned results with additional properties specified by Name-Value pair arguments listed below.

NameValue
"alpha"significance level of the prediction intervals yInt, specified as scalar in range [0,1]. The default value is 0.05, which corresponds to 95% prediction intervals.
"includeinteractions"a boolean flag to include interactions to predict new values based on Xfit. By default, "includeinteractions" is true when the GAM model in obj contains a obj.Formula or obj.Interactions fields. Otherwise, is set to false. If set to true when no interactions are present in the trained model, it will result to an error. If set to false when using a model that includes interactions, the predictions will be made on the basic model without any interaction terms. This way you can make predictions from the same GAM model without having to retrain it.

See also: fitrgam, RegressionGAM

Method: savemodel

RegressionGAM: savemodel (obj, filename)

Save a RegressionGAM object.

savemodel (obj, filename) saves a RegressionGAM object into a file defined by filename.

See also: loadmodel, fitrgam, RegressionGAM

Example: 1

  

 ## Train a RegressionGAM Model for synthetic values
 f1 = @(x) cos (3 * x);
 f2 = @(x) x .^ 3;
 x1 = 2 * rand (50, 1) - 1;
 x2 = 2 * rand (50, 1) - 1;
 y = f1(x1) + f2(x2);
 y = y + y .* 0.2 .* rand (50,1);
 X = [x1, x2];
 a = fitrgam (X, y, "tol", 1e-3)

a =

  RegressionGAM object with properties:

            BaseModel: [1x1 struct]
                  DoF: [1x2 double]
              Formula: [0x0 double]
            IntMatrix: [0x0 double]
         Interactions: [0x0 double]
                Knots: [1x2 double]
            ModelwInt: [0x0 double]
      NumObservations: [1x1 double]
        NumPredictors: [1x1 double]
                Order: [1x2 double]
       PredictorNames: [1x2 cell]
         ResponseName: Y
             RowsUsed: [50x1 double]
                  Tol: [1x1 double]
                    X: [50x2 double]
                    Y: [50x1 double]

Example: 2

  

 ## Declare two different functions
 f1 = @(x) cos (3 * x);
 f2 = @(x) x .^ 3;

 ## Generate 80 samples for f1 and f2
 x = [-4*pi:0.1*pi:4*pi-0.1*pi]';
 X1 = f1 (x);
 X2 = f2 (x);

 ## Create a synthetic response by adding noise
 rand ("seed", 3);
 Ytrue = X1 + X2;
 Y = Ytrue + Ytrue .* 0.2 .* rand (80,1);

 ## Assemble predictor data
 X = [X1, X2];

 ## Train the GAM and test on the same data
 a = fitrgam (X, Y, "order", [5, 5]);
 [ypred, ySDsd, yInt] = predict (a, X);

 ## Plot the results
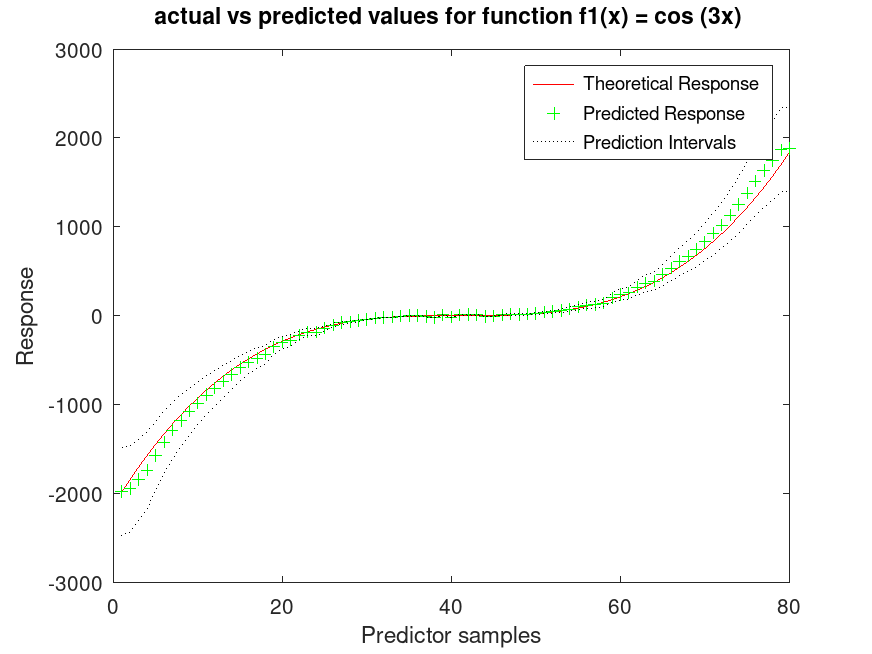
 figure
 [sortedY, indY] = sort (Ytrue);
 plot (sortedY, "r-");
 xlim ([0, 80]);
 hold on
 plot (ypred(indY), "g+")
 plot (yInt(indY,1), "k:")
 plot (yInt(indY,2), "k:")
 xlabel ("Predictor samples");
 ylabel ("Response");
 title ("actual vs predicted values for function f1(x) = cos (3x) ");
 legend ({"Theoretical Response", "Predicted Response", "Prediction Intervals"});

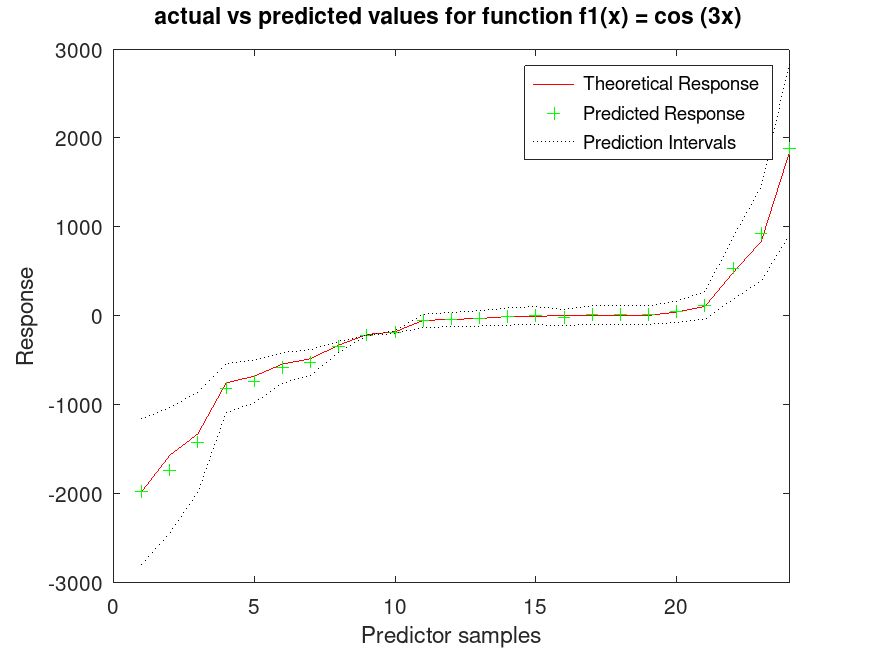
 ## Use 30% Holdout partitioning for training and testing data
 C = cvpartition (80, "HoldOut", 0.3);
 [ypred, ySDsd, yInt] = predict (a, X(test(C),:));

 ## Plot the results
 figure
 [sortedY, indY] = sort (Ytrue(test(C)));
 plot (sortedY, 'r-');
 xlim ([0, sum(test(C))]);
 hold on
 plot (ypred(indY), "g+")
 plot (yInt(indY,1),'k:')
 plot (yInt(indY,2),'k:')
 xlabel ("Predictor samples");
 ylabel ("Response");
 title ("actual vs predicted values for function f1(x) = cos (3x) ");
 legend ({"Theoretical Response", "Predicted Response", "Prediction Intervals"});
plotted figure

plotted figure