Statistics: UniformDistribution

Class Definition: `UniformDistribution`

statistics: UniformDistribution

Continuous uniform probability distribution object.

A UniformDistribution object consists of parameters, a model description, and sample data for a uniform probability distribution.

The uniform distribution is a continuous probability distribution that models random variables that are equally likely to take any value within a specified interval defined by the lower limit Lower and upper limit Upper.

There are several ways to create a UniformDistribution object.

Fit a distribution to data using the fitdist function.
Create a distribution with fixed parameter values using the makedist function.
Use the constructor UniformDistribution (Lower, Upper) to create a uniform distribution with fixed parameter values Lower and Upper.

It is highly recommended to use fitdist and makedist functions to create probability distribution objects, instead of the class constructor.

Further information about the continuous uniform distribution can be found at https://en.wikipedia.org/wiki/Continuous_uniform_distribution

See also: fitdist, makedist, unifcdf, unifinv, unifpdf, unifrnd, unifit, unifstat

Source Code: UniformDistribution

Properties

A scalar value characterizing the lower bound of the uniform distribution. You can access the Lower property using dot name assignment.

Example: 1


 ## Create a Uniform distribution with default parameters
 pd = makedist ("Uniform", "Lower", 2, "Upper", 5);

 ## Query parameter 'Lower' (lower limit parameter)
 pd.Lower

 ## Set parameter 'Lower'
 pd.Lower = 2

 ## Use this to initialize or modify the lower bound of a Uniform distribution.
 ## The lower limit must be a real scalar less than the upper limit, useful for
 ## defining the range of a uniform variable, such as random measurements or time intervals.

ans = 2
pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower = 2
    Upper = 5

Example: 2


 ## Create a Uniform distribution object by calling its constructor
 pd = UniformDistribution (1, 10)

 ## Query parameter 'Lower'
 pd.Lower

 ## This demonstrates direct construction with a specific lower limit, ideal for
 ## modeling data uniformly distributed over a known interval, such as random selections.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower =  1
    Upper = 10

ans = 1

A scalar value characterizing the upper bound of the uniform distribution. You can access the Upper property using dot name assignment.

Example: 1


 ## Create a Uniform distribution with default parameters
 pd = makedist ("Uniform")

 ## Query parameter 'Upper' (upper limit parameter)
 pd.Upper

 ## Set parameter 'Upper'
 pd.Upper = 8

 ## Use this to initialize or modify the upper bound of a Uniform distribution.
 ## The upper limit must be a real scalar greater than the lower limit, controlling
 ## the range of the distribution.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower = 0
    Upper = 1

ans = 1
pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower = 0
    Upper = 8

Example: 2


 ## Create a Uniform distribution object by calling its constructor
 pd = UniformDistribution (1, 10)

 ## Query parameter 'Upper'
 pd.Upper

 ## This shows how to set the upper limit directly via the constructor, useful
 ## for defining the maximum value in a uniform distribution.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower =  1
    Upper = 10

ans = 10

A character vector specifying the name of the probability distribution object. This property is read-only.

A scalar integer value specifying the number of parameters characterizing the probability distribution. This property is read-only.

A $2×1$ cell array of character vectors with each element containing the name of a distribution parameter. This property is read-only.

A $2×1$ cell array of character vectors with each element containing a short description of a distribution parameter. This property is read-only.

A $2×1$ numeric vector containing the values of the distribution parameters. This property is read-only. You can change the distribution parameters by assigning new values to the Lower and Upper properties.

A $1×2$ numeric vector specifying the truncation interval for the probability distribution. First element contains the lower boundary, second element contains the upper boundary. This property is read-only. You can only truncate a probability distribution with the truncate method.

A logical scalar value specifying whether a probability distribution is truncated or not. This property is read-only.

Methods

UniformDistribution: p = cdf (pd, x)
UniformDistribution: p = cdf (pd, x, "upper")

p = cdf (pd, x) computes the CDF of the probability distribution object, pd, evaluated at the values in x.

p = cdf (…, "upper") returns the complement of the CDF of the probability distribution object, pd, evaluated at the values in x.

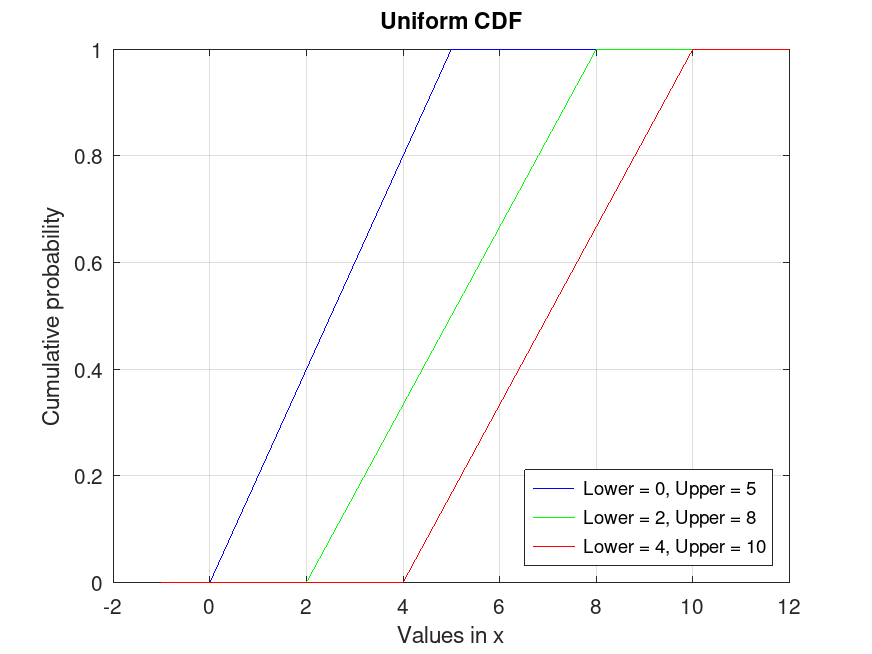
Example: 1


 ## Plot various CDFs from the Uniform distribution
 x = -1:0.01:12;
 pd1 = makedist ("Uniform", "Lower", 0, "Upper", 5);
 pd2 = makedist ("Uniform", "Lower", 2, "Upper", 8);
 pd3 = makedist ("Uniform", "Lower", 4, "Upper", 10);
 p1 = cdf (pd1, x);
 p2 = cdf (pd2, x);
 p3 = cdf (pd3, x);
 plot (x, p1, "-b", x, p2, "-g", x, p3, "-r")
 grid on
 legend ({"Lower = 0, Upper = 5", "Lower = 2, Upper = 8", "Lower = 4, Upper = 10"}, ...
         "location", "southeast")
 title ("Uniform CDF")
 xlabel ("Values in x")
 ylabel ("Cumulative probability")

 ## Use this to compute and visualize the cumulative distribution function
 ## for different Uniform distributions, showing how probability accumulates
 ## over the defined interval, useful in probability assessments or simulations.

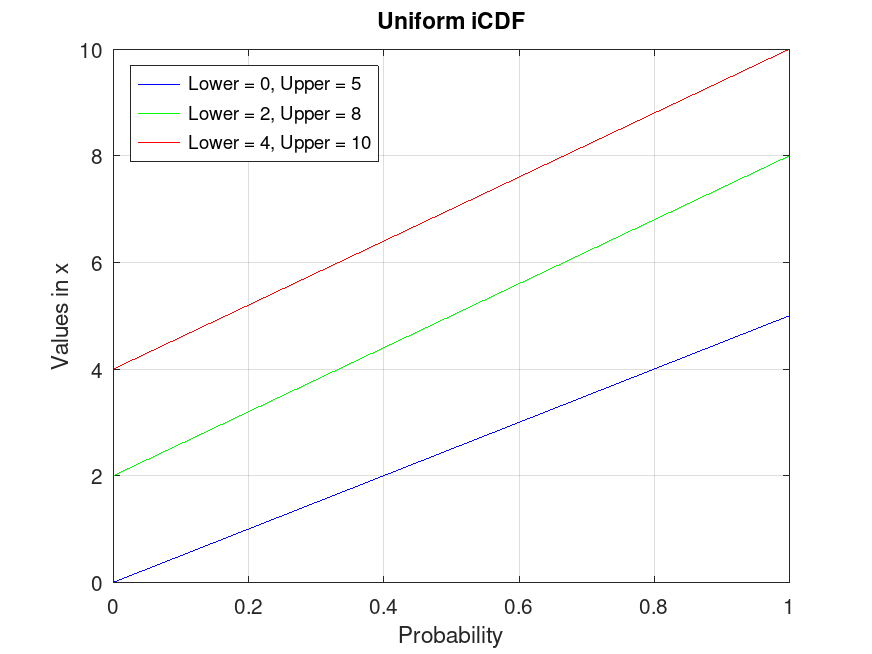
UniformDistribution: x = icdf (pd, p)

x = icdf (pd, p) computes the quantile (the inverse of the CDF) of the probability distribution object, pd, evaluated at the values in p.

Example: 1


 ## Plot various iCDFs from the Uniform distribution
 p = 0.001:0.001:0.999;
 pd1 = makedist ("Uniform", "Lower", 0, "Upper", 5);
 pd2 = makedist ("Uniform", "Lower", 2, "Upper", 8);
 pd3 = makedist ("Uniform", "Lower", 4, "Upper", 10);
 x1 = icdf (pd1, p);
 x2 = icdf (pd2, p);
 x3 = icdf (pd3, p);
 plot (p, x1, "-b", p, x2, "-g", p, x3, "-r")
 grid on
 legend ({"Lower = 0, Upper = 5", "Lower = 2, Upper = 8", "Lower = 4, Upper = 10"}, ...
         "location", "northwest")
 title ("Uniform iCDF")
 xlabel ("Probability")
 ylabel ("Values in x")

 ## This demonstrates the inverse CDF (quantiles) for Uniform distributions,
 ## useful for finding values corresponding to given probabilities, such as
 ## thresholds in uniform sampling.

UniformDistribution: r = iqr (pd)

r = iqr (pd) computes the interquartile range of the probability distribution object, pd.

Example: 1


 ## Compute the interquartile range for a Uniform distribution
 pd = makedist ("Uniform", "Lower", 0, "Upper", 10)
 iqr_value = iqr (pd)

 ## Use this to calculate the interquartile range, which measures the spread
 ## of the middle 50% of the distribution, helpful for understanding central
 ## variability in uniformly distributed data.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower =  0
    Upper = 10

iqr_value = 5

UniformDistribution: m = mean (pd)

m = mean (pd) computes the mean of the probability distribution object, pd.

Example: 1


 ## Compute the mean for different Uniform distributions
 pd1 = makedist ("Uniform", "Lower", 0, "Upper", 5);
 pd2 = makedist ("Uniform", "Lower", 2, "Upper", 8);
 mean1 = mean (pd1)
 mean2 = mean (pd2)

 ## This shows how to compute the expected value for Uniform distributions
 ## with different bounds, representing the average value within the interval.

mean1 = 2.5000
mean2 = 5

UniformDistribution: m = median (pd)

m = median (pd) computes the median of the probability distribution object, pd.

Example: 1


 ## Compute the median for different Uniform distributions
 pd1 = makedist ("Uniform", "Lower", 0, "Upper", 5);
 pd2 = makedist ("Uniform", "Lower", 2, "Upper", 8);
 median1 = median (pd1)
 median2 = median (pd2)

 ## Use this to find the median value, which splits the distribution
 ## into two equal probability halves, useful for central tendency in uniform data.

median1 = 2.5000
median2 = 5

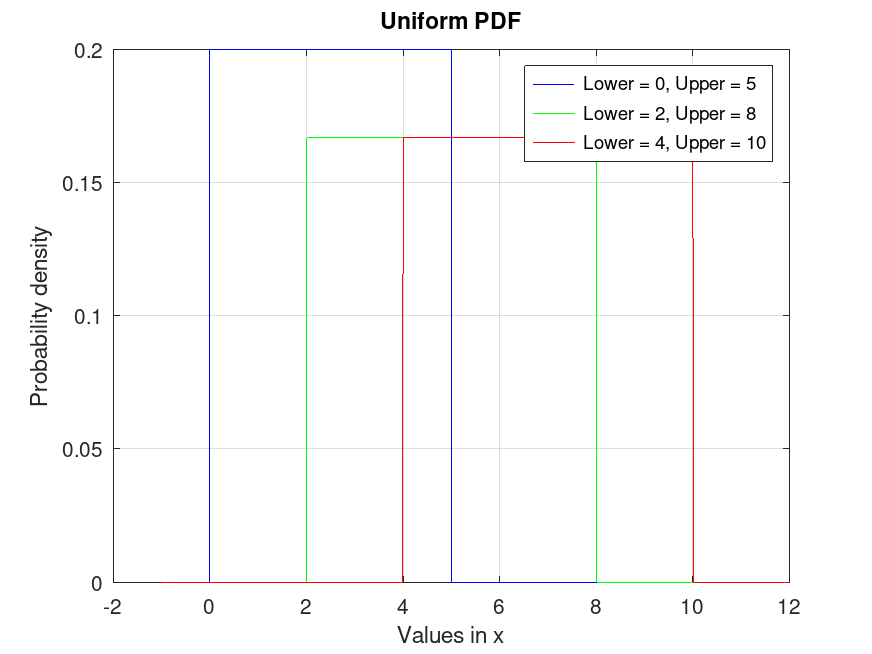
UniformDistribution: y = pdf (pd, x)

y = pdf (pd, x) computes the PDF of the probability distribution object, pd, evaluated at the values in x.

Example: 1


 ## Plot various PDFs from the Uniform distribution
 x = -1:0.01:12;
 pd1 = makedist ("Uniform", "Lower", 0, "Upper", 5);
 pd2 = makedist ("Uniform", "Lower", 2, "Upper", 8);
 pd3 = makedist ("Uniform", "Lower", 4, "Upper", 10);
 y1 = pdf (pd1, x);
 y2 = pdf (pd2, x);
 y3 = pdf (pd3, x);
 plot (x, y1, "-b", x, y2, "-g", x, y3, "-r")
 grid on
 legend ({"Lower = 0, Upper = 5", "Lower = 2, Upper = 8", "Lower = 4, Upper = 10"}, ...
         "location", "northeast")
 title ("Uniform PDF")
 xlabel ("Values in x")
 ylabel ("Probability density")

 ## This visualizes the probability density function for Uniform distributions,
 ## showing the constant likelihood within the defined interval.

UniformDistribution: plot (pd)
UniformDistribution: plot (pd, Name, Value)
UniformDistribution: h = plot (…)

plot (pd) plots a probability density function (PDF) of the probability distribution object pd. If pd contains data, which have been fitted by fitdist, the PDF is superimposed over a histogram of the data.

plot (pd, Name, Value) specifies additional options with the Name-Value pair arguments listed below.

`Name`		`Value`
`"PlotType"`		A character vector specifying the plot type. `"pdf"` plots the probability density function (PDF). When `pd` is fit to data, the PDF is superimposed on a histogram of the data. `"cdf"` plots the cumulative density function (CDF). When `pd` is fit to data, the CDF is superimposed over an empirical CDF. `"probability"` plots a probability plot using a CDF of the data and a CDF of the fitted probability distribution. This option is available only when `pd` is fitted to data.
`"Discrete"`		A logical scalar to specify whether to plot the PDF or CDF of a discrete distribution object as a line plot or a stem plot, by specifying `false` or `true`, respectively. By default, it is `true` for discrete distributions and `false` for continuous distributions. When `pd` is a continuous distribution object, option is ignored.
`"Parent"`		An axes graphics object for plot. If not specified, the `plot` function plots into the current axes or creates a new axes object if one does not exist.

h = plot (…) returns a graphics handle to the plotted objects.

Example: 1


 ## Create a Uniform distribution with fixed parameters Lower = 0 and Upper = 5
 ## and plot its PDF.
 pd = makedist ("Uniform", "Lower", 0, "Upper", 5)
 plot (pd)
 title ("Uniform distribution with Lower = 0 and Upper = 5")

 ## Use this to visualize the PDF of a Uniform distribution with fixed bounds,
 ## useful for understanding the uniform probability density.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower = 0
    Upper = 5

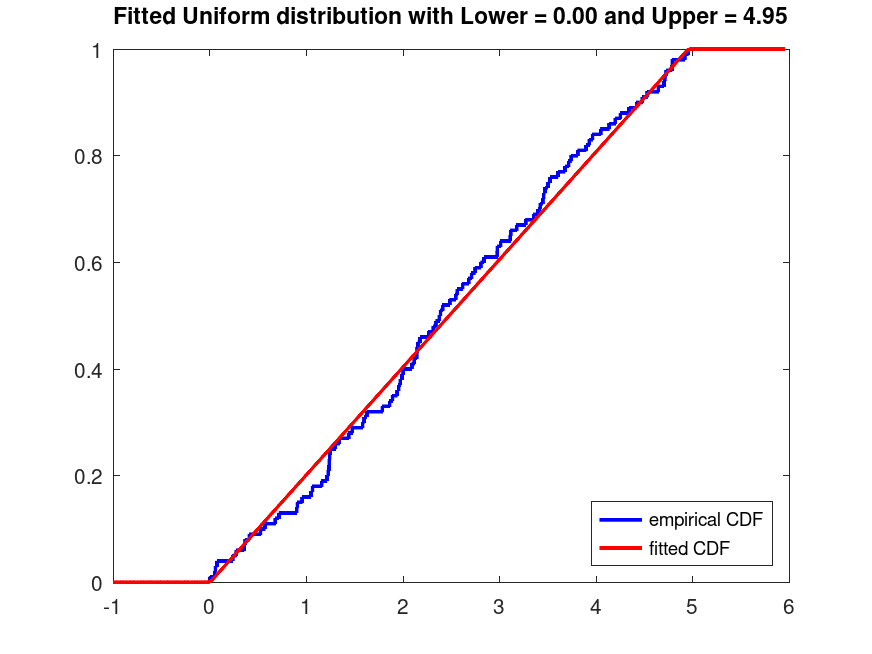
Example: 2


 ## Generate a data set of 100 random samples from a Uniform distribution
 ## with parameters Lower = 0 and Upper = 5. Fit a Uniform distribution to this
 ## data and plot its CDF superimposed over an empirical CDF.
 rand ("seed", 21);
 pd_fixed = makedist ("Uniform", "Lower", 0, "Upper", 5);
 data = random (pd_fixed, 100, 1);

 lower_hat = min (data);
 upper_hat = max (data);

 [f_empirical, x_empirical] = ecdf (data);
 stairs (x_empirical, f_empirical, 'b', 'LineWidth', 2);
 hold on;

 x = linspace (lower_hat - 1, upper_hat + 1, 200);
 y = (x - lower_hat) / (upper_hat - lower_hat);
 y(x < lower_hat) = 0;
 y(x > upper_hat) = 1;
 plot (x, y, 'r-', 'LineWidth', 2);

 % Title and legend
 txt = "Fitted Uniform distribution with Lower = %0.2f and Upper = %0.2f";
 title (sprintf (txt, lower_hat, upper_hat));
 legend ({"empirical CDF", "fitted CDF"}, "location", "southeast");
 hold off;

 ## Use this to visualize the fitted CDF compared to the empirical CDF of the
 ## data, useful for assessing model fit.

UniformDistribution: r = random (pd)
UniformDistribution: r = random (pd, rows)
UniformDistribution: r = random (pd, rows, cols, …)
UniformDistribution: r = random (pd, [sz])

r = random (pd) returns a random number from the distribution object pd.

When called with a single size argument, unifrnd returns a square matrix with the dimension specified. When called with more than one scalar argument, the first two arguments are taken as the number of rows and columns and any further arguments specify additional matrix dimensions. The size may also be specified with a row vector of dimensions, sz.

Example: 1


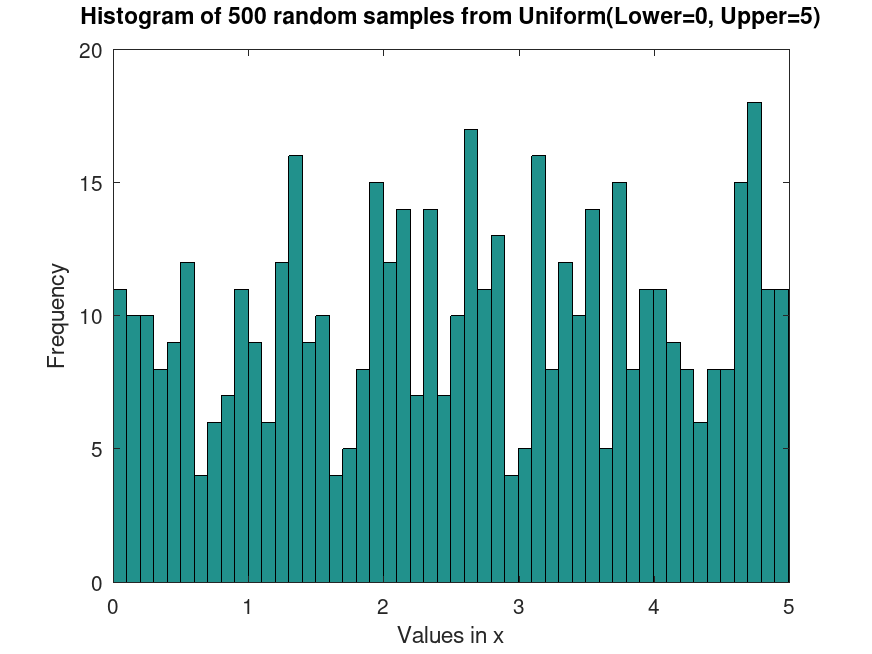
 ## Generate random samples from a Uniform distribution
 pd = makedist ("Uniform", "Lower", 0, "Upper", 5)
 rand ("seed", 21);
 samples = random (pd, 500, 1);
 hist (samples, 50)
 title ("Histogram of 500 random samples from Uniform(Lower=0, Upper=5)")
 xlabel ("Values in x")
 ylabel ("Frequency")

 ## This generates random samples from a Uniform distribution, useful
 ## for simulating data with equal probability over a fixed interval.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower = 0
    Upper = 5

UniformDistribution: s = std (pd)

s = std (pd) computes the standard deviation of the probability distribution object, pd.

Example: 1


 ## Compute the standard deviation for a Uniform distribution
 pd = makedist ("Uniform", "Lower", 0, "Upper", 10)
 std_value = std (pd)

 ## Use this to calculate the standard deviation, which measures the variability
 ## within the uniform interval.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower =  0
    Upper = 10

std_value = 2.8868

UniformDistribution: t = truncate (pd, lower, upper)

t = truncate (pd, lower, upper) returns a probability distribution t, which is the probability distribution pd truncated to the specified interval with lower limit, lower, and upper limit, upper. If pd is fitted to data with fitdist, the returned probability distribution t is not fitted, does not contain any data or estimated values, and it is as it has been created with the makedist function, but it includes the truncation interval.

Example: 1


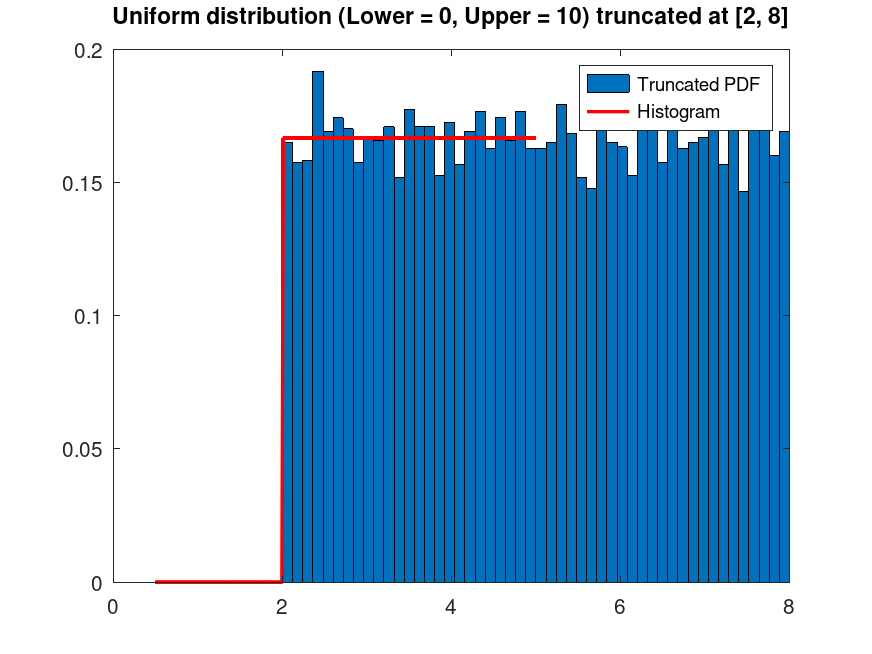
 ## Plot the PDF of a Uniform distribution, with parameters Lower = 0
 ## and Upper = 10, truncated at [2, 8] intervals. Generate 10000 random
 ## samples from this truncated distribution and superimpose a histogram scaled
 ## accordingly
 pd = makedist ("Uniform", "Lower", 0, "Upper", 10)
 t = truncate (pd, 2, 8)
 rand ("seed", 21);
 data = random (t, 10000, 1);

 [counts, centers] = hist (data, 50);
 bin_width = centers(2) - centers(1);
 bar (centers, counts / (sum (counts) * bin_width), 1);
 hold on;

 ## Plot histogram and truncated PDF
 x = linspace (0.5, 5, 500);
 y = pdf (t, x);
 plot (x, y, "r", "linewidth", 2);
 title ("Uniform distribution (Lower = 0, Upper = 10) truncated at [2, 8]")
 legend ("Truncated PDF", "Histogram")

 ## This demonstrates truncating a Uniform distribution to a specific
 ## range and visualizing the resulting distribution with random samples.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower =  0
    Upper = 10

t =
  UniformDistribution

  Uniform distribution (continuous)
    Lower =  0
    Upper = 10
  Truncated to the interval [2, 8]

UniformDistribution: v = var (pd)

v = var (pd) computes the variance of the probability distribution object, pd.

Example: 1


 ## Compute the variance for a Uniform distribution
 pd = makedist ("Uniform", "Lower", 0, "Upper", 10)
 var_value = var (pd)

 ## Use this to calculate the variance, which quantifies the spread of the
 ## values within the uniform interval.

pd =
  UniformDistribution

  Uniform distribution (continuous)
    Lower =  0
    Upper = 10

var_value = 8.3333

Examples

 pd = makedist ("Uniform", "Lower", 0, "Upper", 10);
 rand ("seed", 21);
 data = random (pd, 5000, 1);
 
 x = linspace (pd.Lower - 1, pd.Upper + 1, 500);
 y = pdf (pd, x);
 plot (x, y, 'r-', 'LineWidth', 2);
 hold on;
 
 [counts, centers] = hist (data, 50);
 bin_width = centers(2) - centers(1);
 normalized_counts = counts / (sum (counts) * bin_width);
 bar (centers, normalized_counts, 1);
 
 msg = "Uniform distribution with Lower = %0.2f and Upper = %0.2f";
 title (sprintf (msg, pd.Lower, pd.Upper));
 legend ("PDF", "Histogram", "location", "northeast");
 
 hold off;

Categories &

Functions List

Clustering

Clustering

Classification Classes

Classification Classes

Clustering Classes

Clustering Classes

Regression Classes

Regression Classes

Data Manipulation

Data Manipulation

Descriptive Statistics

Descriptive Statistics

Distribution Classes

Distribution Classes

Distribution Fitting

Distribution Fitting

Distribution Functions

Distribution Functions

Distribution Statistics

Distribution Statistics

Distribution Wrappers

Distribution Wrappers

Experimental Design

Experimental Design

Machine Learning

Machine Learning

Model Fitting

Model Fitting

Hypothesis Testing

Hypothesis Testing

I/O

I/O

Plotting

Plotting

Regression

Regression

Transforms

Transforms

Class Definition: UniformDistribution

statistics: UniformDistribution

Properties

Lower

Example: 1

Example: 2

Upper

Example: 1

Example: 2

DistributionName

NumParameters

ParameterNames

ParameterDescription

ParameterValues

Truncation

IsTruncated

Methods

cdf

UniformDistribution: p = cdf (pd, x)

UniformDistribution: p = cdf (pd, x, "upper")

Example: 1

icdf

UniformDistribution: x = icdf (pd, p)

Example: 1

iqr

UniformDistribution: r = iqr (pd)

Example: 1

mean

UniformDistribution: m = mean (pd)

Example: 1

median

UniformDistribution: m = median (pd)

Example: 1

pdf

UniformDistribution: y = pdf (pd, x)

Example: 1

plot

UniformDistribution: plot (pd)

UniformDistribution: plot (pd, Name, Value)

UniformDistribution: h = plot (…)

Class Definition: `UniformDistribution`

`Lower`

`Upper`

`DistributionName`

`NumParameters`

`ParameterNames`

`ParameterDescription`

`ParameterValues`

`Truncation`

`IsTruncated`

`cdf`

`UniformDistribution: p = cdf (pd, x)`

`UniformDistribution: p = cdf (pd, x, "upper")`

`icdf`

`UniformDistribution: x = icdf (pd, p)`

`iqr`

`UniformDistribution: r = iqr (pd)`

`mean`

`UniformDistribution: m = mean (pd)`

`median`

`UniformDistribution: m = median (pd)`

`pdf`

`UniformDistribution: y = pdf (pd, x)`

`plot`

`UniformDistribution: plot (pd)`

`UniformDistribution: plot (pd, Name, Value)`

`UniformDistribution: h = plot (…)`

`random`

`UniformDistribution: r = random (pd)`

`UniformDistribution: r = random (pd, rows)`

`UniformDistribution: r = random (pd, rows, cols, …)`

`UniformDistribution: r = random (pd, [sz])`

`std`

`UniformDistribution: s = std (pd)`

`truncate`

`UniformDistribution: t = truncate (pd, lower, upper)`

`var`

`UniformDistribution: v = var (pd)`