Categories &

Functions List

Function Reference: ricefit

statistics: paramhat = ricefit (x)
statistics: [paramhat, paramci] = ricefit (x)
statistics: [paramhat, paramci] = ricefit (x, alpha)
statistics: […] = ricefit (x, alpha, censor)
statistics: […] = ricefit (x, alpha, censor, freq)
statistics: […] = ricefit (x, alpha, censor, freq, options)

Estimate parameters and confidence intervals for the Gamma distribution.

paramhat = ricefit (x) returns the maximum likelihood estimates of the parameters of the Rician distribution given the data in x. paramhat(1) is the non-centrality (distance) parameter, s, and paramhat(2) is the scale parameter, sigma.

[paramhat, paramci] = ricefit (x) returns the 95% confidence intervals for the parameter estimates.

[…] = ricefit (x, alpha) also returns the 100 * (1 - alpha) percent confidence intervals for the parameter estimates. By default, the optional argument alpha is 0.05 corresponding to 95% confidence intervals. Pass in [] for alpha to use the default values.

[…] = ricefit (x, alpha, censor) accepts a boolean vector, censor, of the same size as x with 1s for observations that are right-censored and 0s for observations that are observed exactly. By default, or if left empty, censor = zeros (size (x)).

[…] = ricefit (x, alpha, censor, freq) accepts a frequency vector, freq, of the same size as x. freq typically contains integer frequencies for the corresponding elements in x, but it can contain any non-integer non-negative values. By default, or if left empty, freq = ones (size (x)).

[…] = ricefit (…, options) specifies control parameters for the iterative algorithm used to compute the maximum likelihood estimates. options is a structure with the following field and its default value:

  • options.Display = "off"
  • options.MaxFunEvals = 1000
  • options.MaxIter = 500
  • options.TolX = 1e-6

Further information about the Rician distribution can be found at https://en.wikipedia.org/wiki/Rice_distribution

See also: ricecdf, ricepdf, riceinv, ricernd, ricelike, ricestat

Source Code: ricefit

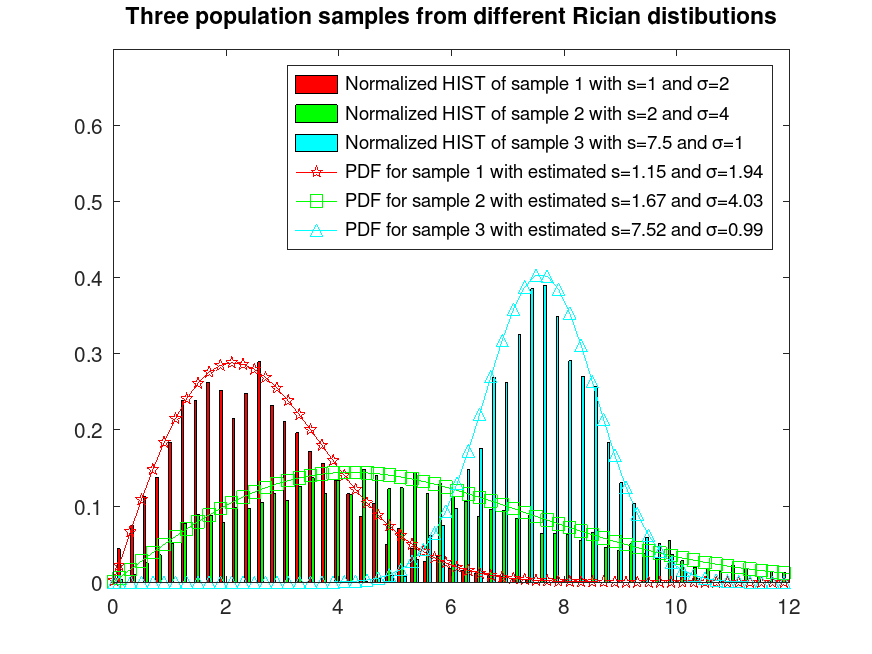
Example: 1

  

 ## Sample 3 populations from different Gamma distibutions
 randg ("seed", 5);    # for reproducibility
 randp ("seed", 6);
 r1 = ricernd (1, 2, 3000, 1);
 randg ("seed", 2);    # for reproducibility
 randp ("seed", 8);
 r2 = ricernd (2, 4, 3000, 1);
 randg ("seed", 7);    # for reproducibility
 randp ("seed", 9);
 r3 = ricernd (7.5, 1, 3000, 1);
 r = [r1, r2, r3];

 ## Plot them normalized and fix their colors
 hist (r, 75, 4);
 h = findobj (gca, "Type", "patch");
 set (h(1), "facecolor", "c");
 set (h(2), "facecolor", "g");
 set (h(3), "facecolor", "r");
 ylim ([0, 0.7]);
 xlim ([0, 12]);
 hold on

 ## Estimate their α and β parameters
 s_sigmaA = ricefit (r(:,1));
 s_sigmaB = ricefit (r(:,2));
 s_sigmaC = ricefit (r(:,3));

 ## Plot their estimated PDFs
 x = [0.01,0.1:0.2:18];
 y = ricepdf (x, s_sigmaA(1), s_sigmaA(2));
 plot (x, y, "-pr");
 y = ricepdf (x, s_sigmaB(1), s_sigmaB(2));
 plot (x, y, "-sg");
 y = ricepdf (x, s_sigmaC(1), s_sigmaC(2));
 plot (x, y, "-^c");
 hold off
 legend ({"Normalized HIST of sample 1 with s=1 and σ=2", ...
          "Normalized HIST of sample 2 with s=2 and σ=4", ...
          "Normalized HIST of sample 3 with s=7.5 and σ=1", ...
          sprintf("PDF for sample 1 with estimated s=%0.2f and σ=%0.2f", ...
                  s_sigmaA(1), s_sigmaA(2)), ...
          sprintf("PDF for sample 2 with estimated s=%0.2f and σ=%0.2f", ...
                  s_sigmaB(1), s_sigmaB(2)), ...
          sprintf("PDF for sample 3 with estimated s=%0.2f and σ=%0.2f", ...
                  s_sigmaC(1), s_sigmaC(2))})
 title ("Three population samples from different Rician distibutions")
 hold off
plotted figure