Categories &

Functions List

Function Reference: nbinfit

statistics: paramhat = nbinfit (x)
statistics: [paramhat, paramci] = nbinfit (x)
statistics: [paramhat, paramci] = nbinfit (x, alpha)
statistics: [paramhat, paramci] = nbinfit (x, alpha, freq)
statistics: [paramhat, paramci] = nbinfit (x, alpha, options)
statistics: [paramhat, paramci] = nbinfit (x, alpha, freq, options)

Estimate parameter and confidence intervals for the negative binomial distribution.

paramhat = nbinfit (x) returns the maximum likelihood estimates of the parameters of the negative binomial distribution given the data in vector x. paramhat(1) is the number of successes until the experiment is stopped, r, and paramhat(2) is the probability of success in each experiment, ps.

[paramhat, paramci] = nbinfit (x) returns the 95% confidence intervals for the parameter estimates.

[paramhat, paramci] = nbinfit (x, alpha) also returns the 100 * (1 - alpha) percent confidence intervals of the estimated parameter. By default, the optional argument alpha is 0.05 corresponding to 95% confidence intervals.

[…] = nbinlike (params, x, freq) accepts a frequency vector, freq, of the same size as x. freq must contain non-negative integer frequencies for the corresponding elements in x. By default, or if left empty, freq = ones (size (x)).

[paramhat, paramci] = nbinfit (x, alpha, options) specifies control parameters for the iterative algorithm used to compute ML estimates with the fminsearch function. options is a structure with the following fields and their default values:

  • options.Display = "off"
  • options.MaxFunEvals = 400
  • options.MaxIter = 200
  • options.TolX = 1e-6

When r is an integer, the negative binomial distribution is also known as the Pascal distribution and it models the number of failures in x before a specified number of successes is reached in a series of independent, identical trials. Its parameters are the probability of success in a single trial, ps, and the number of successes, r. A special case of the negative binomial distribution, when r = 1, is the geometric distribution, which models the number of failures before the first success.

r can also have non-integer positive values, in which form the negative binomial distribution, also known as the Polya distribution, has no interpretation in terms of repeated trials, but, like the Poisson distribution, it is useful in modeling count data. The negative binomial distribution is more general than the Poisson distribution because it has a variance that is greater than its mean, making it suitable for count data that do not meet the assumptions of the Poisson distribution. In the limit, as r increases to infinity, the negative binomial distribution approaches the Poisson distribution.

Further information about the negative binomial distribution can be found at https://en.wikipedia.org/wiki/Negative_binomial_distribution

See also: nbincdf, nbininv, nbinpdf, nbinrnd, nbinlike, nbinstat

Source Code: nbinfit

Example: 1

  

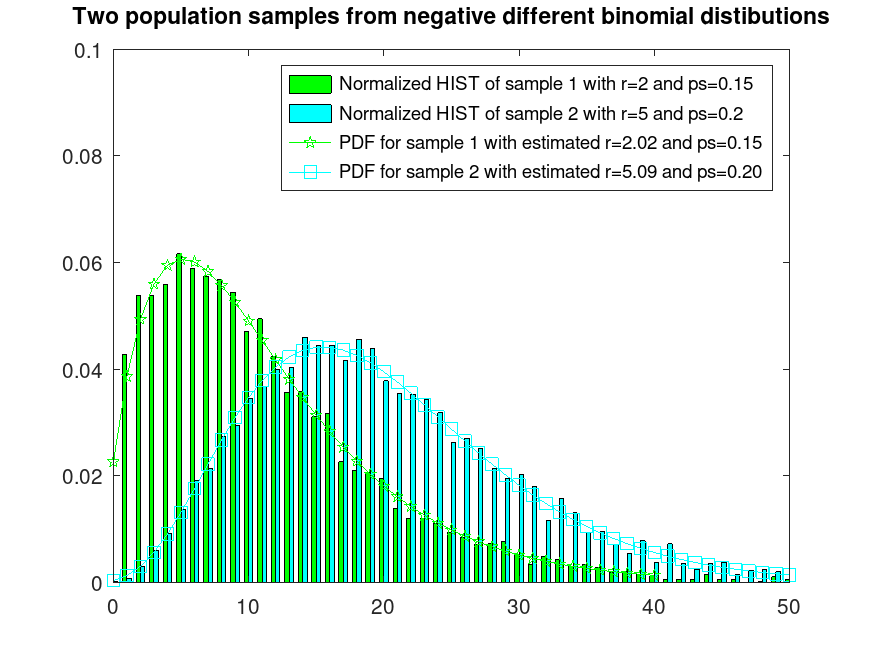
 ## Sample 2 populations from different negative binomial distibutions
 randp ("seed", 5); randg ("seed", 5);    # for reproducibility
 r1 = nbinrnd (2, 0.15, 5000, 1);
 randp ("seed", 8); randg ("seed", 8);    # for reproducibility
 r2 = nbinrnd (5, 0.2, 5000, 1);
 r = [r1, r2];

 ## Plot them normalized and fix their colors
 hist (r, [0:51], 1);
 h = findobj (gca, "Type", "patch");
 set (h(1), "facecolor", "c");
 set (h(2), "facecolor", "g");
 hold on

 ## Estimate their probability of success
 r_psA = nbinfit (r(:,1));
 r_psB = nbinfit (r(:,2));

 ## Plot their estimated PDFs
 x = [0:40];
 y = nbinpdf (x, r_psA(1), r_psA(2));
 plot (x, y, "-pg");
 x = [min(r(:,2)):max(r(:,2))];
 y = nbinpdf (x, r_psB(1), r_psB(2));
 plot (x, y, "-sc");
 ylim ([0, 0.1])
 xlim ([0, 50])
 legend ({"Normalized HIST of sample 1 with r=2 and ps=0.15", ...
          "Normalized HIST of sample 2 with r=5 and ps=0.2", ...
          sprintf("PDF for sample 1 with estimated r=%0.2f and ps=%0.2f", ...
                  r_psA(1), r_psA(2)), ...
          sprintf("PDF for sample 2 with estimated r=%0.2f and ps=%0.2f", ...
                  r_psB(1), r_psB(2))})
 title ("Two population samples from negative different binomial distibutions")
 hold off
plotted figure