Categories &

Functions List

Function Reference: evpdf

statistics: y = evpdf (x)
statistics: y = evpdf (x, mu)
statistics: y = evpdf (x, mu, sigma)

Extreme value probability density function (PDF).

For each element of x, compute the probability density function (PDF) of the extreme value distribution (also known as the Gumbel or the type I generalized extreme value distribution) with location parameter mu and scale parameter sigma. The size of y is the common size of x, mu and sigma. A scalar input functions as a constant matrix of the same size as the other inputs.

Default values are mu = 0 and sigma = 1.

The Gumbel distribution is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions. This version is suitable for modeling minima. For modeling maxima, use the alternative Gumbel iCDF, gumbelinv.

Further information about the Gumbel distribution can be found at https://en.wikipedia.org/wiki/Gumbel_distribution

See also: evcdf, evinv, evrnd, evfit, evlike, evstat, gumbelpdf

Source Code: evpdf

Example: 1

  

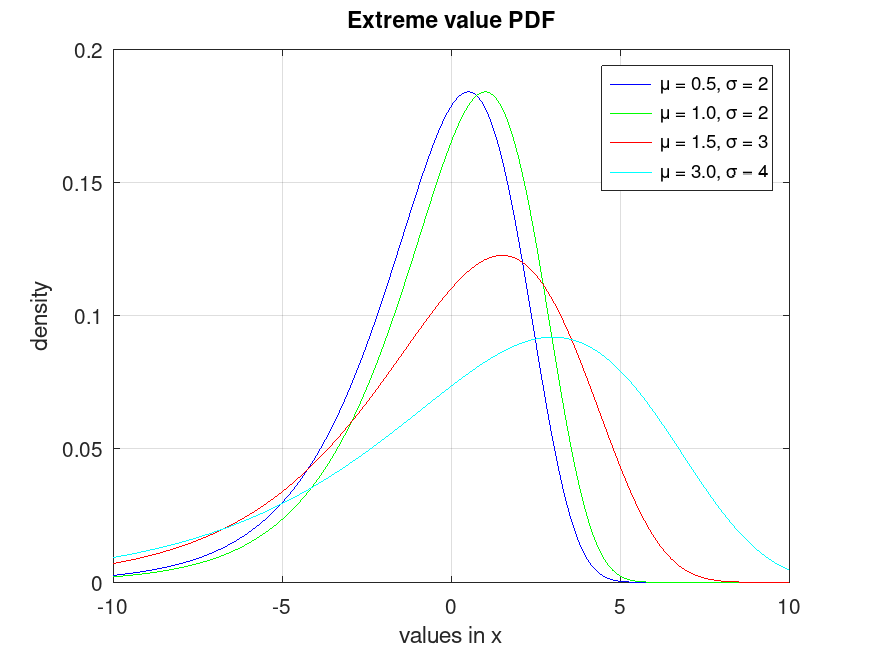
 ## Plot various PDFs from the Extreme value distribution
 x = -10:0.001:10;
 y1 = evpdf (x, 0.5, 2);
 y2 = evpdf (x, 1.0, 2);
 y3 = evpdf (x, 1.5, 3);
 y4 = evpdf (x, 3.0, 4);
 plot (x, y1, "-b", x, y2, "-g", x, y3, "-r", x, y4, "-c")
 grid on
 ylim ([0, 0.2])
 legend ({"μ = 0.5, σ = 2", "μ = 1.0, σ = 2", ...
          "μ = 1.5, σ = 3", "μ = 3.0, σ = 4"}, "location", "northeast")
 title ("Extreme value PDF")
 xlabel ("values in x")
 ylabel ("density")
plotted figure