Categories &

Functions List

Function Reference: procrustes

statistics: d = procrustes (X, Y)
statistics: d = procrustes (X, Y, param1, value1, …)
statistics: [d, Z] = procrustes (…)
statistics: [d, Z, transform] = procrustes (…)

Procrustes Analysis.

d = procrustes (X, Y) computes a linear transformation of the points in the matrix Y to best conform them to the points in the matrix X by minimizing the sum of squared errors, as the goodness of fit criterion, which is returned in d as a dissimilarity measure. d is standardized by a measure of the scale of X, given by

  • sum (sum ((X - repmat (mean (X, 1), size (X, 1), 1)) .^ 2, 1))

i.e., the sum of squared elements of a centered version of X. However, if X comprises repetitions of the same point, the sum of squared errors is not standardized.

X and Y must have the same number of points (rows) and procrustes matches the i-th point in Y to the i-th point in X. Points in Y can have smaller dimensions (columns) than those in X, but not the opposite. Missing dimensions in Y are added with padding columns of zeros as necessary to match the the dimensions in X.

[d, Z] = procrustes (X, Y) also returns the transformed values in Y.

[d, Z, transform] = procrustes (X, Y) also returns the transformation that maps Y to Z.

transform is a structure with fields:

cthe translation component
Tthe orthogonal rotation and reflection component
bthe scale component

So that Z = transform.b * Y * transform.T + transform.c

procrustes can take two optional parameters as Name-Value pairs.

[…] = procrustes (…, "Scaling", false) computes a transformation that does not include scaling, that is transform.b = 1. Setting "Scaling" to true includes a scaling component, which is the default.

[…] = procrustes (…, "Reflection", false) computes a transformation that does not include a reflection component, that is transform.T = 1. Setting "Reflection" to true forces the solution to include a reflection component in the computed transformation, that is transform.T = -1.

[…] = procrustes (…, "Reflection", "best") computes the best fit procrustes solution, which may or may not include a reflection component, which is the default.

See also: cmdscale

Source Code: procrustes

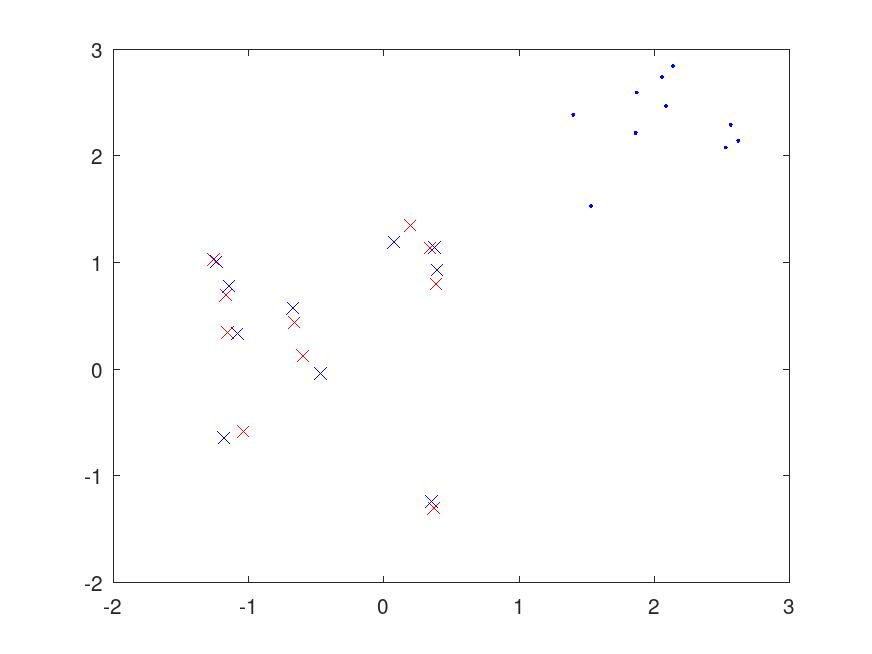
Example: 1

  

 ## Create some random points in two dimensions
 n = 10;
 randn ("seed", 1);
 X = normrnd (0, 1, [n, 2]);

 ## Those same points, rotated, scaled, translated, plus some noise
 S = [0.5, -sqrt(3)/2; sqrt(3)/2, 0.5]; # rotate 60 degrees
 Y = normrnd (0.5*X*S + 2, 0.05, n, 2);

 ## Conform Y to X, plot original X and Y, and transformed Y
 [d, Z] = procrustes (X, Y);
 plot (X(:,1), X(:,2), "rx", Y(:,1), Y(:,2), "b.", Z(:,1), Z(:,2), "bx");
plotted figure

Example: 2

  

 ## Find Procrustes distance and plot superimposed shape

 X = [40 88; 51 88; 35 78; 36 75; 39 72; 44 71; 48 71; 52 74; 55 77];
 Y = [36 43; 48 42; 31 26; 33 28; 37 30; 40 31; 45 30; 48 28; 51 24];
 plot (X(:,1),X(:,2),"x");
 hold on
 plot (Y(:,1),Y(:,2),"o");
 xlim ([0 100]);
 ylim ([0 100]);
 legend ("Target shape (X)", "Source shape (Y)");
 [d, Z] = procrustes (X, Y)
 plot (Z(:,1), Z(:,2), "s");
 legend ("Target shape (X)", "Source shape (Y)", "Transformed shape (Z)");
 hold off

d = 0.2026
Z =

   39.769   87.509
   50.562   86.801
   35.549   72.163
   37.313   73.991
   40.873   75.850
   43.552   76.796
   48.058   75.977
   50.783   74.229
   53.541   70.684
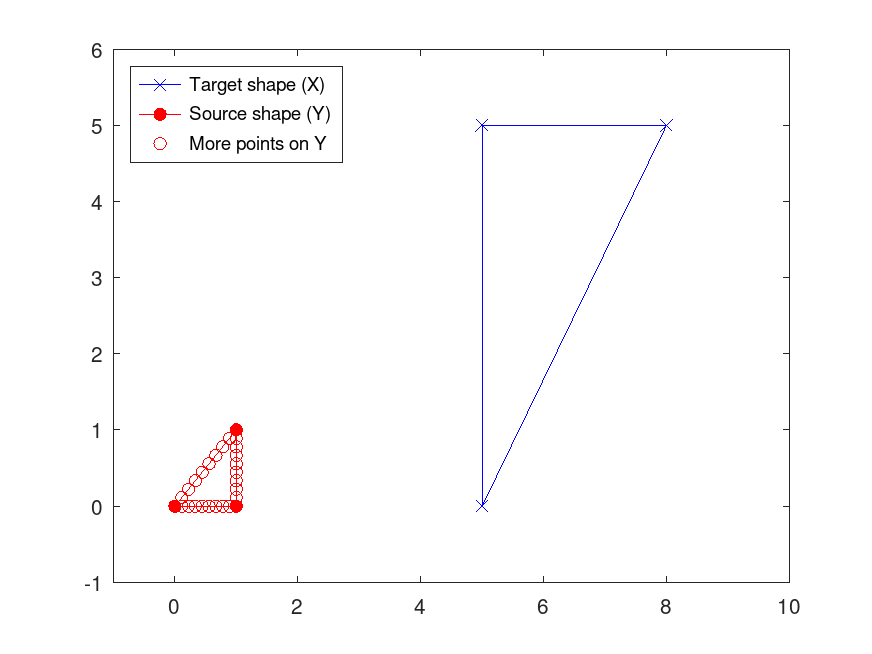
plotted figure

Example: 3

  

 ## Apply Procrustes transformation to larger set of points

 ## Create matrices with landmark points for two triangles
 X = [5, 0; 5, 5; 8, 5];   # target
 Y = [0, 0; 1, 0; 1, 1];   # source

 ## Create a matrix with more points on the source triangle
 Y_mp = [linspace(Y(1,1),Y(2,1),10)', linspace(Y(1,2),Y(2,2),10)'; ...
         linspace(Y(2,1),Y(3,1),10)', linspace(Y(2,2),Y(3,2),10)'; ...
         linspace(Y(3,1),Y(1,1),10)', linspace(Y(3,2),Y(1,2),10)'];

 ## Plot both shapes, including the larger set of points for the source shape
 plot ([X(:,1); X(1,1)], [X(:,2); X(1,2)], "bx-");
 hold on
 plot ([Y(:,1); Y(1,1)], [Y(:,2); Y(1,2)], "ro-", "MarkerFaceColor", "r");
 plot (Y_mp(:,1), Y_mp(:,2), "ro");
 xlim ([-1 10]);
 ylim ([-1 6]);
 legend ("Target shape (X)", "Source shape (Y)", ...
         "More points on Y", "Location", "northwest");
 hold off

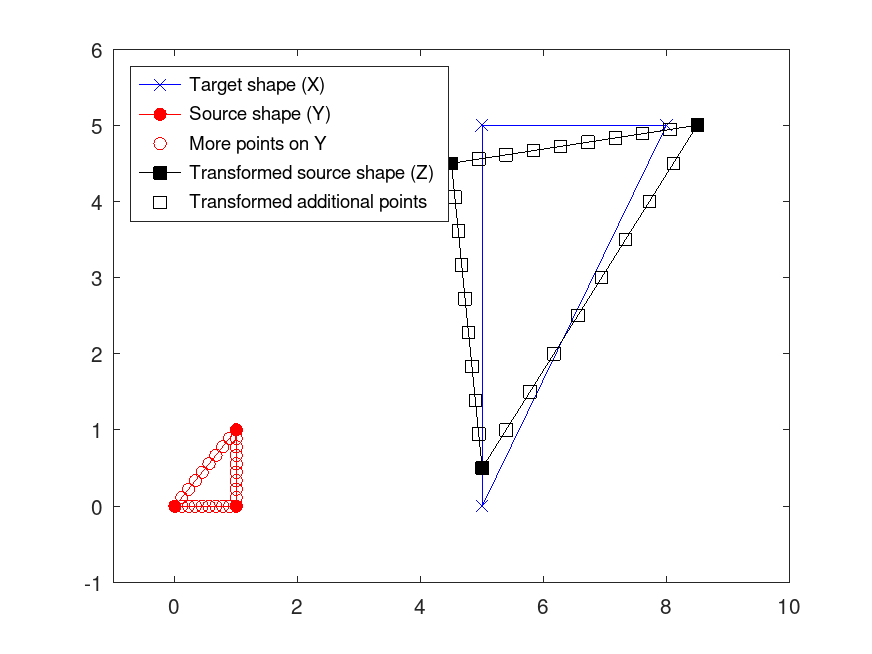
 ## Obtain the Procrustes transformation
 [d, Z, transform] = procrustes (X, Y)

 ## Use the Procrustes transformation to superimpose the more points (Y_mp)
 ## on the source shape onto the target shape, and then visualize the results.
 Z_mp = transform.b * Y_mp * transform.T + transform.c(1,:);
 figure
 plot ([X(:,1); X(1,1)], [X(:,2); X(1,2)], "bx-");
 hold on
 plot ([Y(:,1); Y(1,1)], [Y(:,2); Y(1,2)], "ro-", "MarkerFaceColor", "r");
 plot (Y_mp(:,1), Y_mp(:,2), "ro");
 xlim ([-1 10]);
 ylim ([-1 6]);
 plot ([Z(:,1); Z(1,1)],[Z(:,2); Z(1,2)],"ks-","MarkerFaceColor","k");
 plot (Z_mp(:,1),Z_mp(:,2),"ks");
 legend ("Target shape (X)", "Source shape (Y)", ...
         "More points on Y", "Transformed source shape (Z)", ...
         "Transformed additional points", "Location", "northwest");
 hold off

d = 0.044118
Z =

   5.0000   0.5000
   4.5000   4.5000
   8.5000   5.0000

transform =

  scalar structure containing the fields:

    T =

      -0.1240   0.9923
       0.9923   0.1240

    b = 4.0311
    c =

       5.0000   0.5000
       5.0000   0.5000
       5.0000   0.5000
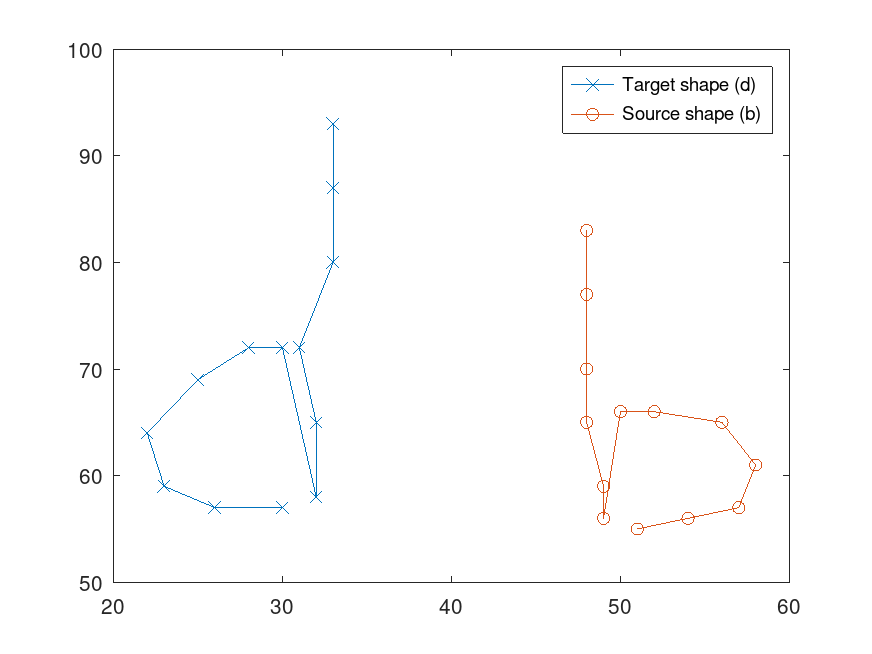
plotted figure

plotted figure

Example: 4

  

 ## Compare shapes without reflection

 T = [33, 93; 33, 87; 33, 80; 31, 72; 32, 65; 32, 58; 30, 72; ...
      28, 72; 25, 69; 22, 64; 23, 59; 26, 57; 30, 57];
 S = [48, 83; 48, 77; 48, 70; 48, 65; 49, 59; 49, 56; 50, 66; ...
      52, 66; 56, 65; 58, 61; 57, 57; 54, 56; 51, 55];
 plot (T(:,1), T(:,2), "x-");
 hold on
 plot (S(:,1), S(:,2), "o-");
 legend ("Target shape (d)", "Source shape (b)");
 hold off
 d_false = procrustes (T, S, "reflection", false);
 printf ("Procrustes distance without reflection: %f\n", d_false);
 d_true = procrustes (T, S, "reflection", true);
 printf ("Procrustes distance with reflection: %f\n", d_true);
 d_best = procrustes (T, S, "reflection", "best");
 printf ("Procrustes distance with best fit: %f\n", d_true);

Procrustes distance without reflection: 0.342463
Procrustes distance with reflection: 0.020428
Procrustes distance with best fit: 0.020428
plotted figure