Categories &
Functions List
- BetaDistribution
- BinomialDistribution
- BirnbaumSaundersDistribution
- BurrDistribution
- ExponentialDistribution
- ExtremeValueDistribution
- GammaDistribution
- GeneralizedExtremeValueDistribution
- GeneralizedParetoDistribution
- HalfNormalDistribution
- InverseGaussianDistribution
- LogisticDistribution
- LoglogisticDistribution
- LognormalDistribution
- LoguniformDistribution
- MultinomialDistribution
- NakagamiDistribution
- NegativeBinomialDistribution
- NormalDistribution
- PiecewiseLinearDistribution
- PoissonDistribution
- RayleighDistribution
- RicianDistribution
- tLocationScaleDistribution
- TriangularDistribution
- UniformDistribution
- WeibullDistribution
- betafit
- betalike
- binofit
- binolike
- bisafit
- bisalike
- burrfit
- burrlike
- evfit
- evlike
- expfit
- explike
- gamfit
- gamlike
- geofit
- gevfit_lmom
- gevfit
- gevlike
- gpfit
- gplike
- gumbelfit
- gumbellike
- hnfit
- hnlike
- invgfit
- invglike
- logifit
- logilike
- loglfit
- logllike
- lognfit
- lognlike
- nakafit
- nakalike
- nbinfit
- nbinlike
- normfit
- normlike
- poissfit
- poisslike
- raylfit
- rayllike
- ricefit
- ricelike
- tlsfit
- tlslike
- unidfit
- unifit
- wblfit
- wbllike
- betacdf
- betainv
- betapdf
- betarnd
- binocdf
- binoinv
- binopdf
- binornd
- bisacdf
- bisainv
- bisapdf
- bisarnd
- burrcdf
- burrinv
- burrpdf
- burrrnd
- bvncdf
- bvtcdf
- cauchycdf
- cauchyinv
- cauchypdf
- cauchyrnd
- chi2cdf
- chi2inv
- chi2pdf
- chi2rnd
- copulacdf
- copulapdf
- copularnd
- evcdf
- evinv
- evpdf
- evrnd
- expcdf
- expinv
- exppdf
- exprnd
- fcdf
- finv
- fpdf
- frnd
- gamcdf
- gaminv
- gampdf
- gamrnd
- geocdf
- geoinv
- geopdf
- geornd
- gevcdf
- gevinv
- gevpdf
- gevrnd
- gpcdf
- gpinv
- gppdf
- gprnd
- gumbelcdf
- gumbelinv
- gumbelpdf
- gumbelrnd
- hncdf
- hninv
- hnpdf
- hnrnd
- hygecdf
- hygeinv
- hygepdf
- hygernd
- invgcdf
- invginv
- invgpdf
- invgrnd
- iwishpdf
- iwishrnd
- jsucdf
- jsupdf
- laplacecdf
- laplaceinv
- laplacepdf
- laplacernd
- logicdf
- logiinv
- logipdf
- logirnd
- loglcdf
- loglinv
- loglpdf
- loglrnd
- logncdf
- logninv
- lognpdf
- lognrnd
- mnpdf
- mnrnd
- mvncdf
- mvnpdf
- mvnrnd
- mvtcdf
- mvtpdf
- mvtrnd
- mvtcdfqmc
- nakacdf
- nakainv
- nakapdf
- nakarnd
- nbincdf
- nbininv
- nbinpdf
- nbinrnd
- ncfcdf
- ncfinv
- ncfpdf
- ncfrnd
- nctcdf
- nctinv
- nctpdf
- nctrnd
- ncx2cdf
- ncx2inv
- ncx2pdf
- ncx2rnd
- normcdf
- norminv
- normpdf
- normrnd
- plcdf
- plinv
- plpdf
- plrnd
- poisscdf
- poissinv
- poisspdf
- poissrnd
- raylcdf
- raylinv
- raylpdf
- raylrnd
- ricecdf
- riceinv
- ricepdf
- ricernd
- tcdf
- tinv
- tpdf
- trnd
- tlscdf
- tlsinv
- tlspdf
- tlsrnd
- tricdf
- triinv
- tripdf
- trirnd
- unidcdf
- unidinv
- unidpdf
- unidrnd
- unifcdf
- unifinv
- unifpdf
- unifrnd
- vmcdf
- vminv
- vmpdf
- vmrnd
- wblcdf
- wblinv
- wblpdf
- wblrnd
- wienrnd
- wishpdf
- wishrnd
- adtest
- anova1
- anova2
- anovan
- bartlett_test
- barttest
- binotest
- chi2gof
- chi2test
- correlation_test
- fishertest
- friedman
- hotelling_t2test
- hotelling_t2test2
- kruskalwallis
- kstest
- kstest2
- levene_test
- manova1
- mcnemar_test
- multcompare
- ranksum
- regression_ftest
- regression_ttest
- runstest
- sampsizepwr
- signrank
- signtest
- tiedrank
- ttest
- ttest2
- vartest
- vartest2
- vartestn
- ztest
- ztest2
Function Reference: evalclusters
statistics: eva = evalclusters (x, clust, criterion)
statistics: eva = evalclusters (…,
Name,Value)
Create a clustering evaluation object to find the optimal number of clusters.
evalclusters creates a clustering evaluation object to evaluate the
optimal number of clusters for data x, using criterion criterion.
The input data x is a matrix with n observations of p
variables.
The evaluation criterion criterion is one of the following:
-
CalinskiHarabasz
to create a CalinskiHarabaszEvaluation object.
DaviesBouldin to create a DaviesBouldinEvaluation object.
gap to create a GapEvaluation object.
silhouette to create a SilhouetteEvaluation object.
The clustering algorithm clust is one of the following:
-
kmeans
to cluster the data using kmeans with EmptyAction set to
singleton and Replicates set to 5.
linkage to cluster the data using clusterdata with linkage set to
Ward.
gmdistribution to cluster the data using fitgmdist with SharedCov set to
true and Replicates set to 5.
If the criterion is CalinskiHarabasz, DaviesBouldin, or
silhouette, clust can also be a function handle to a function
of the form c = clust(x, k), where x is the input data,
k the number of clusters to evaluate and c the clustering result.
The clustering result can be either an array of size n with k
different integer values, or a matrix of size n by k with a
likelihood value assigned to each one of the n observations for each
one of the k clusters. In the latter case, each observation is assigned
to the cluster with the higher value.
If the criterion is CalinskiHarabasz, DaviesBouldin, or
silhouette, clust can also be a matrix of size n by
k, where k is the number of proposed clustering solutions, so
that each column of clust is a clustering solution.
In addition to the obligatory x, clust and criterion inputs
there is a number of optional arguments, specified as pairs of Name
and Value options. The known Name arguments are:
-
KList
a vector of positive integer numbers, that is the cluster sizes to evaluate. This option is necessary, unless clust is a matrix of proposed clustering solutions.
Distance a distance metric as accepted by the chosen clust. It can be the
name of the distance metric as a string or a function handle. When
criterion is silhouette, it can be a vector as created by
function pdist. Valid distance metric strings are: sqEuclidean
(default), Euclidean, cityblock, cosine,
correlation, Hamming, Jaccard.
Only used by silhouette and gap evaluation.
ClusterPriors the prior probabilities of each cluster, which can be either empirical
(default), or equal. When empirical the silhouette value is
the average of the silhouette values of all points; when equal the
silhouette value is the average of the average silhouette value of each
cluster. Only used by silhouette evaluation.
B the number of reference datasets generated from the reference distribution.
Only used by gap evaluation.
ReferenceDistribution the reference distribution used to create the reference data. It can be
PCA (default) for a distribution based on the principal components of
X, or uniform for a uniform distribution based on the range of
the observed data. PCA is currently not implemented.
Only used by gap evaluation.
SearchMethod the method for selecting the optimal value with a gap evaluation. It
can be either globalMaxSE (default) for selecting the smallest number
of clusters which is inside the standard error of the maximum gap value, or
firstMaxSE for selecting the first number of clusters which is inside
the standard error of the following cluster number.
Only used by gap evaluation.
Output eva is a clustering evaluation object.
See also: CalinskiHarabaszEvaluation, DaviesBouldinEvaluation, GapEvaluation, SilhouetteEvaluation
Source Code: evalclusters
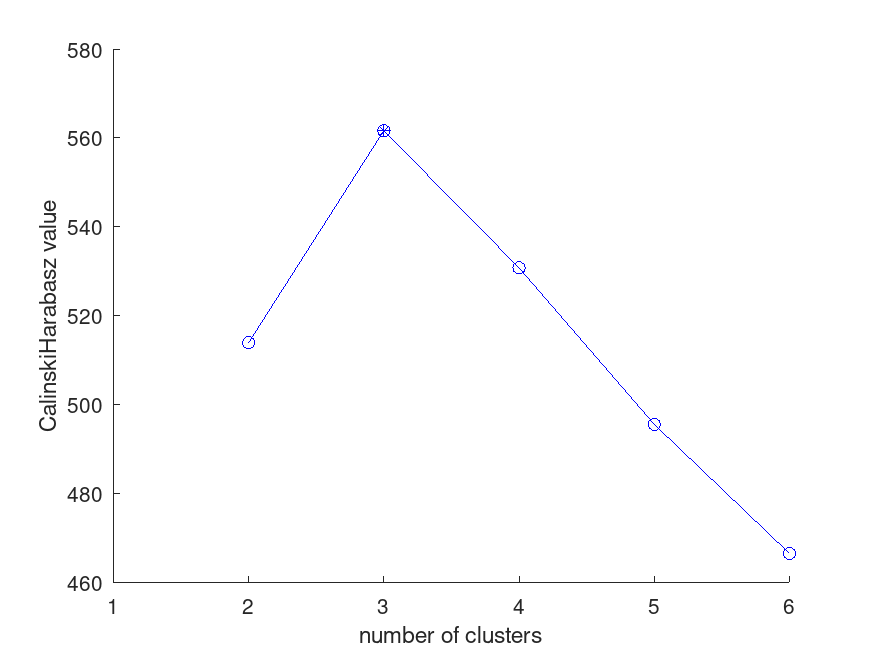
Example: 1
load fisheriris;
eva = evalclusters (meas, "kmeans", "calinskiharabasz", "KList", [1:6])
plot (eva)
eva =
CalinskiHarabaszEvaluation object with properties:
ClusteringFunction: 'kmeans'
CriterionName: "CalinskiHarabasz"
CriterionValues: [NaN, 513.92, 561.63, 530.39, 495.54, 473.85]
InspectedK: [1, 2, 3, 4, 5, 6]
Missing: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...]
NumObservations: 150
OptimalK: 3
OptimalY: [2; 2; 2; 2; 2; 2; 2; 2; 2; 2; ...]
X: [5.1000, 3.5000, 1.4000, 0.2000; 4.9000, 3, 1.4000, 0.2000; 4.7000, 3.2000, ...]
ans = -6.3303
|