Categories &

Functions List

Function Reference: invgfit

statistics: paramhat = invgfit (x)
statistics: [paramhat, paramci] = invgfit (x)
statistics: [paramhat, paramci] = invgfit (x, alpha)
statistics: […] = invgfit (x, alpha, censor)
statistics: […] = invgfit (x, alpha, censor, freq)
statistics: […] = invgfit (x, alpha, censor, freq, options)

Estimate mean and confidence intervals for the inverse Gaussian distribution.

mu0 = invgfit (x) returns the maximum likelihood estimates of the parameters of the inverse Gaussian distribution given the data in x. paramhat(1) is the scale parameter, mu, and paramhat(2) is the shape parameter, lambda.

[paramhat, paramci] = invgfit (x) returns the 95% confidence intervals for the parameter estimates.

[…] = invgfit (x, alpha) also returns the 100 * (1 - alpha) percent confidence intervals for the parameter estimates. By default, the optional argument alpha is 0.05 corresponding to 95% confidence intervals. Pass in [] for alpha to use the default values.

[…] = invgfit (x, alpha, censor) accepts a boolean vector, censor, of the same size as x with 1s for observations that are right-censored and 0s for observations that are observed exactly. By default, or if left empty, censor = zeros (size (x)).

[…] = invgfit (x, alpha, censor, freq) accepts a frequency vector, freq, of the same size as x. freq typically contains integer frequencies for the corresponding elements in x, but it can contain any non-integer non-negative values. By default, or if left empty, freq = ones (size (x)).

[…] = invgfit (…, options) specifies control parameters for the iterative algorithm used to compute ML estimates with the fminsearch function. options is a structure with the following fields and their default values:

  • options.Display = "off"
  • options.MaxFunEvals = 400
  • options.MaxIter = 200
  • options.TolX = 1e-6

Further information about the inverse Gaussian distribution can be found at https://en.wikipedia.org/wiki/Inverse_Gaussian_distribution

See also: invgcdf, invginv, invgpdf, invgrnd, invglike, invgstat

Source Code: invgfit

Example: 1

  

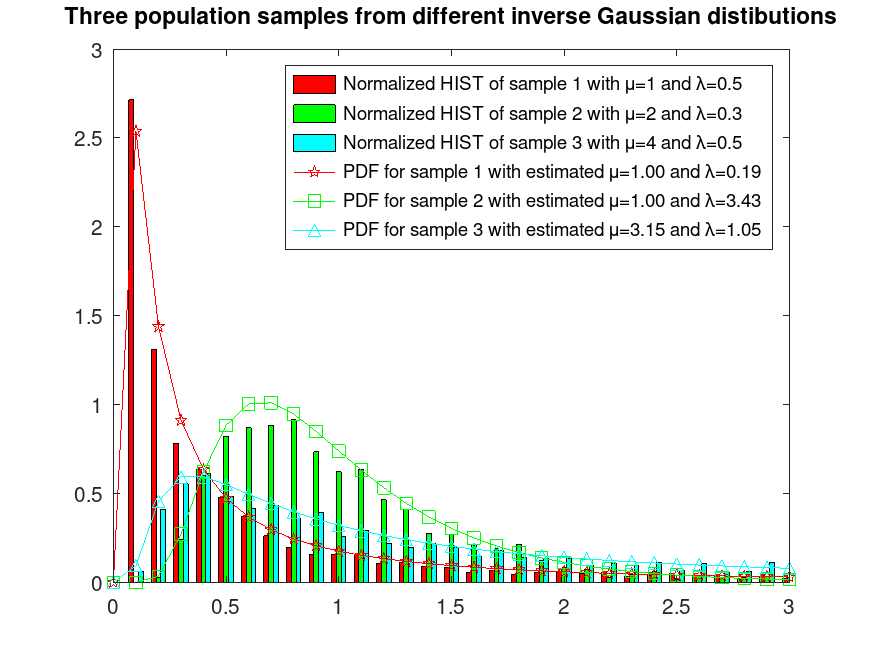
 ## Sample 3 populations from different inverse Gaussian distibutions
 rand ("seed", 5); randn ("seed", 5);   # for reproducibility
 r1 = invgrnd (1, 0.2, 2000, 1);
 rand ("seed", 2); randn ("seed", 2);   # for reproducibility
 r2 = invgrnd (1, 3, 2000, 1);
 rand ("seed", 7); randn ("seed", 7);   # for reproducibility
 r3 = invgrnd (3, 1, 2000, 1);
 r = [r1, r2, r3];

 ## Plot them normalized and fix their colors
 hist (r, [0.1:0.1:3.2], 9);
 h = findobj (gca, "Type", "patch");
 set (h(1), "facecolor", "c");
 set (h(2), "facecolor", "g");
 set (h(3), "facecolor", "r");
 ylim ([0, 3]);
 xlim ([0, 3]);
 hold on

 ## Estimate their MU and LAMBDA parameters
 mu_lambdaA = invgfit (r(:,1));
 mu_lambdaB = invgfit (r(:,2));
 mu_lambdaC = invgfit (r(:,3));

 ## Plot their estimated PDFs
 x = [0:0.1:3];
 y = invgpdf (x, mu_lambdaA(1), mu_lambdaA(2));
 plot (x, y, "-pr");
 y = invgpdf (x, mu_lambdaB(1), mu_lambdaB(2));
 plot (x, y, "-sg");
 y = invgpdf (x, mu_lambdaC(1), mu_lambdaC(2));
 plot (x, y, "-^c");
 hold off
 legend ({"Normalized HIST of sample 1 with μ=1 and λ=0.5", ...
          "Normalized HIST of sample 2 with μ=2 and λ=0.3", ...
          "Normalized HIST of sample 3 with μ=4 and λ=0.5", ...
          sprintf("PDF for sample 1 with estimated μ=%0.2f and λ=%0.2f", ...
                  mu_lambdaA(1), mu_lambdaA(2)), ...
          sprintf("PDF for sample 2 with estimated μ=%0.2f and λ=%0.2f", ...
                  mu_lambdaB(1), mu_lambdaB(2)), ...
          sprintf("PDF for sample 3 with estimated μ=%0.2f and λ=%0.2f", ...
                  mu_lambdaC(1), mu_lambdaC(2))})
 title ("Three population samples from different inverse Gaussian distibutions")
 hold off
plotted figure