Categories &

Functions List

Function Reference: slicesample

statistics: [smpl, neval] = slicesample (start, nsamples, property, value, …)

Draws nsamples samples from a target stationary distribution pdf using slice sampling of Radford M. Neal.

Input:

  • start is a 1 by dim vector of the starting point of the Markov chain. Each column corresponds to a different dimension.
  • nsamples is the number of samples, the length of the Markov chain.

Next, several property-value pairs can or must be specified, they are:

(Required properties) One of:

  • "pdf": the value is a function handle of the target stationary distribution to be sampled. The function should accept different locations in each row and each column corresponds to a different dimension.

    or

  • logpdf: the value is a function handle of the log of the target stationary distribution to be sampled. The function should accept different locations in each row and each column corresponds to a different dimension.

The following input property/pair values may be needed depending on the desired outut:

  • "burnin" burnin the number of points to discard at the beginning, the default is 0.
  • "thin" thin omitts m-1 of every m points in the generated Markov chain. The default is 1.
  • "width" width the maximum Manhattan distance between two samples. The default is 10.

Outputs:

  • smpl is a nsamples by dim matrix of random values drawn from pdf where the rows are different random values, the columns correspond to the dimensions of pdf.
  • neval is the number of function evaluations per sample.

Example : Sampling from a normal distribution

 
 
 start = 1;
 nsamples = 1e3;
 pdf = @(x) exp (-.5 * x .^ 2) / (pi ^ .5 * 2 ^ .5);
 [smpl, accept] = slicesample (start, nsamples, "pdf", pdf, "thin", 4);
 histfit (smpl);

See also: rand, mhsample, randsample

Source Code: slicesample

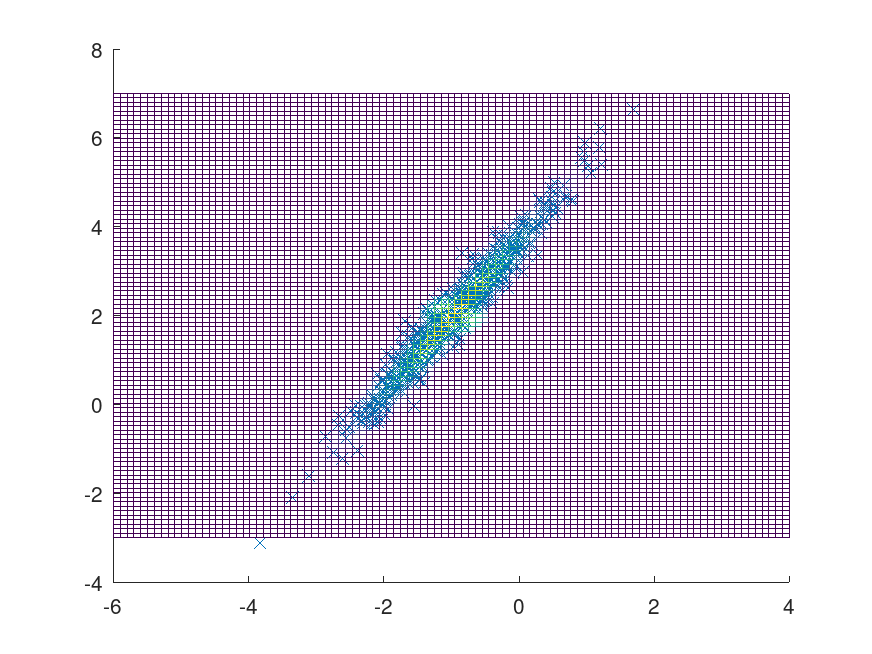
Example: 1

  

 ## Define function to sample
 d = 2;
 mu = [-1; 2];
 rand ("seed", 5)  # for reproducibility
 Sigma = rand (d);
 Sigma = (Sigma + Sigma');
 Sigma += eye (d)*abs (eigs (Sigma, 1, "sa")) * 1.1;
 pdf = @(x)(2*pi)^(-d/2)*det(Sigma)^-.5*exp(-.5*sum((x.'-mu).*(Sigma\(x.'-mu)),1));

 ## Inputs
 start = ones (1,2);
 nsamples = 500;
 K = 500;
 m = 10;
 rande ("seed", 4);  rand ("seed", 5)  # for reproducibility
 [smpl, accept] = slicesample (start, nsamples, "pdf", pdf, "burnin", K, "thin", m, "width", [20, 30]);
 figure;
 hold on;
 plot (smpl(:,1), smpl(:,2), 'x');
 [x, y] = meshgrid (linspace (-6,4), linspace(-3,7));
 z = reshape (pdf ([x(:), y(:)]), size(x));
 mesh (x, y, z, "facecolor", "None");

 ## Using sample points to find the volume of half a sphere with radius of .5
 f = @(x) ((.25-(x(:,1)+1).^2-(x(:,2)-2).^2).^.5.*(((x(:,1)+1).^2+(x(:,2)-2).^2)<.25)).';
 int = mean (f (smpl) ./ pdf (smpl));
 errest = std (f (smpl) ./ pdf (smpl)) / nsamples^.5;
 trueerr = abs (2/3*pi*.25^(3/2)-int);
 fprintf ("Monte Carlo integral estimate int f(x) dx = %f\n", int);
 fprintf ("Monte Carlo integral error estimate %f\n", errest);
 fprintf ("The actual error %f\n", trueerr);
 mesh (x,y,reshape (f([x(:), y(:)]), size(x)), "facecolor", "None");

Monte Carlo integral estimate int f(x) dx = 0.228408
Monte Carlo integral error estimate 0.029831
The actual error 0.033392
plotted figure

Example: 2

  

 ## Integrate truncated normal distribution to find normilization constant
 pdf = @(x) exp (-.5*x.^2)/(pi^.5*2^.5);
 nsamples = 1e3;
 rande ("seed", 4);  rand ("seed", 5)  # for reproducibility
 [smpl, accept] = slicesample (1, nsamples, "pdf", pdf, "thin", 4);
 f = @(x) exp (-.5 * x .^ 2) .* (x >= -2 & x <= 2);
 x = linspace (-3, 3, 1000);
 area (x, f(x));
 xlabel ("x");
 ylabel ("f(x)");
 int = mean (f (smpl) ./ pdf (smpl));
 errest = std (f (smpl) ./ pdf (smpl)) / nsamples ^ 0.5;
 trueerr = abs (erf (2 ^ 0.5) * 2 ^ 0.5 * pi ^ 0.5 - int);
 fprintf("Monte Carlo integral estimate int f(x) dx = %f\n", int);
 fprintf("Monte Carlo integral error estimate %f\n", errest);
 fprintf("The actual error %f\n", trueerr);

Monte Carlo integral estimate int f(x) dx = 2.376284
Monte Carlo integral error estimate 0.017608
The actual error 0.016292
plotted figure