Categories &

Functions List

Function Reference: vminv

statistics: x = vminv (p, mu, k)

Inverse of the von Mises cumulative distribution function (iCDF).

For each element of p, compute the quantile (the inverse of the CDF) of the von Mises distribution with location parameter mu and concentration parameter k on the interval [-pi,pi]. The size of x is the common size of p, mu, and k. A scalar input functions as a constant matrix of the same size as the other inputs.

Note: the quantile of the von Mises distribution is not analytic. Hence, it is approximated by a custom searching algorithm using its CDF until it converges up to a tolerance of 1e-5 or 100 iterations. As a result, balancing between performance and accuracy, the accuracy is about 5e-5 for k = 1 and it drops to 5e-5 as k increases.

Further information about the von Mises distribution can be found at https://en.wikipedia.org/wiki/Von_Mises_distribution

See also: vmcdf, vmpdf, vmrnd

Source Code: vminv

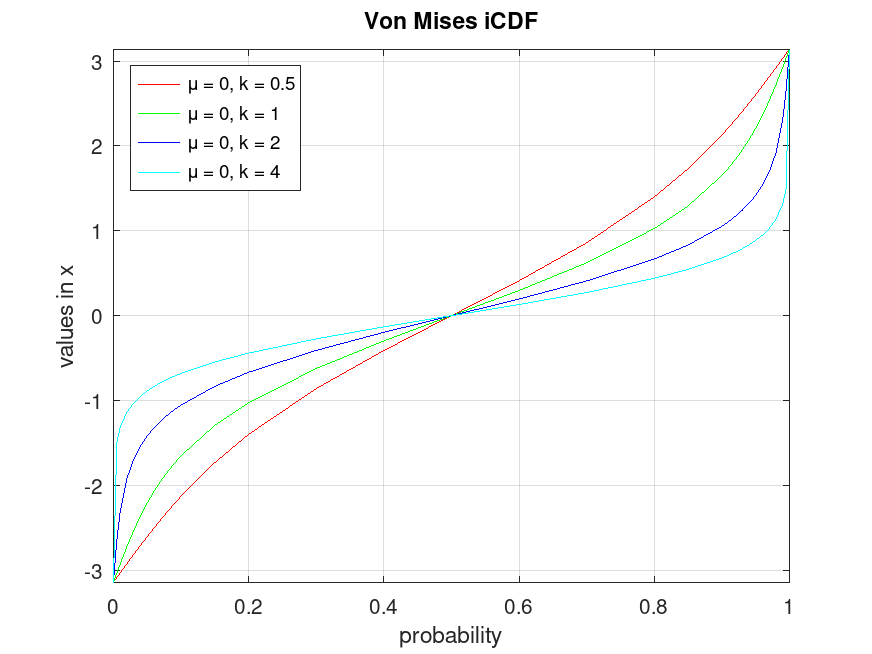
Example: 1

  

 ## Plot various iCDFs from the von Mises distribution
 p1 = [0,0.005,0.01:0.01:0.1,0.15,0.2:0.1:0.8,0.85,0.9:0.01:0.99,0.995,1];
 x1 = vminv (p1, 0, 0.5);
 x2 = vminv (p1, 0, 1);
 x3 = vminv (p1, 0, 2);
 x4 = vminv (p1, 0, 4);
 plot (p1, x1, "-r", p1, x2, "-g", p1, x3, "-b", p1, x4, "-c")
 grid on
 ylim ([-pi, pi])
 legend ({"μ = 0, k = 0.5", "μ = 0, k = 1", ...
          "μ = 0, k = 2", "μ = 0, k = 4"}, "location", "northwest")
 title ("Von Mises iCDF")
 xlabel ("probability")
 ylabel ("values in x")
plotted figure