Categories &

Functions List

Function Reference: vmpdf

statistics: y = vmpdf (x, mu, k)

Von Mises probability density function (PDF).

For each element of x, compute the probability density function (PDF) of the von Mises distribution with location parameter mu and concentration parameter k on the interval [-pi, pi]. The size of y is the common size of x, mu, and k. A scalar input functions as a constant matrix of the same size as the other inputs.

Further information about the von Mises distribution can be found at https://en.wikipedia.org/wiki/Von_Mises_distribution

See also: vmcdf, vminv, vmrnd

Source Code: vmpdf

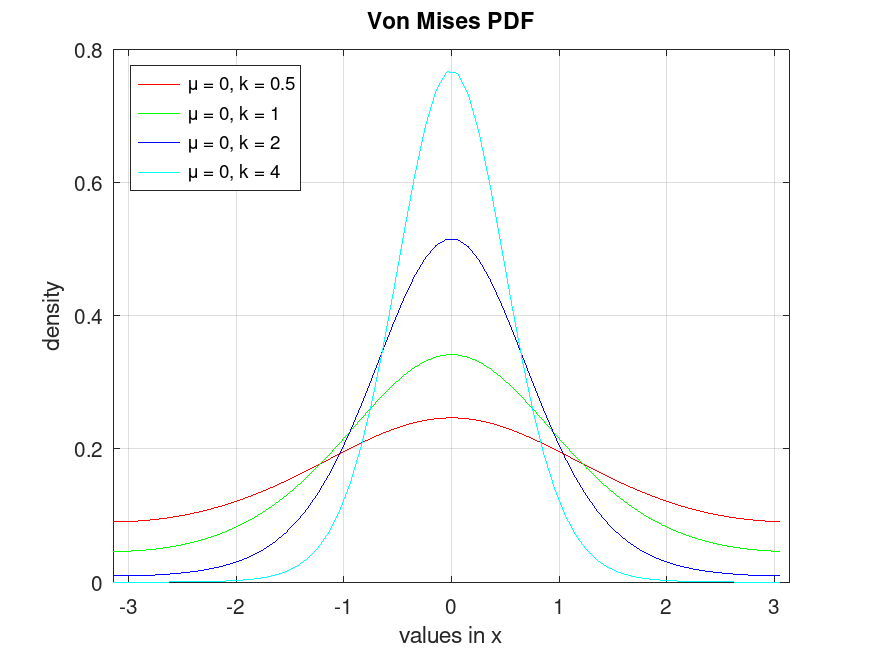
Example: 1

  

 ## Plot various PDFs from the von Mises distribution
 x1 = [-pi:0.1:pi];
 y1 = vmpdf (x1, 0, 0.5);
 y2 = vmpdf (x1, 0, 1);
 y3 = vmpdf (x1, 0, 2);
 y4 = vmpdf (x1, 0, 4);
 plot (x1, y1, "-r", x1, y2, "-g", x1, y3, "-b", x1, y4, "-c")
 grid on
 xlim ([-pi, pi])
 ylim ([0, 0.8])
 legend ({"μ = 0, k = 0.5", "μ = 0, k = 1", ...
          "μ = 0, k = 2", "μ = 0, k = 4"}, "location", "northwest")
 title ("Von Mises PDF")
 xlabel ("values in x")
 ylabel ("density")
plotted figure