Categories &

Functions List

Function Reference: fitcsvm

statistics: Mdl = fitcsvm (X, Y)
statistics: Mdl = fitcsvm (…, name, value)

Fit a Support Vector Machine classification model.

Mdl = fitcsvm (X, Y) returns a Support Vector Machine classification model, Mdl, with X being the predictor data, and Y the class labels of observations in X.

  • X must be a N×P numeric matrix of predictor data where rows correspond to observations and columns correspond to features or variables.
  • Y is N×1 matrix or cell matrix containing the class labels of corresponding predictor data in X. Y can be numerical, logical, char array or cell array of character vectors. Y must have same number of rows as X.

Mdl = fitcsvm (…, name, value) returns a Support Vector Machine model with additional options specified by Name-Value pair arguments listed below.

Model Parameters

NameValue
"Standardize"A boolean flag indicating whether the data in X should be standardized prior to training.
"PredictorNames"A cell array of character vectors specifying the predictor variable names. The variable names are assumed to be in the same order as they appear in the training data X.
"ResponseName"A character vector specifying the name of the response variable.
"ClassNames"Names of the classes in the class labels, Y, used for fitting the kNN model. ClassNames are of the same type as the class labels in Y.
"Prior"A numeric vector specifying the prior probabilities for each class. The order of the elements in Prior corresponds to the order of the classes in ClassNames.
"Cost"A N×R numeric matrix containing misclassification cost for the corresponding instances in X where R is the number of unique categories in Y. If an instance is correctly classified into its category the cost is calculated to be 1, otherwise 0. cost matrix can be altered use Mdl.cost = somecost. default value cost = ones(rows(X),numel(unique(Y))).
"SVMtype"Specifies the type of SVM used for training the ClassificationSVM model. By default, the type of SVM is defined by setting other parameters and/or by the data itself. Setting the "SVMtype" parameter overrides the default behavior and it accepts the following options:
ValueDescription
"C_SVC"It is the standard SVM formulation for classification tasks. It aims to find the optimal hyperplane that separates different classes by maximizing the margin between them while allowing some misclassifications. The parameter "C" controls the trade-off between maximizing the margin and minimizing the classification error. It is the default type, unless otherwise specified.
"nu_SVC"It is a variation of the standard SVM that introduces a parameter ν (nu) as an upper bound on the fraction of margin errors and a lower bound on the fraction of support vectors. This formulation provides more control over the number of support vectors and the margin errors, making it useful for specific classification scenarios. It is the default type, when the "OutlierFraction" parameter is set.
"one_class_SVM"It is used for anomaly detection and novelty detection tasks. It aims to separate the data points of a single class from the origin in a high-dimensional feature space. This method is particularly useful for identifying outliers or unusual patterns in the data. It is the default type, when the "Nu" parameter is set or when there is a single class in Y. When "one_class_SVM" is set by the "SVMtype" pair argument, Y has no effect and any classes are ignored.
NameValue
"OutlierFraction"The expected proportion of outliers in the training data, specified as a scalar value in the range [0,1]. When specified, the type of SVM model is switched to "nu_SVC" and "OutlierFraction" defines the ν (nu) parameter.
"KernelFunction"A character vector specifying the method for computing elements of the Gram matrix. The available kernel functions are 'gaussian' or 'rbf', 'linear', 'polynomial', and 'sigmoid'. For one-class learning, the default Kernel function is 'rbf'. For two-class learning the default is 'linear'.
"PolynomialOrder"A positive integer that specifies the order of polynomial in kernel function. The default value is 3. Unless the "KernelFunction" is set to 'polynomial', this parameter is ignored.
"KernelScale"A positive scalar that specifies a scaling factor for the γ (gamma) parameter, which can be seen as the inverse of the radius of influence of samples selected by the model as support vectors. The γ (gamma) parameter is computed as gamma = KernelScale / (number of features). The default value for "KernelScale" is 1.
"KernelOffset"A nonnegative scalar that specifies the coef0 in kernel function. For the polynomial kernel, it influences the polynomial’s shift, and for the sigmoid kernel, it affects the hyperbolic tangent’s shift. The default value for "KernelOffset" is 0.
"BoxConstraint"A positive scalar that specifies the upper bound of the Lagrange multipliers, i.e. the parameter C, which is used for training "C_SVC" and "one_class_SVM" type of models. It determines the trade-off between maximizing the margin and minimizing the classification error. The default value for "BoxConstraint" is 1.
"Nu"A positive scalar, in the range (0,1] that specifies the parameter ν (nu) for training "nu_SVC" and "one_class_SVM" type of models. Unless overriden by setting the "SVMtype" parameter, setting the "Nu" parameter always forces the training model type to "one_class_SVM", in which case, the number of classes in Y is ignored. The default value for "Nu" is 1.
"CacheSize"A positive scalar that specifies the memory requirements (in MB) for storing the Gram matrix. The default is 1000.
"Tolerance"A nonnegative scalar that specifies the tolerance of termination criterion. The default value is 1e-6.
"Shrinking"Specifies whether to use shrinking heuristics. It accepts either 0 or 1. The default value is 1.

Cross Validation Options

NameValue
"Crossval"Cross-validation flag specified as 'on' or 'off'. If 'on' is specified, a 10-fold cross validation is performed and a ClassificationPartitionedModel is returned in Mdl. To override this cross-validation setting, use only one of the following Name-Value pair arguments.
"CVPartition"A cvpartition object that specifies the type of cross-validation and the indexing for the training and validation sets. A ClassificationPartitionedModel is returned in Mdl and the trained model is stored in the Trained property.
"Holdout"Fraction of the data used for holdout validation, specified as a scalar value in the range [0,1]. When specified, a randomly selected percentage is reserved as validation data and the remaining set is used for training. The trained model is stored in the Trained property of the ClassificationPartitionedModel returned in Mdl. "Holdout" partitioning attempts to ensure that each partition represents the classes proportionately.
"KFold"Number of folds to use in the cross-validated model, specified as a positive integer value greater than 1. When specified, then the data is randomly partitioned in k sets and for each set, the set is reserved as validation data while the remaining k-1 sets are used for training. The trained models are stored in the Trained property of the ClassificationPartitionedModel returned in Mdl. "KFold" partitioning attempts to ensure that each partition represents the classes proportionately.
"Leaveout"Leave-one-out cross-validation flag specified as 'on' or 'off'. If 'on' is specified, then for each of the n observations (where n is the number of observations, excluding missing observations, specified in the NumObservations property of the model), one observation is reserved as validation data while the remaining observations are used for training. The trained models are stored in the Trained property of the ClassificationPartitionedModel returned in Mdl.

See also: ClassificationSVM, ClassificationPartitionedModel, svmtrain, svmpredict

Source Code: fitcsvm

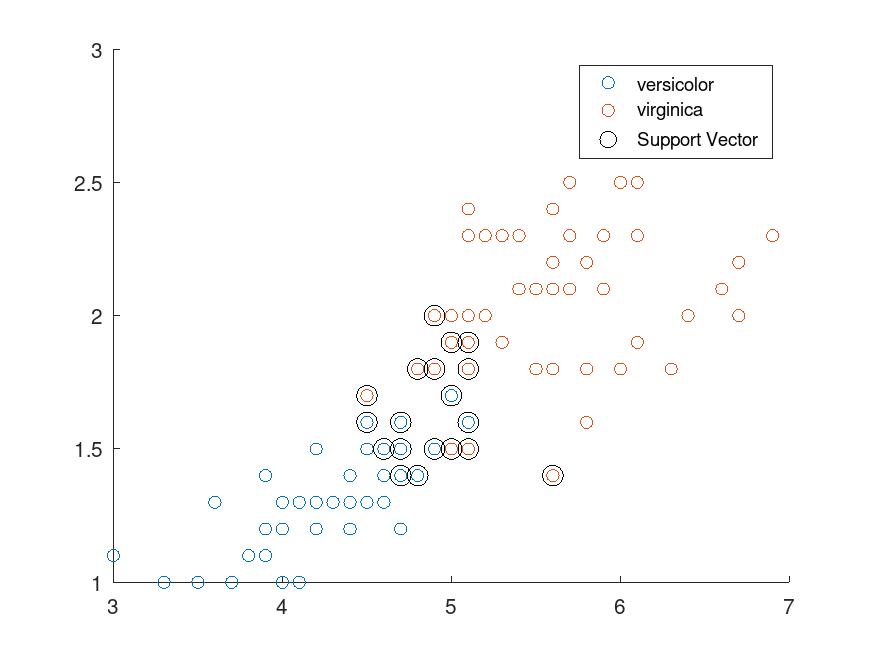
Example: 1

  

 ## Use a subset of Fisher's iris data set

 load fisheriris
 inds = ! strcmp (species, 'setosa');
 X = meas(inds, [3,4]);
 Y = species(inds);

 ## Train a linear SVM classifier
 SVMModel = fitcsvm (X, Y)

 ## Plot a scatter diagram of the data and circle the support vectors.
 sv = SVMModel.SupportVectors;
 figure
 gscatter (X(:,1), X(:,2), Y)
 hold on
 plot (sv(:,1), sv(:,2), 'ko', 'MarkerSize', 10)
 legend ('versicolor', 'virginica', 'Support Vector')
 hold off

SVMModel =

  ClassificationSVM object with properties:

                    Alpha: [24x1 double]
                     Beta: [0x0 double]
                     Bias: [1x1 double]
               ClassNames: [2x1 cell]
                     Cost: [2x2 double]
          IsSupportVector: [100x1 double]
                    Model: [1x1 struct]
          ModelParameters: [1x1 struct]
                       Mu: [0x0 double]
          NumObservations: [1x1 double]
            NumPredictors: [1x1 double]
           PredictorNames: [1x2 cell]
                    Prior: [2x1 double]
             ResponseName: Y
                 RowsUsed: [100x1 double]
           ScoreTransform: none
                    Sigma: [0x0 double]
              Standardize: 0
      SupportVectorLabels: [100x1 double]
           SupportVectors: [24x2 double]
                        X: [100x2 double]
                        Y: [100x1 cell]

ans =

  -179.36  -178.82
plotted figure