Categories &

Functions List

Function Reference: mvncdf

statistics: p = mvncdf (x)
statistics: p = mvncdf (x, mu, sigma)
statistics: p = mvncdf (x_lo, x_up, mu, sigma)
statistics: p = mvncdf (…, options)
statistics: [p, err] = mvncdf (…)

Multivariate normal cumulative distribution function (CDF).

p = mvncdf (x) returns the cumulative probability of the multivariate normal distribution evaluated at each row of x with zero mean and an identity covariance matrix. The rows of matrix x correspond to observations and its columns to variables. The return argument p is a column vector with the same number of rows as in x.

p = mvncdf (x, mu, sigma) returns cumulative probability of the multivariate normal distribution evaluated at each row of x with mean mu and a covariance matrix sigma. mu can be either a scalar (the same of every variable) or a row vector with the same number of elements as the number of variables in x. sigma covariance matrix may be specified a row vector if it only contains variances along its diagonal and zero covariances of the diagonal. In such a case, the diagonal vector sigma must have the same number of elements as the number of variables (columns) in x. If you only want to specify sigma, you can pass an empty matrix for mu.

The multivariate normal cumulative probability at x is defined as the probability that a random vector V, distributed as multivariate normal, will fall within the semi-infinite rectangle with upper limits defined by x.

  • PrV(1)<=X(1), V(2)<=X(2), ... V(D)<=X(D).

p = mvncdf (x_lo, x_hi, mu, sigma) returns the multivariate normal cumulative probability evaluated over the rectangle (hyper-rectangle for multivariate data in x) with lower and upper limits defined by x_lo and x_hi, respectively.

[p, err] = mvncdf (…) also returns an error estimate err in p.

p = mvncdf (…, options) specifies the structure, which controls specific parameters for the numerical integration used to compute p. The required fieds are:

"TolFun"Maximum absolute error tolerance. Default is 1e-8 for D < 4, or 1e-4 for D >= 4. Note that for bivariate normal cdf, the Octave implementation has a presicion of more than 1e-10.
"MaxFunEvals"Maximum number of integrand evaluations. Default is 1e7 for D > 4.
"Display"Display options. Choices are "off" (default), "iter", which shows the probability and estimated error at each repetition, and "final", which shows the final probability and related error after the integrand has converged successfully.

See also: bvncdf, mvnpdf, mvnrnd

Source Code: mvncdf

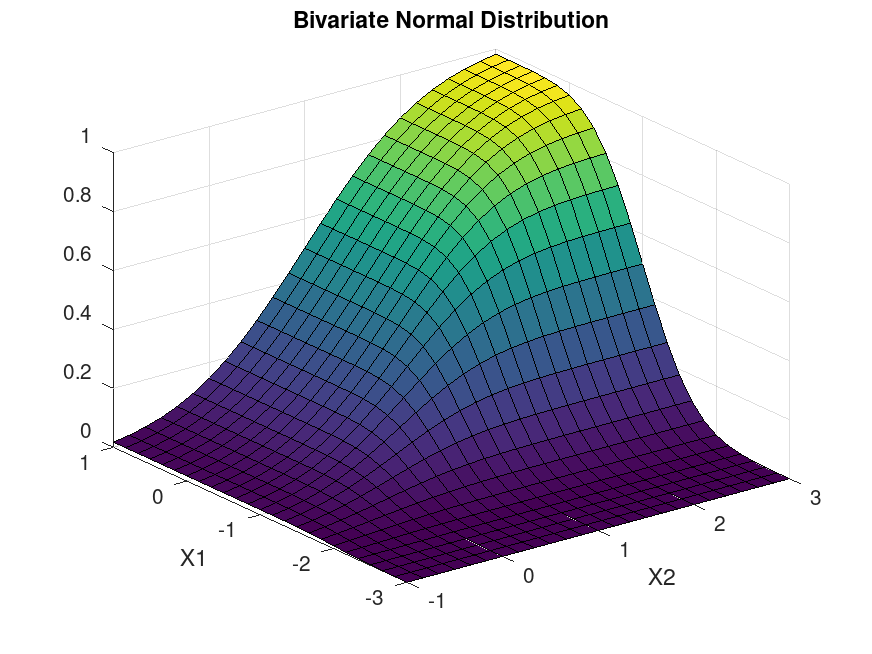
Example: 1

  

 mu = [1, -1];
 Sigma = [0.9, 0.4; 0.4, 0.3];
 [X1, X2] = meshgrid (linspace (-1, 3, 25)', linspace (-3, 1, 25)');
 X = [X1(:), X2(:)];
 p = mvncdf (X, mu, Sigma);
 Z = reshape (p, 25, 25);
 surf (X1, X2, Z);
 title ("Bivariate Normal Distribution");
 ylabel "X1"
 xlabel "X2"
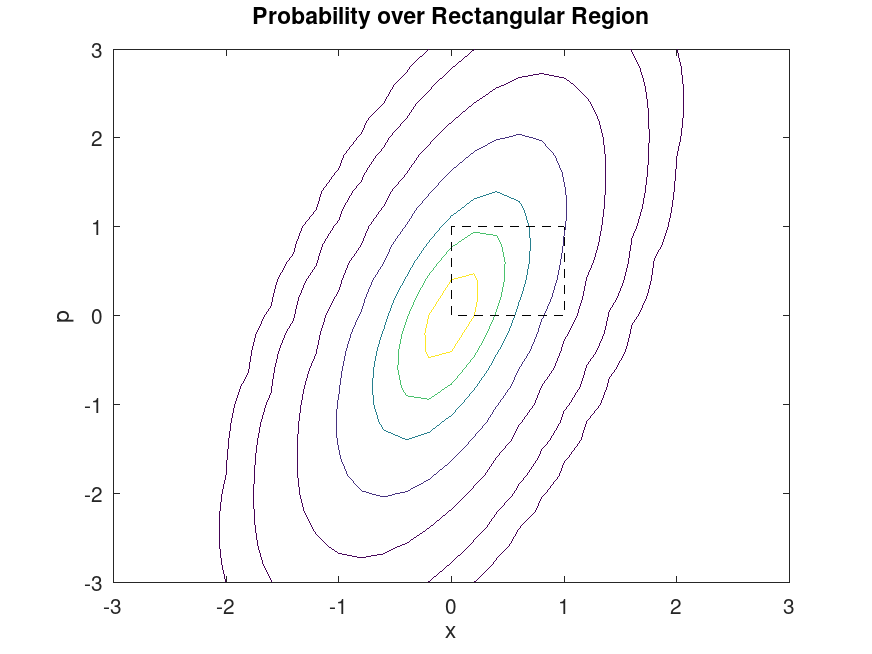
plotted figure

Example: 2

  

 mu = [0, 0];
 Sigma = [0.25, 0.3; 0.3, 1];
 p = mvncdf ([0 0], [1 1], mu, Sigma);
 x1 = -3:.2:3;
 x2 = -3:.2:3;
 [X1, X2] = meshgrid (x1, x2);
 X = [X1(:), X2(:)];
 p = mvnpdf (X, mu, Sigma);
 p = reshape (p, length (x2), length (x1));
 contour (x1, x2, p, [0.0001, 0.001, 0.01, 0.05, 0.15, 0.25, 0.35]);
 xlabel ("x");
 ylabel ("p");
 title ("Probability over Rectangular Region");
 line ([0, 0, 1, 1, 0], [1, 0, 0, 1, 1], "Linestyle", "--", "Color", "k");
plotted figure