Statistics: GeneralizedParetoDistribution

Class Definition: `GeneralizedParetoDistribution`

statistics: GeneralizedParetoDistribution

Generalized Pareto probability distribution object.

A GeneralizedParetoDistribution object consists of parameters, a model description, and sample data for a Generalized Pareto probability distribution.

The Generalized Pareto distribution is a continuous probability distribution that models the tail behavior of other distributions, commonly used for extreme value analysis. It is defined by shape parameter k, scale parameter sigma, and location parameter theta.

There are several ways to create a GeneralizedParetoDistribution object.

Fit a distribution to data using the fitdist function.
Create a distribution with fixed parameter values using the makedist function.
Use the constructor GeneralizedParetoDistribution (k, sigma, theta) to create a Generalized Pareto distribution with fixed parameter values k, sigma, and theta.
Use the static method GeneralizedParetoDistribution.fit (x, theta, alpha, freq, options) to fit a distribution to the data in x using the same input arguments as the gpfit function.

It is highly recommended to use fitdist and makedist functions to create probability distribution objects, instead of the class constructor or the aforementioned static method.

Further information about the Generalized Pareto distribution can be found at https://en.wikipedia.org/wiki/Generalized_Pareto_distribution

See also: fitdist, makedist, gpcdf, gpinv, gppdf, gprnd, gpfit, gplike, gpstat

Source Code: GeneralizedParetoDistribution

Properties

A scalar value characterizing the shape of the Generalized Pareto distribution. You can access the k property using dot name assignment.

Example: 1


 ## Create a Generalized Pareto distribution with default parameters
 pd = makedist ("GeneralizedPareto")

 ## Query parameter 'k' (shape parameter)
 pd.k

 ## Set parameter 'k'
 pd.k = 0.5

 ## Use this to initialize or modify the shape parameter of a Generalized Pareto
 ## distribution. The shape parameter can be any real scalar and determines the
 ## tail behavior (heavy-tailed if k>0).

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 1
    sigma = 1
    theta = 1

ans = 1
pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   1

Example: 2


 ## Create a Generalized Pareto distribution object by calling its constructor
 pd = GeneralizedParetoDistribution (0.5, 1, 0)

 ## Query parameter 'k'
 pd.k

 ## This demonstrates direct construction with a specific shape parameter,
 ## useful for modeling extreme values with known tail index.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

ans = 0.5000

A positive scalar value characterizing the scale of the Generalized Pareto distribution. You can access the sigma property using dot name assignment.

Example: 1


 ## Create a Generalized Pareto distribution with default parameters
 pd = makedist ("GeneralizedPareto")

 ## Query parameter 'sigma' (scale parameter)
 pd.sigma

 ## Set parameter 'sigma'
 pd.sigma = 2

 ## Use this to initialize or modify the scale parameter in a Generalized Pareto
 ## distribution. The scale parameter must be a positive real scalar.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 1
    sigma = 1
    theta = 1

ans = 1
pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 1
    sigma = 2
    theta = 1

Example: 2


 ## Create a Generalized Pareto distribution object by calling its constructor
 pd = GeneralizedParetoDistribution (0.5, 2, 0)

 ## Query parameter 'sigma'
 pd.sigma

 ## This shows how to set the scale parameter directly via the constructor,
 ## ideal for modeling the spread in extreme value data.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   2
    theta =   0

ans = 2

A scalar value characterizing the location of the Generalized Pareto distribution. You can access the theta property using dot name assignment.

Example: 1


 ## Create a Generalized Pareto distribution with default parameters
 pd = makedist ("GeneralizedPareto")

 ## Query parameter 'theta' (location parameter)
 pd.theta

 ## Set parameter 'theta'
 pd.theta = 1

 ## Use this to initialize or modify the location parameter in a Generalized Pareto
 ## distribution. The location parameter can be any real scalar, often set to a threshold in extreme value analysis.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 1
    sigma = 1
    theta = 1

ans = 1
pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 1
    sigma = 1
    theta = 1

Example: 2


 ## Create a Generalized Pareto distribution object by calling its constructor
 pd = GeneralizedParetoDistribution (0.5, 1, 1)

 ## Query parameter 'theta'
 pd.theta

 ## This demonstrates setting the location parameter directly, useful for shifting the distribution in threshold-exceedance models.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   1

ans = 1

A character vector specifying the name of the probability distribution object. This property is read-only.

A scalar integer value specifying the number of parameters characterizing the probability distribution. This property is read-only.

A $3×1$ cell array of character vectors with each element containing the name of a distribution parameter. This property is read-only.

A $3×1$ cell array of character vectors with each element containing a short description of a distribution parameter. This property is read-only.

A $3×1$ numeric vector containing the values of the distribution parameters. This property is read-only. You can change the distribution parameters by assigning new values to the k, sigma, and theta properties.

A $3×3$ numeric matrix containing the variance-covariance of the parameter estimates. Diagonal elements contain the variance of each estimated parameter, and non-diagonal elements contain the covariance between the parameter estimates. The covariance matrix is only meaningful when the distribution was fitted to data. If the distribution object was created with fixed parameters, or a parameter of a fitted distribution is modified, then all elements of the variance-covariance are zero. This property is read-only.

A $1×3$ logical vector specifying which parameters are fixed and which are estimated. true values correspond to fixed parameters, false values correspond to parameter estimates. This property is read-only.

A $1×2$ numeric vector specifying the truncation interval for the probability distribution. First element contains the lower boundary, second element contains the upper boundary. This property is read-only. You can only truncate a probability distribution with the truncate method.

A logical scalar value specifying whether a probability distribution is truncated or not. This property is read-only.

A scalar structure containing the following fields:

data: a numeric vector containing the data used for distribution fitting.
cens: a numeric vector of logical values indicating censoring information corresponding to the elements of the data used for distribution fitting. If no censoring vector was used for distribution fitting, then this field defaults to an empty array.
freq: a numeric vector of non-negative integer values containing the frequency information corresponding to the elements of the data used for distribution fitting. If no frequency vector was used for distribution fitting, then this field defaults to an empty array.

Methods

GeneralizedParetoDistribution: p = cdf (pd, x)
GeneralizedParetoDistribution: p = cdf (pd, x, "upper")

p = cdf (pd, x) computes the CDF of the probability distribution object, pd, evaluated at the values in x.

p = cdf (…, "upper") returns the complement of the CDF of the probability distribution object, pd, evaluated at the values in x.

Example: 1


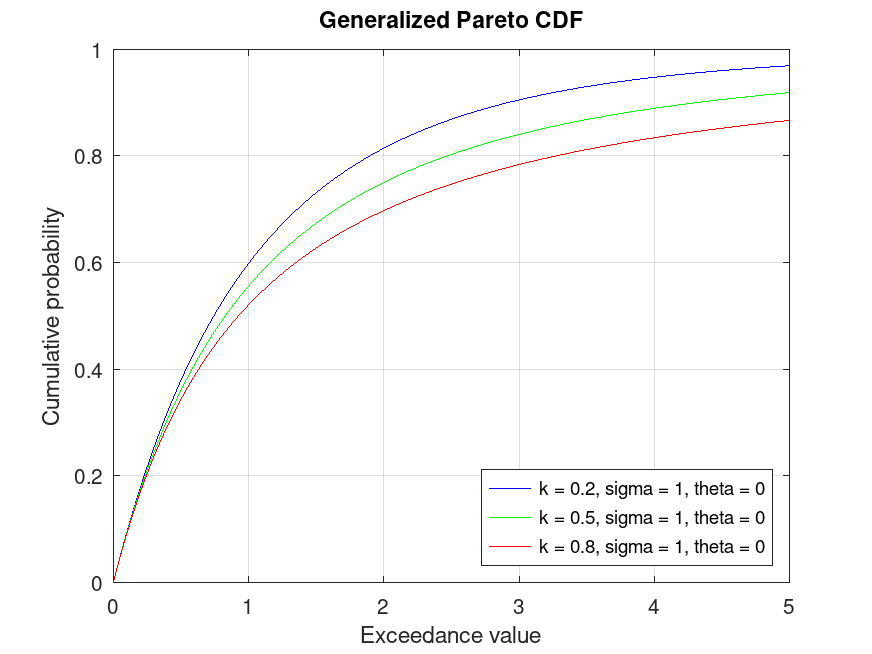
 ## Plot various CDFs from the Generalized Pareto distribution
 x = 0:0.01:5;
 pd1 = makedist ("GeneralizedPareto", "k", 0.2, "sigma", 1, "theta", 0);
 pd2 = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0);
 pd3 = makedist ("GeneralizedPareto", "k", 0.8, "sigma", 1, "theta", 0);
 p1 = cdf (pd1, x);
 p2 = cdf (pd2, x);
 p3 = cdf (pd3, x);
 plot (x, p1, "-b", x, p2, "-g", x, p3, "-r")
 grid on
 legend ({"k = 0.2, sigma = 1, theta = 0", "k = 0.5, sigma = 1, theta = 0", "k = 0.8, sigma = 1, theta = 0"}, ...
         "location", "southeast")
 title ("Generalized Pareto CDF")
 xlabel ("Exceedance value")
 ylabel ("Cumulative probability")

 ## Use this to compute and visualize the cumulative distribution function
 ## for different Generalized Pareto distributions, showing how probability
 ## accumulates over exceedance values in extreme value modeling.

GeneralizedParetoDistribution: x = icdf (pd, p)

x = icdf (pd, p) computes the quantile (the inverse of the CDF) of the probability distribution object, pd, evaluated at the values in p.

Example: 1


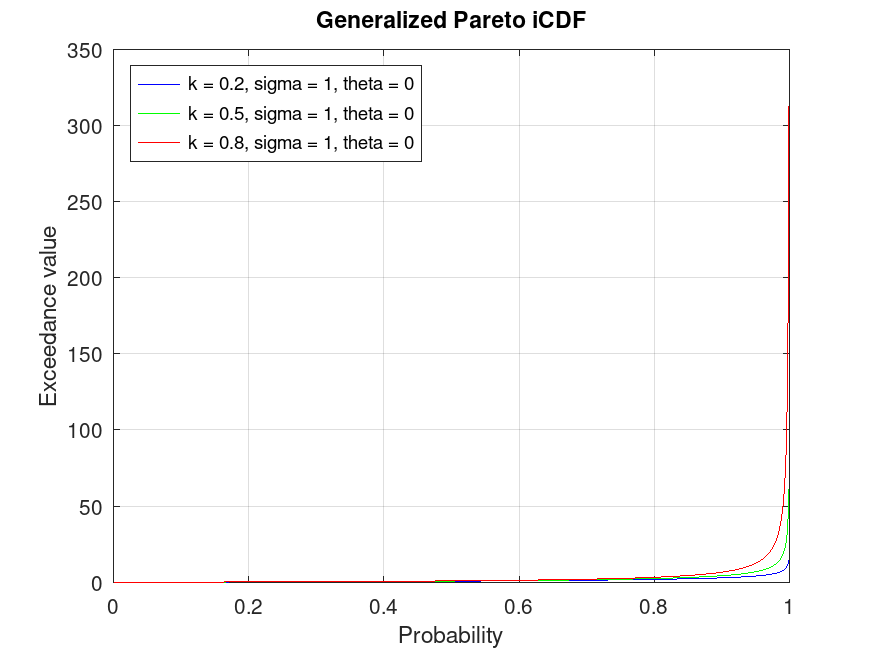
 ## Plot various iCDFs from the Generalized Pareto distribution
 p = 0.001:0.001:0.999;
 pd1 = makedist ("GeneralizedPareto", "k", 0.2, "sigma", 1, "theta", 0);
 pd2 = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0);
 pd3 = makedist ("GeneralizedPareto", "k", 0.8, "sigma", 1, "theta", 0);
 x1 = icdf (pd1, p);
 x2 = icdf (pd2, p);
 x3 = icdf (pd3, p);
 plot (p, x1, "-b", p, x2, "-g", p, x3, "-r")
 grid on
 legend ({"k = 0.2, sigma = 1, theta = 0", "k = 0.5, sigma = 1, theta = 0", "k = 0.8, sigma = 1, theta = 0"}, ...
         "location", "northwest")
 title ("Generalized Pareto iCDF")
 xlabel ("Probability")
 ylabel ("Exceedance value")

 ## This demonstrates the inverse CDF (quantiles) for Generalized Pareto
 ## distributions, useful for finding the exceedance value corresponding to
 ## given return probabilities in risk assessment.

GeneralizedParetoDistribution: r = iqr (pd)

r = iqr (pd) computes the interquartile range of the probability distribution object, pd.

Example: 1


 ## Compute the interquartile range for a Generalized Pareto distribution
 pd = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 iqr_value = iqr (pd)

 ## Use this to calculate the interquartile range, which measures the spread
 ## of the middle 50% of the distribution, useful for understanding variability
 ## in exceedance values.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

iqr_value = 1.6906

GeneralizedParetoDistribution: m = mean (pd)

m = mean (pd) computes the mean of the probability distribution object, pd.

Example: 1


 ## Compute the mean for different Generalized Pareto distributions
 pd1 = makedist ("GeneralizedPareto", "k", 0.2, "sigma", 1, "theta", 0);
 pd2 = makedist ("GeneralizedPareto", "k", 0.4, "sigma", 1, "theta", 0);
 mean1 = mean (pd1)
 mean2 = mean (pd2)

 ## This shows how to compute the expected exceedance value for Generalized Pareto
 ## distributions with different shape parameters (note: mean is finite only if k<1).

mean1 = 1.2500
mean2 = 1.6667

GeneralizedParetoDistribution: m = median (pd)

m = median (pd) computes the median of the probability distribution object, pd.

Example: 1


 ## Compute the median for different Generalized Pareto distributions
 pd1 = makedist ("GeneralizedPareto", "k", 0.2, "sigma", 1, "theta", 0);
 pd2 = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0);
 median1 = median (pd1)
 median2 = median (pd2)

 ## Use this to find the median exceedance value, which splits the distribution
 ## into two equal probability halves.

median1 = 0.7435
median2 = 0.8284

GeneralizedParetoDistribution: nlogL = negloglik (pd)

nlogL = negloglik (pd) computes the negative loglikelihood of the probability distribution object, pd.

Example: 1


 ## Compute the negative loglikelihood for a fitted Generalized Pareto distribution
 pd = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 rand ("seed", 21);
 data = random (pd, 100, 1);
 pd_fitted = GeneralizedParetoDistribution.fit (data, 0)
 nlogL = negloglik (pd_fitted)

 ## This is useful for assessing the fit of a Generalized Pareto distribution to
 ## data, lower values indicate a better fit.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

pd_fitted =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.605009   [0.327245, 0.882774]
    sigma = 0.958583   [0.697048, 1.31825]
    theta =        0

nlogL = -156.27

GeneralizedParetoDistribution: ci = paramci (pd)
GeneralizedParetoDistribution: ci = paramci (pd, Name, Value)

ci = paramci (pd) computes the lower and upper boundaries of the 95% confidence interval for each parameter of the probability distribution object, pd.

ci = paramci (pd, Name, Value) computes the confidence intervals with additional options specified by Name-Value pair arguments listed below.

`Name`		`Value`
`"Alpha"`		A scalar value in the range $(0,1)$ specifying the significance level for the confidence interval. The default value 0.05 corresponds to a 95% confidence interval.
`"Parameter"`		A character vector or a cell array of character vectors specifying the parameter names for which to compute confidence intervals. By default, `paramci` computes confidence intervals for all distribution parameters.

paramci is meaningful only when pd is fitted to data, otherwise an empty array, [], is returned.

Example: 1


 ## Compute confidence intervals for parameters of a fitted Generalized Pareto
 ## distribution
 pd = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 rand ("seed", 21);
 data = random (pd, 1000, 1);
 [phat, ci] = gpfit (data, 0, 0.05, []);
 disp ("Estimated parameters (k, sigma, theta):"), disp (phat)
 disp ("95% Confidence Intervals for k and sigma:"), disp (ci)

 ## Use this to obtain confidence intervals for the estimated parameters (k and sigma),
 ## providing a range of plausible values given the data (theta is fixed).

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

Estimated parameters (k, sigma, theta):
   0.5061   0.9545        0
95% Confidence Intervals for k and sigma:
   0.4156   0.8592        0
   0.5967   1.0603        0

GeneralizedParetoDistribution: y = pdf (pd, x)

y = pdf (pd, x) computes the PDF of the probability distribution object, pd, evaluated at the values in x.

Example: 1


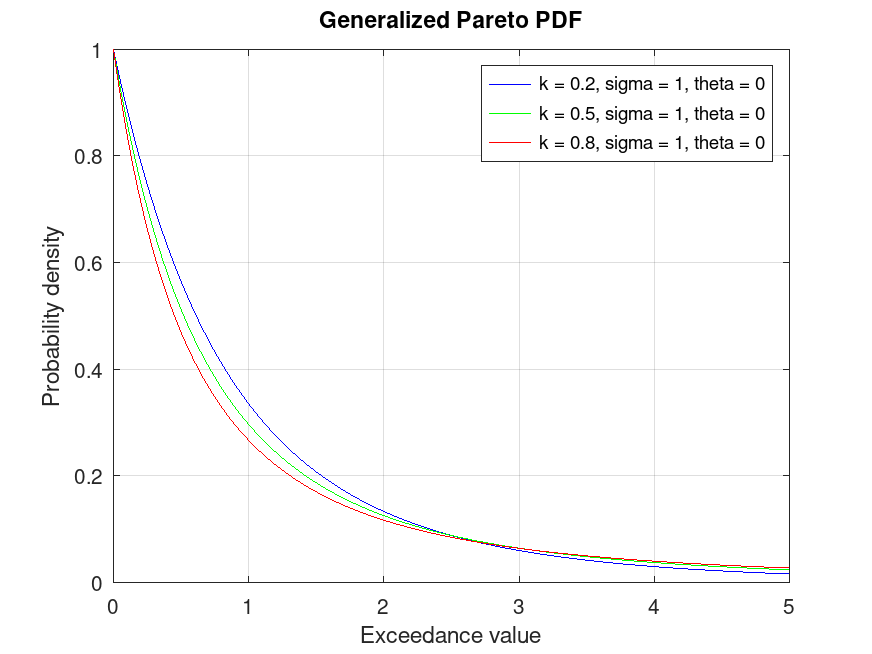
 ## Plot various PDFs from the Generalized Pareto distribution
 x = 0:0.01:5;
 pd1 = makedist ("GeneralizedPareto", "k", 0.2, "sigma", 1, "theta", 0);
 pd2 = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0);
 pd3 = makedist ("GeneralizedPareto", "k", 0.8, "sigma", 1, "theta", 0);
 y1 = pdf (pd1, x);
 y2 = pdf (pd2, x);
 y3 = pdf (pd3, x);
 plot (x, y1, "-b", x, y2, "-g", x, y3, "-r")
 grid on
 legend ({"k = 0.2, sigma = 1, theta = 0", "k = 0.5, sigma = 1, theta = 0", "k = 0.8, sigma = 1, theta = 0"}, ...
         "location", "northeast")
 title ("Generalized Pareto PDF")
 xlabel ("Exceedance value")
 ylabel ("Probability density")

 ## This visualizes the probability density function for Generalized Pareto
 ## distributions, showing the likelihood of different exceedance values.

GeneralizedParetoDistribution: plot (pd)
GeneralizedParetoDistribution: plot (pd, Name, Value)
GeneralizedParetoDistribution: h = plot (…)

plot (pd) plots a probability density function (PDF) of the probability distribution object pd. If pd contains data, which have been fitted by fitdist, the PDF is superimposed over a histogram of the data.

plot (pd, Name, Value) specifies additional options with the Name-Value pair arguments listed below.

`Name`		`Value`
`"PlotType"`		A character vector specifying the plot type. `"pdf"` plots the probability density function (PDF). When `pd` is fit to data, the PDF is superimposed on a histogram of the data. `"cdf"` plots the cumulative density function (CDF). When `pd` is fit to data, the CDF is superimposed over an empirical CDF. `"probability"` plots a probability plot using a CDF of the data and a CDF of the fitted probability distribution. This option is available only when `pd` is fitted to data.
`"Discrete"`		A logical scalar to specify whether to plot the PDF or CDF of a discrete distribution object as a line plot or a stem plot, by specifying `false` or `true`, respectively. By default, it is `true` for discrete distributions and `false` for continuous distributions. When `pd` is a continuous distribution object, option is ignored.
`"Parent"`		An axes graphics object for plot. If not specified, the `plot` function plots into the current axes or creates a new axes object if one does not exist.

h = plot (…) returns a graphics handle to the plotted objects.

Example: 1


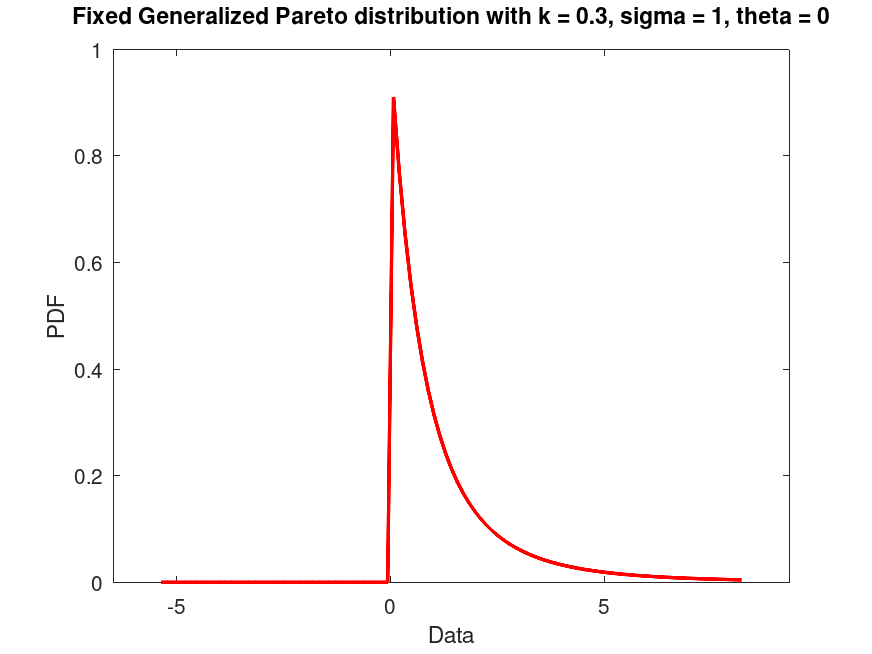
 ## Create a Generalized Pareto distribution with fixed parameters k = 0.5, sigma = 1, theta = 0
 ## and plot its PDF.

 pd = makedist ("GeneralizedPareto", "k", 0.3, "sigma", 1, "theta", 0)
 plot (pd)
 title ("Fixed Generalized Pareto distribution with k = 0.3, sigma = 1, theta = 0")

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.3
    sigma =   1
    theta =   0

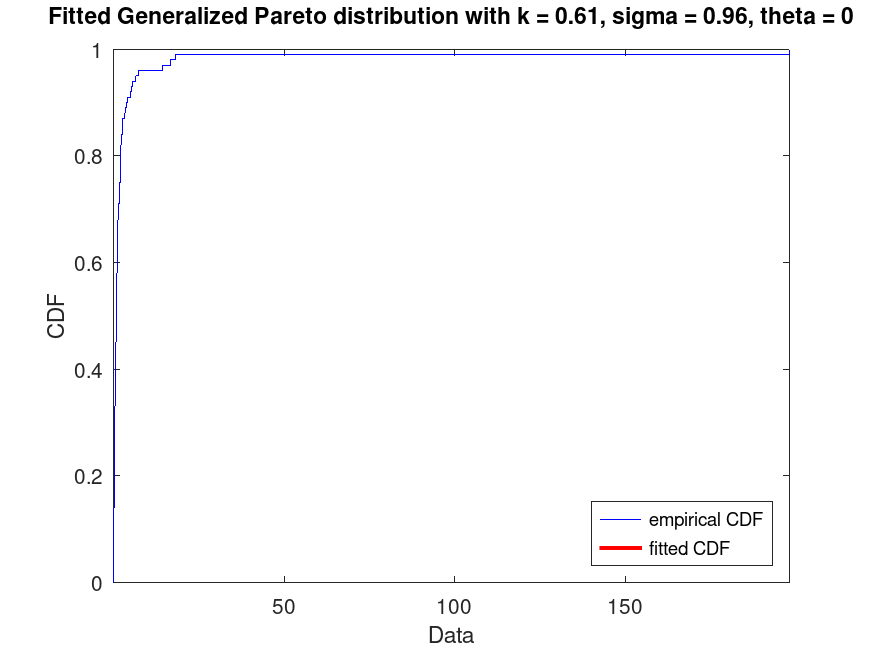
Example: 2


 ## Generate a data set of 100 random samples from a Generalized Pareto
 ## distribution with parameters k = 0.5, sigma = 1, theta = 0. Fit a Generalized Pareto
 ## distribution to this data (fixing theta=0) and plot its CDF superimposed over an empirical
 ## CDF.

 pd_fixed = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 rand ("seed", 21);
 data = random (pd_fixed, 100, 1);
 pd_fitted = GeneralizedParetoDistribution.fit (data, 0)
 plot (pd_fitted, "PlotType", "cdf")
 txt = "Fitted Generalized Pareto distribution with k = %0.2f, sigma = %0.2f, theta = 0";
 title (sprintf (txt, pd_fitted.k, pd_fitted.sigma))
 legend ({"empirical CDF", "fitted CDF"}, "location", "southeast")

 ## Use this to visualize the fitted CDF compared to the empirical CDF of the
 ## data, useful for assessing model fit in extreme value analysis.

pd_fixed =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

pd_fitted =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.605009   [0.327245, 0.882774]
    sigma = 0.958583   [0.697048, 1.31825]
    theta =        0

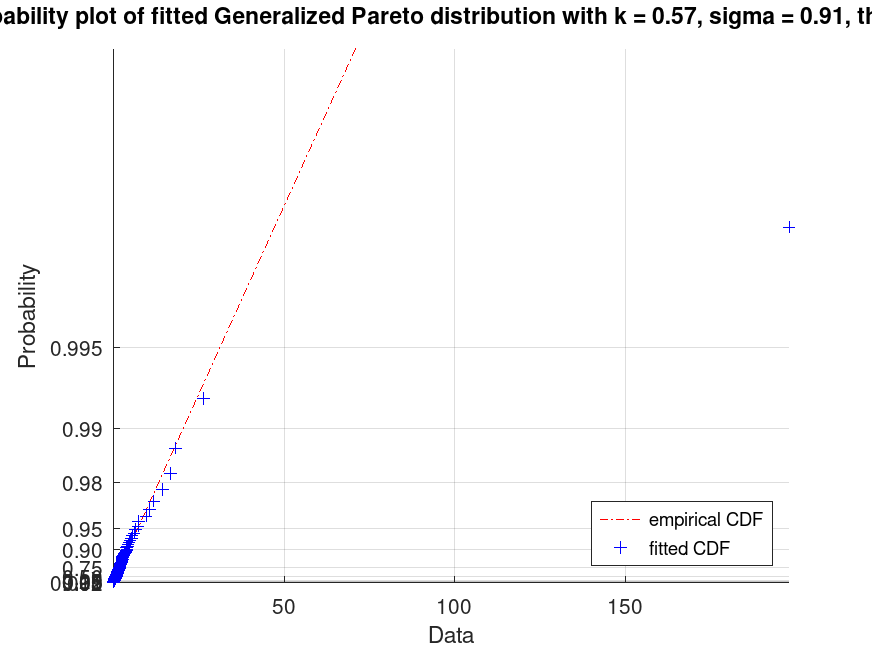
Example: 3


 ## Generate a data set of 200 random samples from a Generalized Pareto
 ## distribution with parameters k = 0.5, sigma = 1, theta = 0. Display a probability
 ## plot for the Generalized Pareto distribution fit to the data (fixing theta=0).

 pd_fixed = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 rand ("seed", 21);
 data = random (pd_fixed, 200, 1);
 pd_fitted = GeneralizedParetoDistribution.fit (data, 0)
 plot (pd_fitted, "PlotType", "probability")
 txt = strcat ("Probability plot of fitted Generalized Pareto", ...
               " distribution with k = %0.2f, sigma = %0.2f, theta = 0");
 title (sprintf (txt, pd_fitted.k, pd_fitted.sigma))
 legend ({"empirical CDF", "fitted CDF"}, "location", "southeast")

 ## This creates a probability plot to compare the fitted distribution to the
 ## data, useful for checking if the Generalized Pareto model is appropriate for tails.

pd_fixed =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

pd_fitted =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.571492   [0.367911, 0.775073]
    sigma = 0.907212   [0.718512, 1.14547]
    theta =        0

GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum)
GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum, "Display", display)
GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum, setparam)
GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum, setparam, "Display", display)

[nlogL, param] = proflik (pd, pnum) returns a vector nlogL of negative loglikelihood values and a vector param of corresponding parameter values for the parameter in the position indicated by pnum. By default, proflik uses the lower and upper bounds of the 95% confidence interval and computes 100 equispaced values for the selected parameter. pd must be fitted to data.

[nlogL, param] = proflik (pd, pnum, "Display", "on") also plots the profile likelihood against the default range of the selected parameter.

[nlogL, param] = proflik (pd, pnum, setparam) defines a user-defined range of the selected parameter.

[nlogL, param] = proflik (pd, pnum, setparam, "Display", "on") also plots the profile likelihood against the user-defined range of the selected parameter.

For the Generalized Pareto distribution, pnum = 1 selects the parameter k, pnum = 2 selects the parameter sigma, and pnum = 3 selects the parameter theta.

When opted to display the profile likelihood plot, proflik also plots the baseline loglikelihood computed at the lower bound of the 95% confidence interval and estimated maximum likelihood. The latter might not be observable if it is outside of the used-defined range of parameter values.

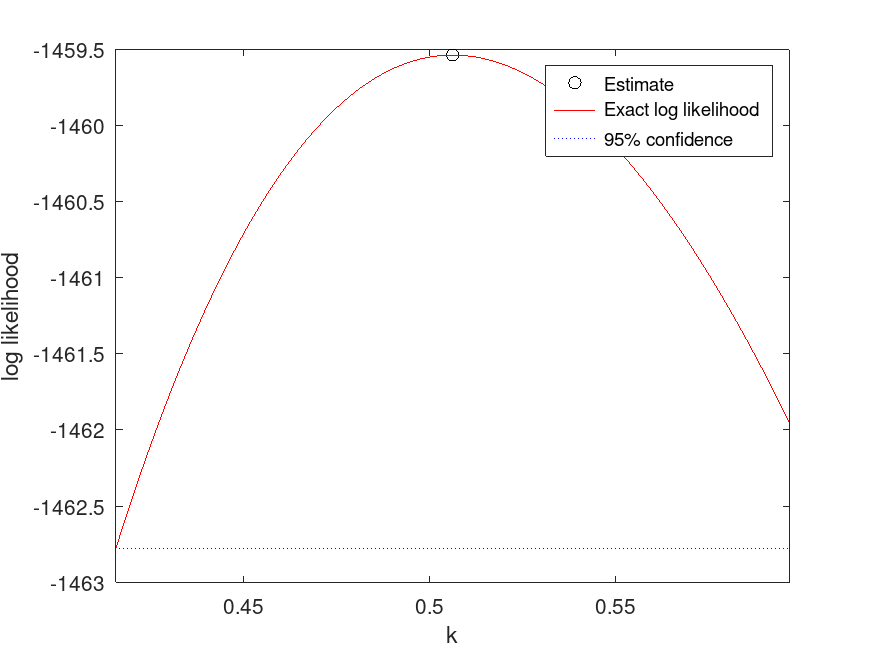
Example: 1


 ## Compute and plot the profile likelihood for the shape parameter of a fitted
 ## Generalized Pareto distribution
 pd = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 rand ("seed", 21);
 data = random (pd, 1000, 1);
 pd_fitted = GeneralizedParetoDistribution.fit (data, 0)
 [nlogL, param] = proflik (pd_fitted, 1, "Display", "on");

 ## Use this to analyze the profile likelihood of the shape parameter (k),
 ## helping to understand the uncertainty in parameter estimates for tail behavior.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

pd_fitted =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.506107   [0.415558, 0.596656]
    sigma =   0.9545   [0.85923, 1.06033]
    theta =        0

GeneralizedParetoDistribution: r = random (pd)
GeneralizedParetoDistribution: r = random (pd, rows)
GeneralizedParetoDistribution: r = random (pd, rows, cols, …)
GeneralizedParetoDistribution: r = random (pd, [sz])

r = random (pd) returns a random number from the distribution object pd.

When called with a single size argument, random returns a square matrix with the dimension specified. When called with more than one scalar argument, the first two arguments are taken as the number of rows and columns and any further arguments specify additional matrix dimensions. The size may also be specified with a row vector of dimensions, sz.

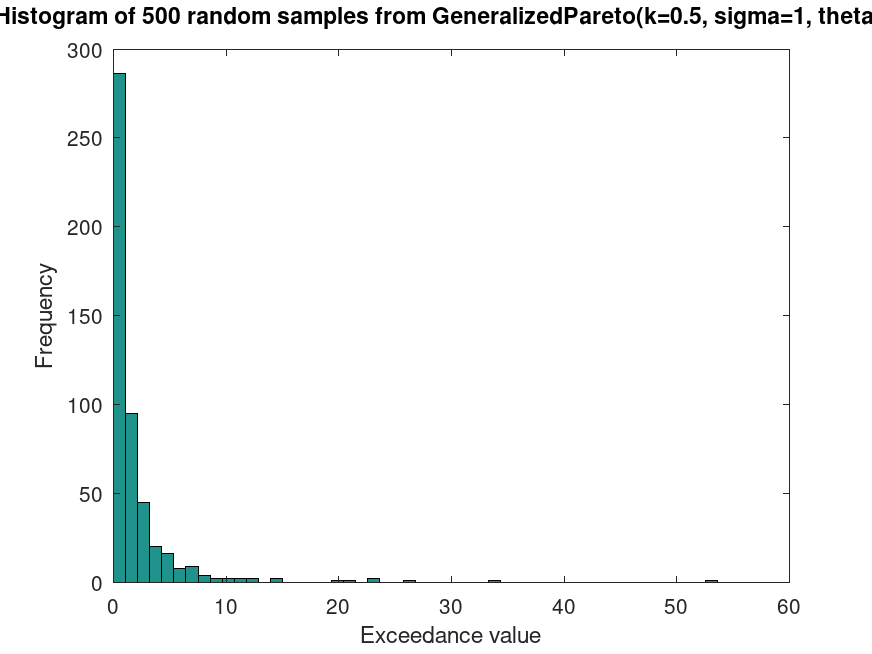
Example: 1


 ## Generate random samples from a Generalized Pareto distribution
 pd = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 rand ("seed", 25);
 samples = random (pd, 500, 1);
 hist (samples, 50)
 title ("Histogram of 500 random samples from GeneralizedPareto(k=0.5, sigma=1, theta=0)")
 xlabel ("Exceedance value")
 ylabel ("Frequency")

 ## This generates random samples from a Generalized Pareto distribution, useful
 ## for simulating extreme exceedances in risk modeling.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

GeneralizedParetoDistribution: s = std (pd)

s = std (pd) computes the standard deviation of the probability distribution object, pd.

Example: 1


 ## Compute the standard deviation for a Generalized Pareto distribution
 pd = makedist ("GeneralizedPareto", "k", 0.3, "sigma", 1, "theta", 0)
 std_value = std (pd)

 ## Use this to calculate the standard deviation, which measures the variability
 ## in exceedance values (finite only if k<0.5).

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.3
    sigma =   1
    theta =   0

std_value = 2.2588

GeneralizedParetoDistribution: t = truncate (pd, lower, upper)

t = truncate (pd, lower, upper) returns a probability distribution t, which is the probability distribution pd truncated to the specified interval with lower limit, lower, and upper limit, upper. If pd is fitted to data with fitdist, the returned probability distribution t is not fitted, does not contain any data or estimated values, and it is as it has been created with the makedist function, but it includes the truncation interval.

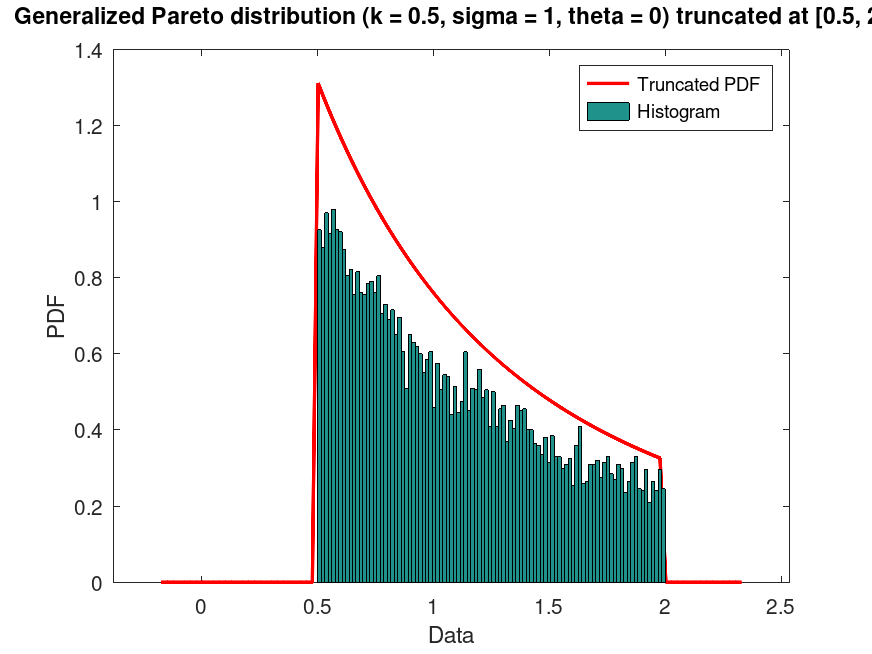
Example: 1


 ## Plot the PDF of a Generalized Pareto distribution, with parameters k = 0.5, sigma = 1, theta = 0,
 ## truncated at [0.5, 2] intervals. Generate 10000 random samples from this truncated distribution
 ## and superimpose a histogram scaled accordingly

 pd = makedist ("GeneralizedPareto", "k", 0.5, "sigma", 1, "theta", 0)
 t = truncate (pd, 0.5, 2)
 rand ("seed", 21);
 data = random (t, 10000, 1);

 ## Plot histogram and fitted PDF
 plot (t)
 hold on
 hist (data, 100, 50)
 hold off
 title ("Generalized Pareto distribution (k = 0.5, sigma = 1, theta = 0) truncated at [0.5, 2]")
 legend ("Truncated PDF", "Histogram")

 ## This demonstrates truncating a Generalized Pareto distribution to a specific
 ## range and visualizing the resulting distribution with random samples.

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0

t =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.5
    sigma =   1
    theta =   0
  Truncated to the interval [0.5, 2]

GeneralizedParetoDistribution: v = var (pd)

v = var (pd) computes the variance of the probability distribution object, pd.

Example: 1


 ## Compute the variance for a Generalized Pareto distribution
 pd = makedist ("GeneralizedPareto", "k", 0.3, "sigma", 1, "theta", 0)
 var_value = var (pd)

 ## Use this to calculate the variance, which quantifies the spread of the
 ## exceedance values in the distribution (finite only if k<0.5).

pd =
  GeneralizedParetoDistribution

  Generalized Pareto distribution
        k = 0.3
    sigma =   1
    theta =   0

var_value = 5.1020

Categories &

Functions List

Clustering

Clustering

Classification Classes

Classification Classes

Clustering Classes

Clustering Classes

Regression Classes

Regression Classes

Data Manipulation

Data Manipulation

Descriptive Statistics

Descriptive Statistics

Distribution Classes

Distribution Classes

Distribution Fitting

Distribution Fitting

Distribution Functions

Distribution Functions

Distribution Statistics

Distribution Statistics

Distribution Wrappers

Distribution Wrappers

Experimental Design

Experimental Design

Machine Learning

Machine Learning

Model Fitting

Model Fitting

Hypothesis Testing

Hypothesis Testing

I/O

I/O

Plotting

Plotting

Regression

Regression

Transforms

Transforms

Class Definition: GeneralizedParetoDistribution

statistics: GeneralizedParetoDistribution

Properties

k

Example: 1

Example: 2

sigma

Example: 1

Example: 2

theta

Example: 1

Example: 2

DistributionName

NumParameters

ParameterNames

ParameterDescription

ParameterValues

ParameterCovariance

ParameterIsFixed

Truncation

IsTruncated

InputData

Methods

cdf

GeneralizedParetoDistribution: p = cdf (pd, x)

GeneralizedParetoDistribution: p = cdf (pd, x, "upper")

Example: 1

icdf

GeneralizedParetoDistribution: x = icdf (pd, p)

Example: 1

iqr

GeneralizedParetoDistribution: r = iqr (pd)

Example: 1

mean

GeneralizedParetoDistribution: m = mean (pd)

Example: 1

median

GeneralizedParetoDistribution: m = median (pd)

Example: 1

negloglik

Class Definition: `GeneralizedParetoDistribution`

`k`

`sigma`

`theta`

`DistributionName`

`NumParameters`

`ParameterNames`

`ParameterDescription`

`ParameterValues`

`ParameterCovariance`

`ParameterIsFixed`

`Truncation`

`IsTruncated`

`InputData`

`cdf`

`GeneralizedParetoDistribution: p = cdf (pd, x)`

`GeneralizedParetoDistribution: p = cdf (pd, x, "upper")`

`icdf`

`GeneralizedParetoDistribution: x = icdf (pd, p)`

`iqr`

`GeneralizedParetoDistribution: r = iqr (pd)`

`mean`

`GeneralizedParetoDistribution: m = mean (pd)`

`median`

`GeneralizedParetoDistribution: m = median (pd)`

`negloglik`

`GeneralizedParetoDistribution: nlogL = negloglik (pd)`

`paramci`

`GeneralizedParetoDistribution: ci = paramci (pd)`

`GeneralizedParetoDistribution: ci = paramci (pd, Name, Value)`

`pdf`

`GeneralizedParetoDistribution: y = pdf (pd, x)`

`plot`

`GeneralizedParetoDistribution: plot (pd)`

`GeneralizedParetoDistribution: plot (pd, Name, Value)`

`GeneralizedParetoDistribution: h = plot (…)`

`proflik`

`GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum)`

`GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum, "Display", display)`

`GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum, setparam)`

`GeneralizedParetoDistribution: [nlogL, param] = proflik (pd, pnum, setparam, "Display", display)`

`random`

`GeneralizedParetoDistribution: r = random (pd)`

`GeneralizedParetoDistribution: r = random (pd, rows)`

`GeneralizedParetoDistribution: r = random (pd, rows, cols, …)`

`GeneralizedParetoDistribution: r = random (pd, [sz])`

`std`

`GeneralizedParetoDistribution: s = std (pd)`

`truncate`

`GeneralizedParetoDistribution: t = truncate (pd, lower, upper)`

`var`

`GeneralizedParetoDistribution: v = var (pd)`