Categories &

Functions List

Function Reference: bisacdf

statistics: p = bisacdf (x, beta, gamma)
statistics: p = bisacdf (x, beta, gamma, "upper")

Birnbaum-Saunders cumulative distribution function (CDF).

For each element of x, compute the cumulative distribution function (CDF) of the Birnbaum-Saunders distribution with scale parameter beta and shape parameter gamma. The size of p is the common size of x, beta and gamma. A scalar input functions as a constant matrix of the same size as the other inputs.

p = bisacdf (x, beta, gamma, "upper") computes the upper tail probability of the Birnbaum-Saunders distribution with parameters beta and gamma, at the values in x.

Further information about the Birnbaum-Saunders distribution can be found at https://en.wikipedia.org/wiki/Birnbaum%E2%80%93Saunders_distribution

See also: bisainv, bisapdf, bisarnd, bisafit, bisalike, bisastat

Source Code: bisacdf

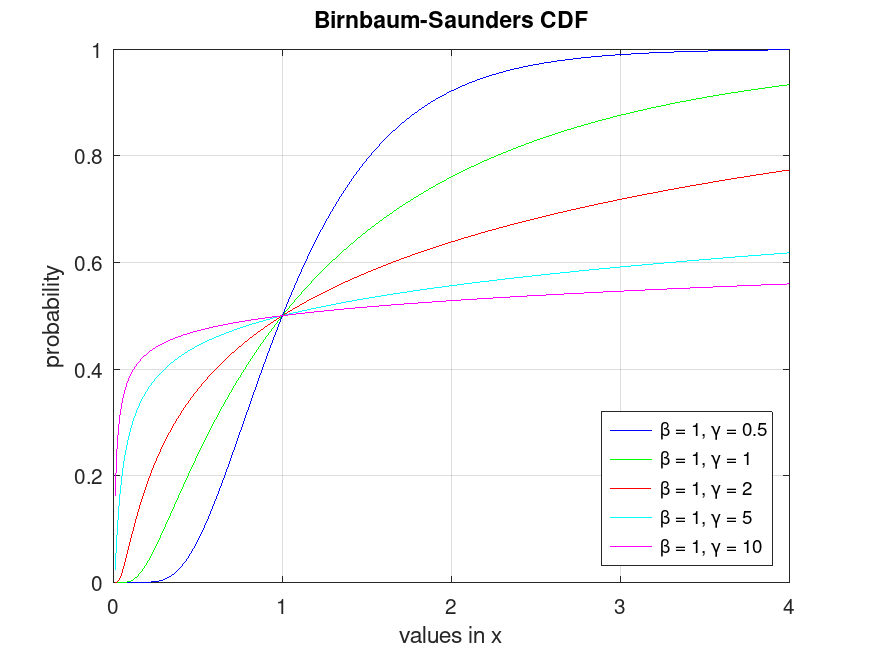
Example: 1

  

 ## Plot various CDFs from the Birnbaum-Saunders distribution
 x = 0.01:0.01:4;
 p1 = bisacdf (x, 1, 0.5);
 p2 = bisacdf (x, 1, 1);
 p3 = bisacdf (x, 1, 2);
 p4 = bisacdf (x, 1, 5);
 p5 = bisacdf (x, 1, 10);
 plot (x, p1, "-b", x, p2, "-g", x, p3, "-r", x, p4, "-c", x, p5, "-m")
 grid on
 legend ({"β = 1, γ = 0.5", "β = 1, γ = 1", "β = 1, γ = 2", ...
          "β = 1, γ = 5", "β = 1, γ = 10"}, "location", "southeast")
 title ("Birnbaum-Saunders CDF")
 xlabel ("values in x")
 ylabel ("probability")
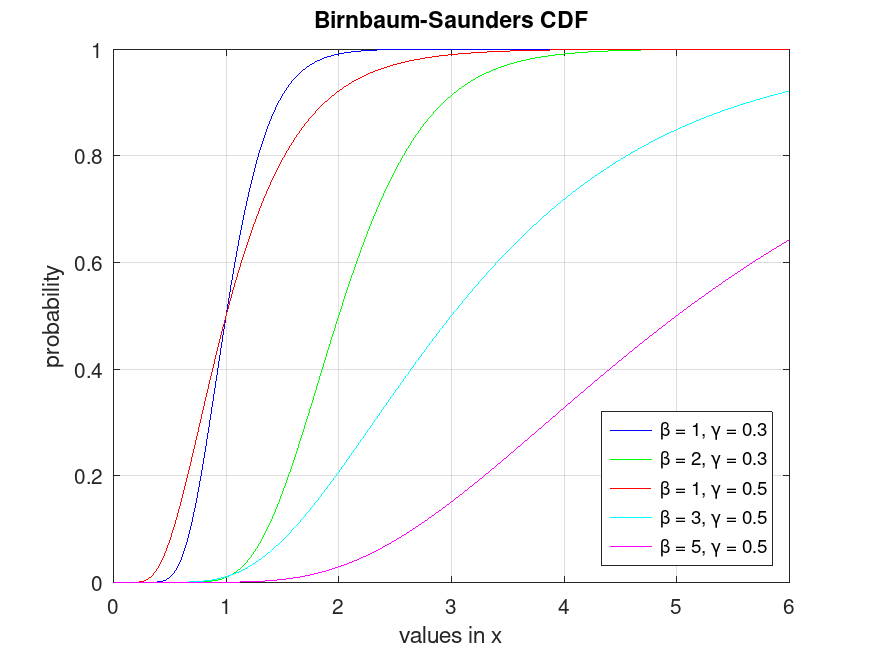
plotted figure

Example: 2

  

 ## Plot various CDFs from the Birnbaum-Saunders distribution
 x = 0.01:0.01:6;
 p1 = bisacdf (x, 1, 0.3);
 p2 = bisacdf (x, 2, 0.3);
 p3 = bisacdf (x, 1, 0.5);
 p4 = bisacdf (x, 3, 0.5);
 p5 = bisacdf (x, 5, 0.5);
 plot (x, p1, "-b", x, p2, "-g", x, p3, "-r", x, p4, "-c", x, p5, "-m")
 grid on
 legend ({"β = 1, γ = 0.3", "β = 2, γ = 0.3", "β = 1, γ = 0.5", ...
          "β = 3, γ = 0.5", "β = 5, γ = 0.5"}, "location", "southeast")
 title ("Birnbaum-Saunders CDF")
 xlabel ("values in x")
 ylabel ("probability")
plotted figure