Categories &

Functions List

Function Reference: gpfit

statistics: paramhat = gpfit (x, theta)
statistics: [paramhat, paramci] = gpfit (x, theta)
statistics: [paramhat, paramci] = gpfit (x, theta, alpha)
statistics: [paramhat, paramci] = gpfit (x, theta, alpha, options)

Estimate parameters and confidence intervals for the generalized Pareto distribution.

paramhat = gpfit (x, theta) returns the maximum likelihood estimates of the parameters of the generalized Pareto distribution given the data in x and the location parameter theta. paramhat(1) is the shape parameter, k, paramhat(2) is the scale parameter, sigma, and paramhat(3) is the location parameter, theta. Although theta is returned in the estimated paramhat, gpfit does not estimate the location parameter theta, and it must be assumed to be known, given as a fixed parameter in input argument theta.

[paramhat, paramci] = gpfit (x, theta) returns the 95% confidence intervals for the estimated parameter k and sigma. The third colummn of paramci includes the location parameter theta without any confidence bounds.

[…] = gpfit (x, theta, alpha) also returns the 100 * (1 - alpha) percent confidence intervals for the parameter estimates. By default, the optional argument alpha is 0.05 corresponding to 95% confidence intervals. Pass in [] for alpha to use the default values.

[…] = gpfit (x, theta, alpha, options) specifies control parameters for the iterative algorithm used to compute ML estimates with the fminsearch function. options is a structure with the following fields and their default values:

  • options.Display = "off"
  • options.MaxFunEvals = 400
  • options.MaxIter = 200
  • options.TolX = 1e-6

When k = 0 and theta = 0, the Generalized Pareto is equivalent to the exponential distribution. When k > 0 and theta = k / k the Generalized Pareto is equivalent to the Pareto distribution. The mean of the Generalized Pareto is not finite when k >= 1 and the variance is not finite when k >= 1/2. When k >= 0, the Generalized Pareto has positive density for x > theta, or, when theta < 0, for 0 <= (x - theta) / sigma <= -1 / k.

Further information about the generalized Pareto distribution can be found at https://en.wikipedia.org/wiki/Generalized_Pareto_distribution

See also: gpcdf, gpinv, gppdf, gprnd, gplike, gpstat

Source Code: gpfit

Example: 1

  

 ## Sample 2 populations from different generalized Pareto distibutions
 ## Assume location parameter θ is known
 theta = 0;
 rand ("seed", 5);    # for reproducibility
 r1 = gprnd (1, 2, theta, 20000, 1);
 rand ("seed", 2);    # for reproducibility
 r2 = gprnd (3, 1, theta, 20000, 1);
 r = [r1, r2];

 ## Plot them normalized and fix their colors
 hist (r, [0.1:0.2:100], 5);
 h = findobj (gca, "Type", "patch");
 set (h(1), "facecolor", "r");
 set (h(2), "facecolor", "c");
 ylim ([0, 1]);
 xlim ([0, 5]);
 hold on

 ## Estimate their α and β parameters
 k_sigmaA = gpfit (r(:,1), theta);
 k_sigmaB = gpfit (r(:,2), theta);

 ## Plot their estimated PDFs
 x = [0.01, 0.1:0.2:18];
 y = gppdf (x, k_sigmaA(1), k_sigmaA(2), theta);
 plot (x, y, "-pc");
 y = gppdf (x, k_sigmaB(1), k_sigmaB(2), theta);
 plot (x, y, "-sr");
 hold off
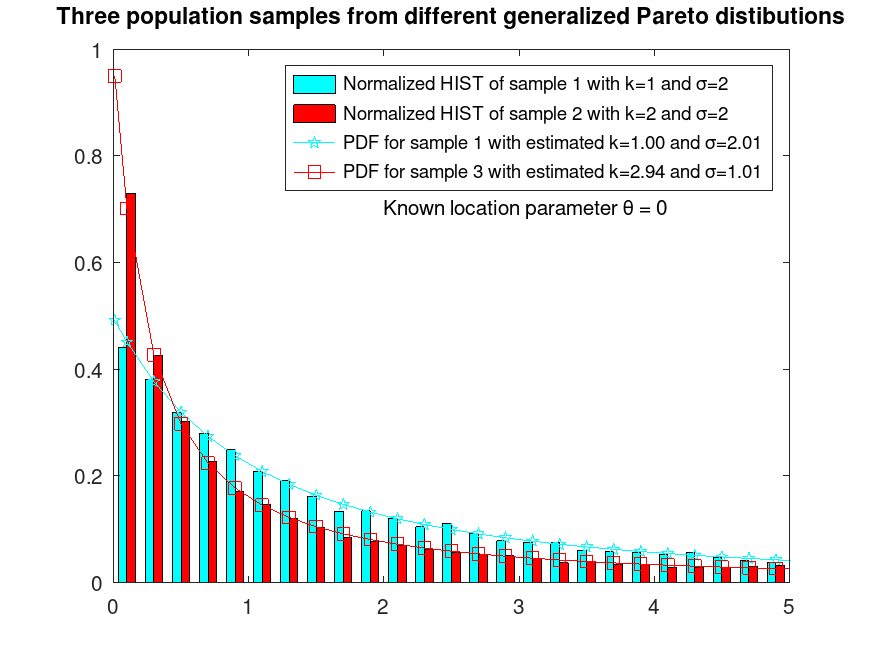
 legend ({"Normalized HIST of sample 1 with k=1 and σ=2", ...
          "Normalized HIST of sample 2 with k=2 and σ=2", ...
          sprintf("PDF for sample 1 with estimated k=%0.2f and σ=%0.2f", ...
                  k_sigmaA(1), k_sigmaA(2)), ...
          sprintf("PDF for sample 3 with estimated k=%0.2f and σ=%0.2f", ...
                  k_sigmaB(1), k_sigmaB(2))})
 title ("Three population samples from different generalized Pareto distibutions")
 text (2, 0.7, "Known location parameter θ = 0")
 hold off
plotted figure