Categories &

Functions List

Function Reference: gpinv

statistics: x = gpinv (p, k, sigma, theta)

Inverse of the generalized Pareto cumulative distribution function (iCDF).

For each element of p, compute the quantile (the inverse of the CDF) of the generalized Pareto distribution with shape parameter k, scale parameter sigma, and location parameter theta. The size of x is the common size of p, k, sigma, and theta. A scalar input functions as a constant matrix of the same size as the other inputs.

When k = 0 and theta = 0, the Generalized Pareto is equivalent to the exponential distribution. When k > 0 and theta = k / k the Generalized Pareto is equivalent to the Pareto distribution. The mean of the Generalized Pareto is not finite when k >= 1 and the variance is not finite when k >= 1/2. When k >= 0, the Generalized Pareto has positive density for x > theta, or, when theta < 0, for 0 <= (x - theta) / sigma <= -1 / k.

Further information about the generalized Pareto distribution can be found at https://en.wikipedia.org/wiki/Generalized_Pareto_distribution

See also: gpcdf, gppdf, gprnd, gpfit, gplike, gpstat

Source Code: gpinv

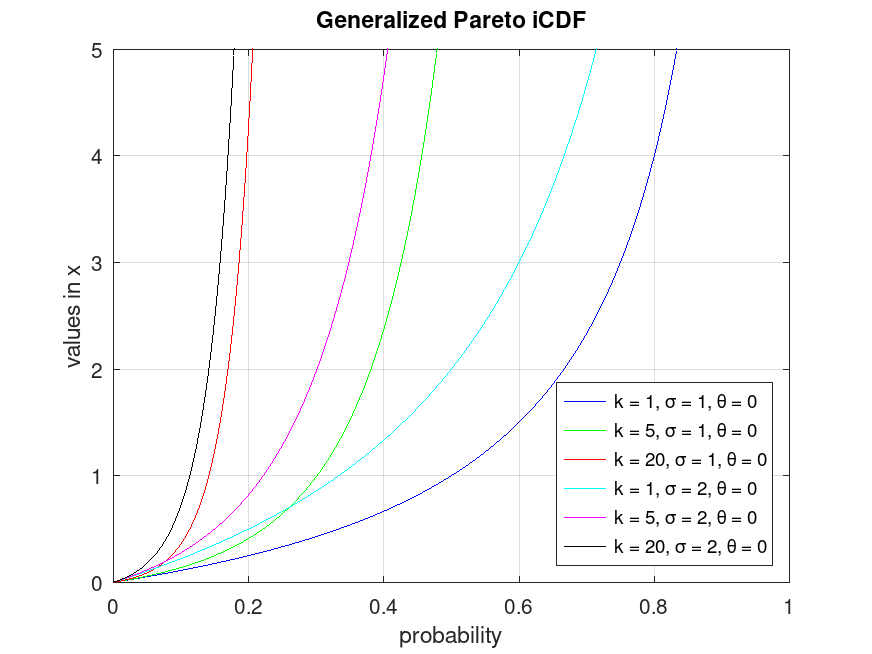
Example: 1

  

 ## Plot various iCDFs from the generalized Pareto distribution
 p = 0.001:0.001:0.999;
 x1 = gpinv (p, 1, 1, 0);
 x2 = gpinv (p, 5, 1, 0);
 x3 = gpinv (p, 20, 1, 0);
 x4 = gpinv (p, 1, 2, 0);
 x5 = gpinv (p, 5, 2, 0);
 x6 = gpinv (p, 20, 2, 0);
 plot (p, x1, "-b", p, x2, "-g", p, x3, "-r", ...
       p, x4, "-c", p, x5, "-m", p, x6, "-k")
 grid on
 ylim ([0, 5])
 legend ({"k = 1, σ = 1, θ = 0", "k = 5, σ = 1, θ = 0", ...
          "k = 20, σ = 1, θ = 0", "k = 1, σ = 2, θ = 0", ...
          "k = 5, σ = 2, θ = 0", "k = 20, σ = 2, θ = 0"}, ...
         "location", "southeast")
 title ("Generalized Pareto iCDF")
 xlabel ("probability")
 ylabel ("values in x")
plotted figure