Categories &

Functions List

Function Reference: glmfit

statistics: b = glmfit (X, y, distribution)
statistics: b = glmfit (X, y, distribution, Name, Value)
statistics: [b, dev] = glmfit (…)
statistics: [b, dev, stats] = glmfit (…)

Perform generalized linear model fitting.

b = glmfit (X, y, distribution) returns a vector b of coefficient estimates for a generalized linear regression model of the responses in y on the predictors in X, using the distribution defined in distribution.

  • X is an n×p numeric matrix of predictor variables with n observations and p predictors.
  • y is an n×1 numeric vector of responses for all supported distributions, except for the ’binomial’ distribution in which case y can be either a numeric or logical n×1 vector or an n×2 matrix, where the first column contains the number of successes and the second column contains the number of trials.
  • distribution is a character vector specifying the distribution of the response variable. Supported distributions are "normal", "binomial", "poisson", "gamma", and "inverse gaussian".

b = glmfit (…, Name, Value) specifies additional options using Name-Value pair arguments.

NameValue
"B0"A numeric vector specifying initial values for the coefficient estimates. By default, the initial values are fitted values fitted from the data.
"Constant"A character vector specifying whether to include a constant term in the model. Valid options are "on" (default) and "off".
"EstDisp"A character vector specifying whether to compute dispersion parameter. Valid options are "on" and "off". For "binomial" and "poisson" distributions the default is "off", whereas for the "normal", "gamma", and "inverse gaussian" distributions the default is "on".
"link"A character vector specifying the name of a canonical link function or a numeric scalar for specifying a "power" link function. Supported canonical link functions include "identity" (default for "normal" distribution), "log" (default for "poisson" distribution), "logit" (default for "binomial" distribution), "probit", "loglog", "comploglog", and "reciprocal" (default for the "gamma" distribution). The "power" link function is the default for the "inverse gaussian" distribution with p = -2. For custom link functions, the user can provide cell array with three function handles: the link function, its derivative, and its inverse, or alternatively a structure S with three fields: S.Link, S.Derivative, and S.Inverse. Each field can either contain a function handle or a character vector with the name of an existing function. All custom link functions must accept a vector of inputs and return a vector of the same size.
"Offset"A numeric vector of the same length as the response y specifying an offset variable in the fit. It is used as an additional predictor with a coefficient value fixed at 1.
"Options"A scalar structure containing the fields MaxIter and TolX. MaxIter must be a scalar positive integer specifying the maximum number of iteration allowed for fitting the model, and TolX must be a positive scalar value specifying the termination tolerance.
"Weights"An n×1 numeric vector of nonnegative values, where n is the number of observations in X. By default, it is ones (n, 1).

[b, dev] = glmfit (…) also returns the deviance of the fit as a numeric value in dev. Deviance is a generalization of the residual sum of squares. It measures the goodness of fit compared to a saturated model.

[b, dev, stats] = glmfit (…) also returns the structure stats, which contains the model statistics in the following fields:

  • beta - Coefficient estimates b
  • dfe - Degrees of freedom for error
  • sfit - Estimated dispersion parameter
  • s - Theoretical or estimated dispersion parameter
  • estdisp - false when "EstDisp" is "off" and true when "EstDisp" is "on"
  • covb - Estimated covariance matrix for b
  • se - Vector of standard errors of the coefficient estimates b
  • coeffcorr - Correlation matrix for b
  • t - t statistics for b
  • p - p-values for b
  • resid - Vector of residuals
  • residp - Vector of Pearson residuals
  • residd - Vector of deviance residuals
  • resida - Vector of Anscombe residuals

See also: glmval

Source Code: glmfit

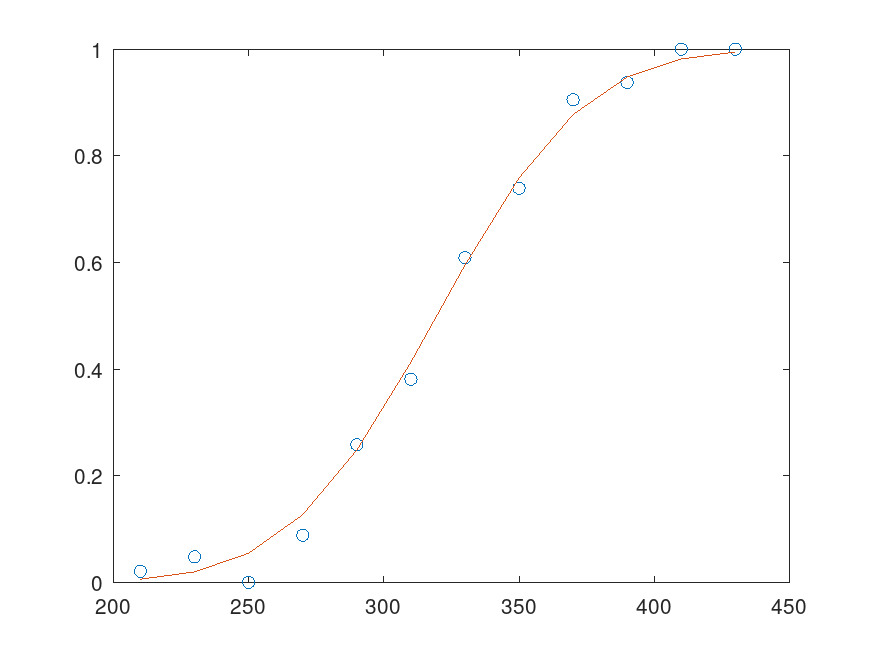
Example: 1

  

 x = [210, 230, 250, 270, 290, 310, 330, 350, 370, 390, 410, 430]';
 n = [48, 42, 31, 34, 31, 21, 23, 23, 21, 16, 17, 21]';
 y = [1, 2, 0, 3, 8, 8, 14, 17, 19, 15, 17, 21]';
 b = glmfit (x, [y n], "binomial", "Link", "probit");
 yfit = glmval (b, x, "probit", "Size", n);
 plot (x, y./n, 'o', x, yfit ./ n, '-')
plotted figure

Example: 2

  

 load fisheriris
 X = meas (51:end, :);
 y = strcmp ("versicolor", species(51:end));
 b = glmfit (X, y, "binomial", "link", "logit")

b =

   42.6378
    2.4652
    6.6809
   -9.4294
  -18.2861