Categories &

Functions List

Function Reference: rangesearch

statistics: idx = rangesearch (X, Y, r)
statistics: [idx, D] = rangesearch (X, Y, r)
statistics: […] = rangesearch (…, name, value)

Find all neighbors within specified distance from input data.

idx = rangesearch (X, Y, r) returns all the points in X that are within distance r from the points in Y. X must be an N×P numeric matrix of input data, where rows correspond to observations and columns correspond to features or variables. Y is an M×P numeric matrix with query points, which must have the same numbers of column as X. r must be a nonnegative scalar value. idx is an M×1 cell array, where M is the number of observations in Y. The vector Idx{j} contains the indices of observations (rows) in X whose distances to Y(j,:) are not greater than r.

[idx, D] = rangesearch (X, Y, r) also returns the distances, D, which correspond to the points in X that are within distance r from the points in Y. D is an M×1 cell array, where M is the number of observations in Y. The vector D{j} contains the indices of observations (rows) in X whose distances to Y(j,:) are not greater than r.

Additional parameters can be specified by Name-Value pair arguments.

NameValue
"P"is the Minkowski distance exponent and it must be a positive scalar. This argument is only valid when the selected distance metric is "minkowski". By default it is 2.
"Scale"is the scale parameter for the standardized Euclidean distance and it must be a nonnegative numeric vector of equal length to the number of columns in X. This argument is only valid when the selected distance metric is "seuclidean", in which case each coordinate of X is scaled by the corresponding element of "scale", as is each query point in Y. By default, the scale parameter is the standard deviation of each coordinate in X.
"Cov"is the covariance matrix for computing the mahalanobis distance and it must be a positive definite matrix matching the the number of columns in X. This argument is only valid when the selected distance metric is "mahalanobis".
"BucketSize"is the maximum number of data points in the leaf node of the Kd-tree and it must be a positive integer. This argument is only valid when the selected search method is "kdtree".
"SortIndices"is a boolean flag to sort the returned indices in ascending order by distance and it is true by default. When the selected search method is "exhaustive" or the "IncludeTies" flag is true, rangesearch always sorts the returned indices.
"Distance"is the distance metric used by rangesearch as specified below:
"euclidean"Euclidean distance.
"seuclidean"standardized Euclidean distance. Each coordinate difference between the rows in X and the query matrix Y is scaled by dividing by the corresponding element of the standard deviation computed from X. To specify a different scaling, use the "Scale" name-value argument.
"cityblock"City block distance.
"chebychev"Chebychev distance (maximum coordinate difference).
"minkowski"Minkowski distance. The default exponent is 2. To specify a different exponent, use the "P" name-value argument.
"mahalanobis"Mahalanobis distance, computed using a positive definite covariance matrix. To change the value of the covariance matrix, use the "Cov" name-value argument.
"cosine"Cosine distance.
"correlation"One minus the sample linear correlation between observations (treated as sequences of values).
"spearman"One minus the sample Spearman’s rank correlation between observations (treated as sequences of values).
"hamming"Hamming distance, which is the percentage of coordinates that differ.
"jaccard"One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ.
@distfunCustom distance function handle. A distance function of the form function D2 = distfun (XI, YI), where XI is a 1×P vector containing a single observation in P-dimensional space, YI is an N×P matrix containing an arbitrary number of observations in the same P-dimensional space, and D2 is an N×P vector of distances, where (D2k) is the distance between observations XI and (YIk,:).
"NSMethod"is the nearest neighbor search method used by rangesearch as specified below.
"kdtree"Creates and uses a Kd-tree to find nearest neighbors. "kdtree" is the default value when the number of columns in X is less than or equal to 10, X is not sparse, and the distance metric is "euclidean", "cityblock", "manhattan", "chebychev", or "minkowski". Otherwise, the default value is "exhaustive". This argument is only valid when the distance metric is one of the four aforementioned metrics.
"exhaustive"Uses the exhaustive search algorithm by computing the distance values from all the points in X to each point in Y.

See also: knnsearch, pdist2

Source Code: rangesearch

Example: 1

  

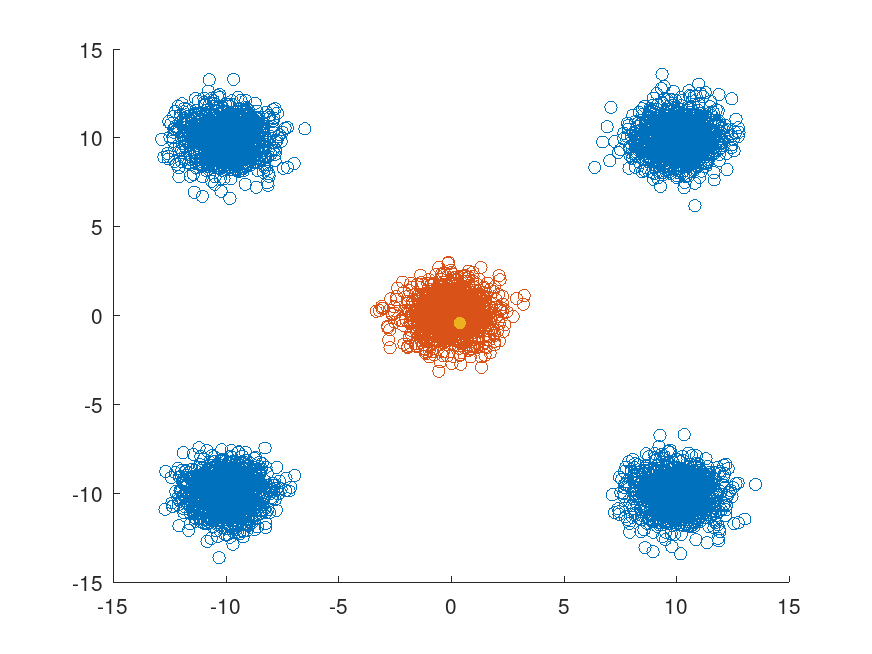
 ## Generate 1000 random 2D points from each of five distinct multivariate
 ## normal distributions that form five separate classes
 N = 1000;
 d = 10;
 randn ("seed", 5);
 X1 = mvnrnd (d * [0, 0], eye (2), 1000);
 randn ("seed", 6);
 X2 = mvnrnd (d * [1, 1], eye (2), 1000);
 randn ("seed", 7);
 X3 = mvnrnd (d * [-1, -1], eye (2), 1000);
 randn ("seed", 8);
 X4 = mvnrnd (d * [1, -1], eye (2), 1000);
 randn ("seed", 8);
 X5 = mvnrnd (d * [-1, 1], eye (2), 1000);
 X = [X1; X2; X3; X4; X5];

 ## For each point in X, find the points in X that are within a radius d
 ## away from the points in X.
 Idx = rangesearch (X, X, d, "NSMethod", "exhaustive");

 ## Select the first point in X (corresponding to the first class) and find
 ## its nearest neighbors within the radius d.  Display these points in
 ## one color and the remaining points in a different color.
 x = X(1,:);
 nearestPoints = X (Idx{1},:);
 nonNearestIdx = true (size (X, 1), 1);
 nonNearestIdx(Idx{1}) = false;

 scatter (X(nonNearestIdx,1), X(nonNearestIdx,2))
 hold on
 scatter (nearestPoints(:,1),nearestPoints(:,2))
 scatter (x(1), x(2), "black", "filled")
 hold off

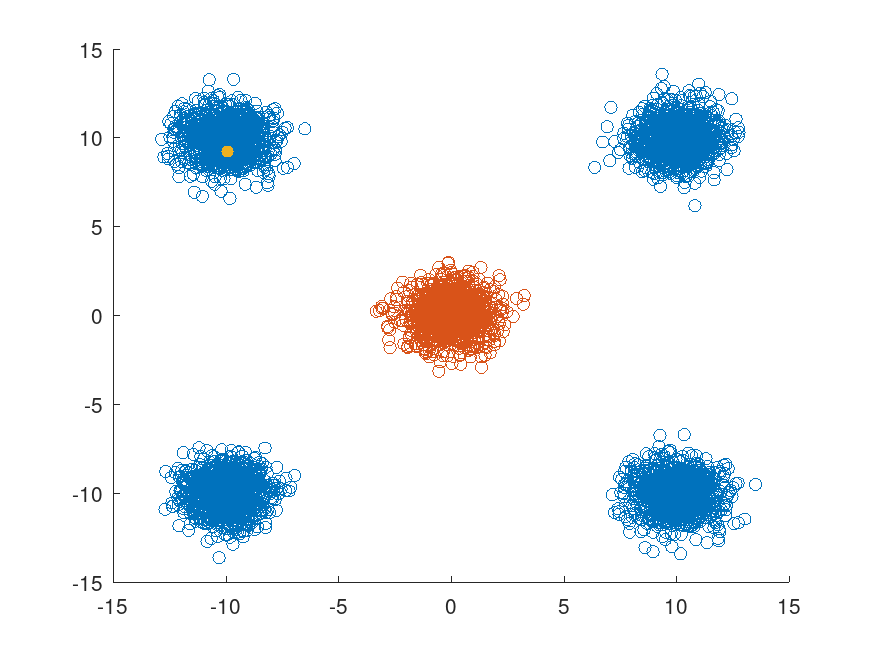
 ## Select the last point in X (corresponding to the fifth class) and find
 ## its nearest neighbors within the radius d.  Display these points in
 ## one color and the remaining points in a different color.
 x = X(end,:);
 nearestPoints = X (Idx{1},:);
 nonNearestIdx = true (size (X, 1), 1);
 nonNearestIdx(Idx{1}) = false;

 figure
 scatter (X(nonNearestIdx,1), X(nonNearestIdx,2))
 hold on
 scatter (nearestPoints(:,1),nearestPoints(:,2))
 scatter (x(1), x(2), "black", "filled")
 hold off
plotted figure

plotted figure