Categories &

Functions List

Class Definition: ExhaustiveSearcher

statistics: ExhaustiveSearcher

Exhaustive nearest neighbor searcher class.

The ExhaustiveSearcher class implements an exhaustive search algorithm for nearest neighbor queries. It stores training data and supports various distance metrics along with their parameter values for performing an exhaustive search. The exhaustive search algorithm computes the distance from each query point to all the points in the training data and facilitates a nearest neighbor search using knnsearch or a radius search using rangesearch.

You can either use the ExhaustiveSearcher class constructor or the createns function to create an ExhaustiveSearcher object.

See also: createns, KDTreeSearcher, hnswSearcher, knnsearch, rangesearch

Source Code: ExhaustiveSearcher

Properties

Point data, specified as an N×P numeric matrix where each row is an observation and each column is a feature. This property is private and cannot be modified after object creation.

Distance metric used for searches, specified as a character vector (e.g., "euclidean", "minkowski") or a function handle to a custom distance function. Default is "euclidean". Supported metrics align with those in pdist2.

The type and value of the distance parameter depends on the selected Distance metric and can be any of the following:

  • For "minkowski", a positive scalar exponent (default 2).
  • For "seuclidean", a nonnegative vector of scaling factors matching the number of columns in X (default is standard deviation of X).
  • For "mahalanobis", a positive definite covariance matrix matching the dimensions of X (default is cov (X)).
  • Empty for other metrics or custom functions.

Methods

ExhaustiveSearcher: obj = ExhaustiveSearcher (X)
ExhaustiveSearcher: obj = ExhaustiveSearcher (X, name, value)

obj = ExhaustiveSearcher (X) constructs an ExhaustiveSearcher object with training data X using the default "euclidean" distance metric. X must be an N×P numeric matrix, where rows represent observations and columns represent features.

obj = ExhaustiveSearcher (X, name, value) allows customization through name-value pairs:

NameValue
"Distance"Distance metric, specified as a character vector (e.g., "euclidean", "minkowski") or a function handle. Default is "euclidean". See pdist2 for supported metrics.
"P"a positive scalar specifying the exponent for the Minkowski distance. Valid only when "Distance" is "minkowski". Default is 2.
"Scale"a nonnegative vector with the same number of elements as the columns in X specifying the scale parameter for the standardized Euclidean distance. Valid only when "Distance" is "seuclidean". Default is std (X).
"Cov"a positive definite matrix matching the number of columns in X specifying the covariance matrix for the Mahalanobis distance. Valid only when "Distance" is "mahalanobis". Default is cov (X).

See also: ExhaustiveSearcher, knnsearch, rangesearch, pdist2

ExhaustiveSearcher: [idx, D] = knnsearch (obj, Y)
ExhaustiveSearcher: [idx, D] = knnsearch (obj, Y, name, value)

[idx, D] = knnsearch (obj, Y) returns the indices idx and distances D of the nearest neighbor in obj.X to each point in Y, using the distance metric specified in obj.Distance.

  • obj is an ExhaustiveSearcher object.
  • Y is an M×P numeric matrix of query points, where P must match the number of columns in obj.X.

[idx, D] = knnsearch (obj, Y, name, value) allows additional options via name-value pairs:

NameValue
"K"A positive integer specifying the number of nearest neighbors to find. Default is 1.
"IncludeTies"Logical flag indicating whether to include all neighbors tied with the Kth smallest distance. Default is false. If true, idx and D are cell arrays.

idx contains the indices of the nearest neighbors in obj.X. D contains the corresponding distances.

See also: ExhaustiveSearcher, rangesearch, pdist2

ExhaustiveSearcher: [idx, D] = rangesearch (obj, Y, r)
ExhaustiveSearcher: [idx, D] = rangesearch (obj, Y, r, name, value)

[idx, D] = rangesearch (obj, Y, r) returns the indices idx and distances D of all points in obj.X within radius r of each point in Y, using the distance metric specified in obj.Distance.

  • obj is an ExhaustiveSearcher object.
  • Y is an M×P numeric matrix of query points, where P must match the number of columns in obj.X.
  • r is a nonnegative scalar specifying the search radius.

[idx, D] = rangesearch (…, name, value) allows additional options via name-value pairs:

NameValue
"SortIndices"Logical flag indicating whether to sort the indices by distance. Default is true.

idx and D are cell arrays where each cell contains the indices and distances for one query point in Y.

See also: ExhaustiveSearcher, knnsearch, pdist2

Examples

  
 load fisheriris
 rng('default');
 numSamples = size (meas, 1);
 queryIndices = [20, 95, 123, 136, 138];
 dataPoints = meas(~ismember (1:numSamples, queryIndices), :);
 queryPoints = meas(queryIndices, :);
 searchModel = ExhaustiveSearcher (dataPoints, 'Distance', 'mahalanobis')
 mahalanobisParam = searchModel.DistParameter
 searchRadius = 3;
 nearestNeighbors = knnsearch (searchModel, queryPoints, "K", 2)
 neighborsInRange = rangesearch (searchModel, queryPoints, searchRadius)
  
searchModel =

  ExhaustiveSearcher with properties:

                 Distance: 'mahalanobis'
            DistParameter: [4x4 double]
                        X: [145x4 double]
mahalanobisParam =

   0.654708  -0.036803   1.231971   0.502620
  -0.036803   0.191363  -0.322715  -0.119293
   1.231971  -0.322715   3.067148   1.284234
   0.502620  -0.119293   1.284234   0.579984

nearestNeighbors =

     5     6
    98    95
   104   128
   135    65
   102   115

neighborsInRange =
  5x1 cell array

Columns 1 through 1:

    {[  5 6 21 46 48 44 37 22 1 8 11 27 26 33 18 12 39 7 40 49 32 47 19 3 28 29 17 20 43 23 42 16 30 4 56 34 ... ]}    
    {[ 98 95 83 88 78 89 55 63 69 91 94 90 82 92 59 80 100 138 131 57 66 67 81 61 125 102 115 145 134 96 110 ... ]}    
    {[  104 128 127 106 117 123 58 52 76 50 107 86 74 101 65 75 77 131 96 72 54 73 115 129 51 63 67 91 71 87 ... ]}    
    {[135 65 75 101 111 117 77 54 50 86 137 52 76 119 141 128 74 71 121 142 143 136 58 124 51 109 110 104 68 ... ]}    
    {[ 102 115 91 94 63 56 145 83 88 95 55 131 66 85 122 78 70 103 125 73 98 84 134 123 51 90 126 67 100 138 ... ]}
  
 X = [1, 2; 3, 4; 5, 6];
 obj = ExhaustiveSearcher (X);
 ## Find the nearest neighbor to [2, 3]
 Y = [2, 3];
 [idx, D] = knnsearch (obj, Y);
 disp ("Nearest neighbor index:"); disp (idx);
 disp ("Distance:"); disp (D);
 ## Find all points within radius 2
 [idx, D] = rangesearch (obj, Y, 2);
 disp ("Indices within radius:"); disp (idx);
 disp ("Distances:"); disp (D);
  
Nearest neighbor index:
1
Distance:
1.4142
Indices within radius:
  1x1 cell array

    {[1 2]}    

Distances:
  1x1 cell array

    {[1.41421 1.41421]}
  
 X = [0, 0; 1, 0; 0, 1];
 obj = ExhaustiveSearcher (X, "Distance", "minkowski", "P", 1);
 ## Find the 2 nearest neighbors to [0.5, 0.5]
 Y = [0.5, 0.5];
 [idx, D] = knnsearch (obj, Y, "K", 2);
 disp ("Nearest neighbor indices:"); disp (idx);
 disp ("Distances:"); disp (D);
  
Nearest neighbor indices:
   1   2
Distances:
   1   1
  
 rng(42);
 disp('Demonstrating ExhaustiveSearcher');

 n = 100;
 mu1 = [0.3, 0.3];
 mu2 = [0.7, 0.7];
 sigma = 0.1;
 X1 = mu1 + sigma * randn(n/2, 2);
 X2 = mu2 + sigma * randn(n/2, 2);
 X = [X1; X2];

 obj = ExhaustiveSearcher(X);

 Y = [0.3, 0.3; 0.7, 0.7; 0.5, 0.5];

 K = 5;
 [idx, D] = knnsearch(obj, Y, "K", K);

 disp('For the first query point:');
 disp(['Query point: ', num2str(Y(1,:))]);
 disp('Indices of nearest neighbors:');
 disp(idx(1,:));
 disp('Distances:');
 disp(D(1,:));

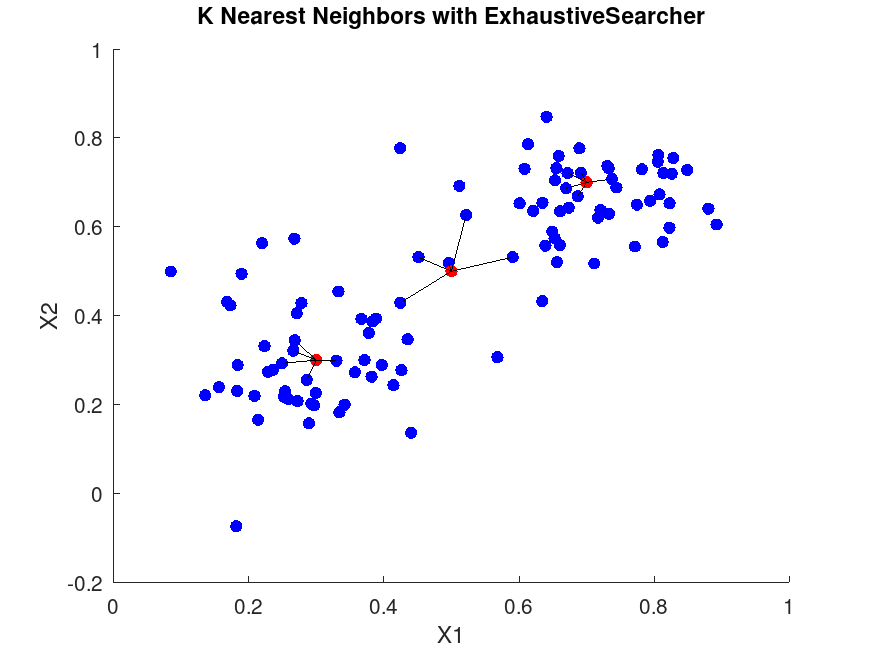
 figure;
 scatter(X(:,1), X(:,2), 36, 'b', 'filled'); % Training points
 hold on;
 scatter(Y(:,1), Y(:,2), 36, 'r', 'filled'); % Query points
 for i = 1:size(Y,1)
     query = Y(i,:);
     neighbors = X(idx(i,:), :);
     for j = 1:K
         plot([query(1), neighbors(j,1)], [query(2), neighbors(j,2)], 'k-');
     end
 end
 hold off;
 title('K Nearest Neighbors with ExhaustiveSearcher');
 xlabel('X1');
 ylabel('X2');

 r = 0.15;
 [idx, D] = rangesearch(obj, Y, r);

 disp('For the first query point in rangesearch:');
 disp(['Query point: ', num2str(Y(1,:))]);
 disp('Indices of points within radius:');
 disp(idx{1});
 disp('Distances:');
 disp(D{1});

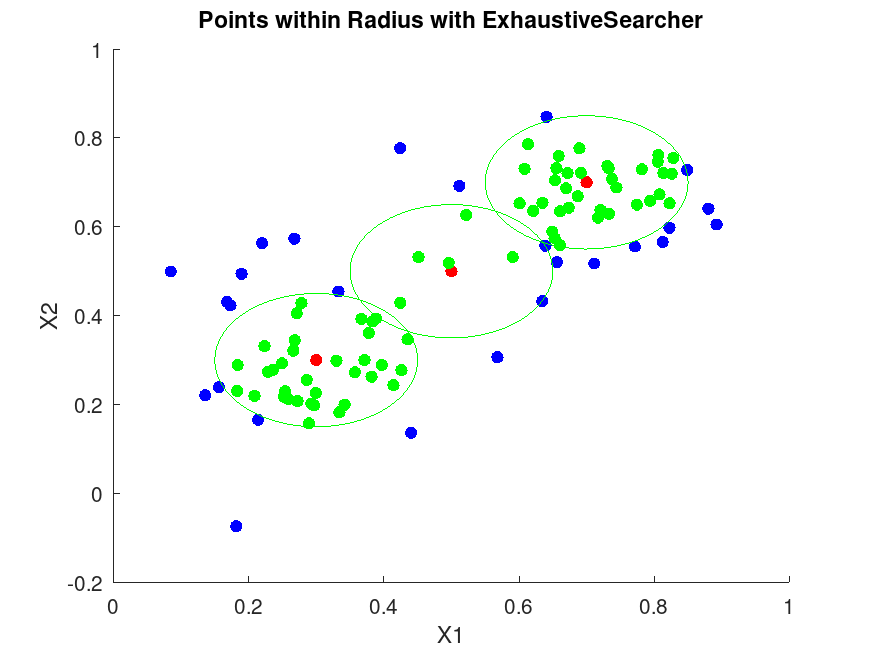
 figure;
 scatter(X(:,1), X(:,2), 36, 'b', 'filled');
 hold on;
 scatter(Y(:,1), Y(:,2), 36, 'r', 'filled');
 theta = linspace(0, 2*pi, 100);
 for i = 1:size(Y,1)
     center = Y(i,:);
     x_circle = center(1) + r * cos(theta);
     y_circle = center(2) + r * sin(theta);
     plot(x_circle, y_circle, 'g-');
     % Highlight points within radius
     if ~isempty(idx{i})
         in_radius = X(idx{i}, :);
         scatter(in_radius(:,1), in_radius(:,2), 36, 'g', 'filled');
     end
 end
 hold off;
 title('Points within Radius with ExhaustiveSearcher');
 xlabel('X1');
 ylabel('X2');
  
Demonstrating ExhaustiveSearcher
For the first query point:
Query point: 0.3         0.3
Indices of nearest neighbors:
   49   19   14   46   34
Distances:
   0.029932   0.040026   0.046845   0.051107   0.054789
For the first query point in rangesearch:
Query point: 0.3         0.3
Indices of points within radius:
 Columns 1 through 23:

   49   19   14   46   34   23   12   41    1    3   42   48   24    2   11   37   10   27   32   20   44   40   39

 Columns 24 through 34:

   21    7   31   45   30    4   16   47    9   29    8
Distances:
 Columns 1 through 10:

   0.029932   0.040026   0.046845   0.051107   0.054789   0.063517   0.067855   0.071365   0.073769   0.075991

 Columns 11 through 20:

   0.082686   0.084066   0.090008   0.095171   0.096337   0.096836   0.097593   0.098255   0.098948   0.101780

 Columns 21 through 30:

   0.108652   0.108983   0.114272   0.116760   0.120198   0.121721   0.122560   0.127342   0.128062   0.128687

 Columns 31 through 34:

   0.130208   0.136007   0.142870   0.143009
plotted figure

plotted figure