Statistics: KDTreeSearcher

Class Definition: `KDTreeSearcher`

statistics: KDTreeSearcher

KD-tree nearest neighbor searcher class.

The KDTreeSearcher class implements a KD-tree search algorithm for nearest neighbor queries. It stores training data and supports various distance metrics along with their parameter values for performing a KD-tree search. The KD-tree algorithm partitions the training data into a hierarchical tree structure and performs search operations by traversing the tree to reduce the number of distance computations. It facilitates a nearest neighborsearch using knnsearch or a radius search using rangesearch.

You can either use the KDTreeSearcher class constructor or the createns function to create an KDTreeSearcher object.

Source Code: KDTreeSearcher

Properties

Point data, specified as an $N×P$ numeric matrix where each row is an observation and each column is a feature. This property is private and cannot be modified after object creation.

The maximum number of data points in the leaf node of the KD-tree. Default value is 50. This property is private and cannot be modified after object creation.

Distance metric used for searches, specified as a character vector. Supported metrics are "euclidean", "cityblock", "minkowski", and "chebychev". Default value is "euclidean".

The type and value of the distance parameter depends on the selected Distance metric and can be any of the following:

For "minkowski", a positive scalar exponent (default 2).
Empty for other metrics ("euclidean", "cityblock", "chebychev"). Attempting to set a non-empty value for these metrics will result in an error.

Methods

KDTreeSearcher: obj = KDTreeSearcher (X)
KDTreeSearcher: obj = KDTreeSearcher (X, name, value)

obj = KDTreeSearcher (X) constructs a KDTreeSearcher object with training data X using the default "euclidean" distance metric. X must be an $N×P$ numeric matrix, where rows represent observations and columns represent features.

obj = KDTreeSearcher (X, name, value) allows customization through name-value pairs:

`Name`		`Value`
`"Distance"`		Distance metric, specified as a character vector (`"euclidean"`, `"cityblock"`, `"minkowski"`, `"chebychev"`). Default is `"euclidean"`.
`"P"`		Minkowski distance exponent, a positive scalar. Valid only when `"Distance"` is `"minkowski"`. Default is 2.
`"BucketSize"`		Maximum number of data points in the leaf node of the KD-tree, a positive integer. Default is 50.

You can also create a KDTreeSearcher object using the createns function.

See also: KDTreeSearcher, knnsearch, rangesearch, createns

KDTreeSearcher: [idx, D] = knnsearch (obj, Y)
KDTreeSearcher: [idx, D] = knnsearch (obj, Y, name, value)

[idx, D] = knnsearch (obj, Y, K) returns the indices idx and distances D of the $K$ nearest neighbors in obj.X to each point in Y, using the distance metric specified in obj.Distance.

obj is a KDTreeSearcher object.
Y is an $M×P$ numeric matrix of query points, where $P$ must match the number of columns in obj.X.
idx contains the indices of the nearest neighbors in obj.X.
D contains the corresponding distances.

[idx, D] = knnsearch (obj, Y, name, value) allows additional options via name-value pairs:

`Name`		`Value`
`"K"`		A positive integer specifying the number of nearest neighbors to find. Default is 1.
`"IncludeTies"`		Logical flag indicating whether to include all neighbors tied with the $K$ th smallest distance. Default is `false`. If `true`, `idx` and `D` are cell arrays.
`"SortIndices"`		Logical flag indicating whether to sort the indices by distance. Default is `true`.

See also: KDTreeSearcher, rangesearch

KDTreeSearcher: [idx, D] = rangesearch (obj, Y, r)
KDTreeSearcher: [idx, D] = rangesearch (obj, Y, r, name, value)

[idx, D] = rangesearch (obj, Y, r) returns the indices idx and distances D of all points in obj.X within radius r of each point in Y, using the distance metric specified in obj.Distance.

obj is a KDTreeSearcher object.
Y is an $M×P$ numeric matrix of query points, where $P$ must match the number of columns in obj.X.
r is a nonnegative scalar specifying the search radius.

[idx, D] = rangesearch (obj, Y, r, name, value) allows additional options via name-value pairs:

`Name`		`Value`
`"SortIndices"`		Logical flag indicating whether to sort the indices by distance. Default is `true`.

idx and D are cell arrays where each cell contains the indices and distances for one query point in Y.

See also: KDTreeSearcher, knnsearch

Examples

 load fisheriris
 numSamples = size (meas, 1);
 queryIndices = [1, 23, 46, 63, 109];
 dataIndices = ~ismember (1:numSamples, queryIndices);
 queryPoints = meas(queryIndices, :);
 dataPoints = meas(dataIndices, :);
 searchRadius = 0.3;
 kdTree = KDTreeSearcher (dataPoints, 'Distance', 'minkowski')
 nearestNeighbors = knnsearch (kdTree, queryPoints, "K", 2)
 neighborsInRange = rangesearch (kdTree, queryPoints, searchRadius)

kdTree =

  KDTreeSearcher with properties:

               BucketSize: 50
                 Distance: 'minkowski'
            DistParameter: 2
                        X: [145x4 double]
nearestNeighbors =

    17     4
     6     2
     1    12
    89    66
   124   100

neighborsInRange =
  5x1 cell array

    {9x1 double}    
    {0x0 double}    
    {7x1 double}    
    {0x0 double}    
    {0x0 double}

 X = [1, 2; 3, 4; 5, 6];
 obj = KDTreeSearcher (X);
 ## Find the nearest neighbor to [2, 3]
 Y = [2, 3];
 [idx, D] = knnsearch (obj, Y, "K", 1);
 disp ("Nearest neighbor index:");
 disp (idx);
 disp ("Distance:");
 disp (D);
 ## Find all points within radius 2
 [idx, D] = rangesearch (obj, Y, 2);
 disp ("Indices within radius:");
 disp (idx);
 disp ("Distances:");
 disp (D);

Nearest neighbor index:
1
Distance:
1.4142
Indices within radius:
  1x1 cell array

    {2x1 double}    

Distances:
  1x1 cell array

    {2x1 double}

 X = [0, 0; 1, 0; 2, 0];
 obj = KDTreeSearcher (X, "Distance", "minkowski", "P", 3);
 ## Find the nearest neighbor to [1, 0]
 Y = [1, 0];
 [idx, D] = knnsearch (obj, Y, "K", 1);
 disp ("Nearest neighbor index:");
 disp (idx);
 disp ("Distance:");
 disp (D);

Nearest neighbor index:
2
Distance:
0

 rng(42);
 disp('Demonstrating KDTreeSearcher');

 n = 100;
 mu1 = [0.3, 0.3];
 mu2 = [0.7, 0.7];
 sigma = 0.1;
 X1 = mu1 + sigma * randn (n / 2, 2);
 X2 = mu2 + sigma * randn (n / 2, 2);
 X = [X1; X2];

 obj = KDTreeSearcher(X);

 Y = [0.3, 0.3; 0.7, 0.7; 0.5, 0.5];

 K = 5;
 [idx, D] = knnsearch (obj, Y, "K", K);

 disp ('For the first query point:');
 disp (['Query point: ', num2str(Y(1,:))]);
 disp ('Indices of nearest neighbors:');
 disp (idx(1,:));
 disp ('Distances:');
 disp (D(1,:));

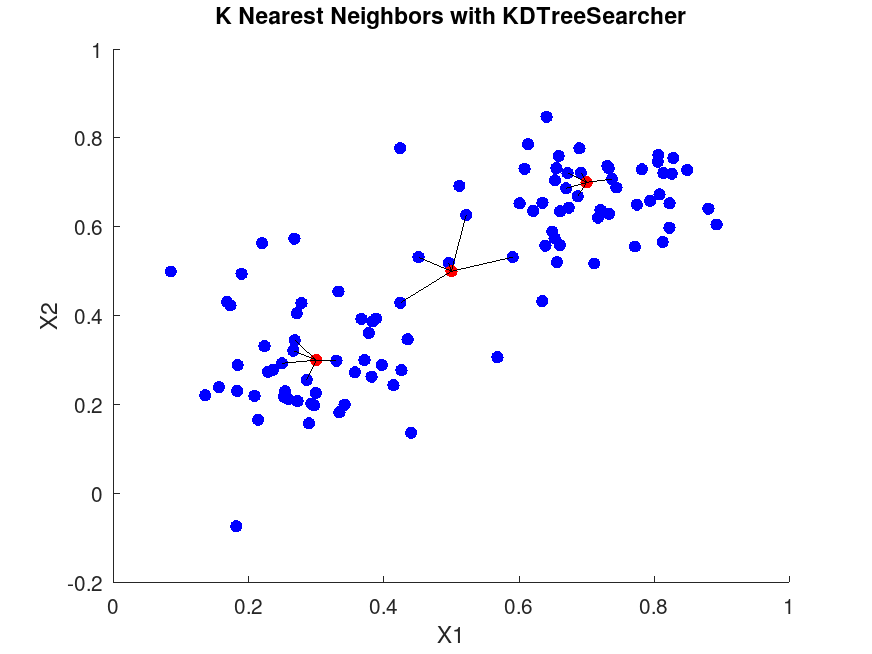
 figure;
 scatter (X(:,1), X(:,2), 36, 'b', 'filled'); # Training points
 hold on;
 scatter (Y(:,1), Y(:,2), 36, 'r', 'filled'); # Query points
 for i = 1:size (Y, 1)
     query = Y(i,:);
     neighbors = X(idx(i,:), :);
     for j = 1:K
         plot ([query(1), neighbors(j,1)], [query(2), neighbors(j,2)], 'k-');
     endfor
 endfor
 hold off;
 title ('K Nearest Neighbors with KDTreeSearcher');
 xlabel ('X1');
 ylabel ('X2');

 r = 0.15;
 [idx, D] = rangesearch (obj, Y, r);

 disp ('For the first query point in rangesearch:');
 disp (['Query point: ', num2str(Y(1,:))]);
 disp ('Indices of points within radius:');
 disp (idx{1});
 disp ('Distances:');
 disp (D{1});

 figure;
 scatter (X(:,1), X(:,2), 36, 'b', 'filled');
 hold on;
 scatter (Y(:,1), Y(:,2), 36, 'r', 'filled');
 theta = linspace (0, 2 * pi, 100);
 for i = 1:size (Y, 1)
     center = Y(i,:);
     x_circle = center(1) + r * cos (theta);
     y_circle = center(2) + r * sin (theta);
     plot (x_circle, y_circle, 'g-');
     ## Highlight points within radius
     if (! isempty (idx{i}))
       in_radius = X(idx{i}, :);
       scatter (in_radius(:,1), in_radius(:,2), 36, 'g', 'filled');
     endif
 endfor
 hold off
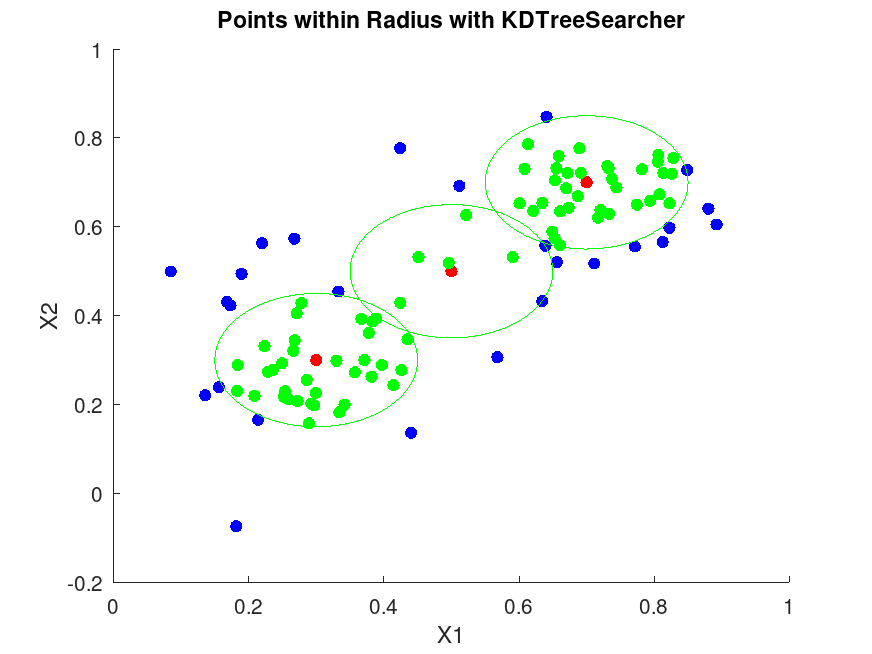
 title ('Points within Radius with KDTreeSearcher');
 xlabel ('X1');
 ylabel ('X2');

Demonstrating KDTreeSearcher
For the first query point:
Query point: 0.3         0.3
Indices of nearest neighbors:
   49   19   14   46   34
Distances:
   0.029932   0.040026   0.046845   0.051107   0.054789
For the first query point in rangesearch:
Query point: 0.3         0.3
Indices of points within radius:
   49
   19
   14
   46
   34
   23
   12
   41
    1
    3
   42
   48
   24
    2
   11
   37
   10
   27
   32
   20
   44
   40
   39
   21
    7
   31
   45
   30
    4
   16
   47
    9
   29
    8
Distances:
   0.029932
   0.040026
   0.046845
   0.051107
   0.054789
   0.063517
   0.067855
   0.071365
   0.073769
   0.075991
   0.082686
   0.084066
   0.090008
   0.095171
   0.096337
   0.096836
   0.097593
   0.098255
   0.098948
   0.101780
   0.108652
   0.108983
   0.114272
   0.116760
   0.120198
   0.121721
   0.122560
   0.127342
   0.128062
   0.128687
   0.130208
   0.136007
   0.142870
   0.143009

Categories &

Functions List

Clustering

Clustering

Classification Classes

Classification Classes

Clustering Classes

Clustering Classes

Regression Classes

Regression Classes

Data Manipulation

Data Manipulation

Descriptive Statistics

Descriptive Statistics

Distribution Classes

Distribution Classes

Distribution Fitting

Distribution Fitting

Distribution Functions

Distribution Functions

Distribution Statistics

Distribution Statistics

Distribution Wrappers

Distribution Wrappers

Experimental Design

Experimental Design

Machine Learning

Machine Learning

Model Fitting

Model Fitting

Hypothesis Testing

Hypothesis Testing

I/O

I/O

Plotting

Plotting

Regression

Regression

Transforms

Transforms

Class Definition: KDTreeSearcher

statistics: KDTreeSearcher

Properties

X

BucketSize

Distance

DistParameter

Methods

KDTreeSearcher

KDTreeSearcher: obj = KDTreeSearcher (X)

KDTreeSearcher: obj = KDTreeSearcher (X, name, value)

knnsearch

KDTreeSearcher: [idx, D] = knnsearch (obj, Y)

KDTreeSearcher: [idx, D] = knnsearch (obj, Y, name, value)

rangesearch

KDTreeSearcher: [idx, D] = rangesearch (obj, Y, r)

KDTreeSearcher: [idx, D] = rangesearch (obj, Y, r, name, value)

Examples

Class Definition: `KDTreeSearcher`

`X`

`BucketSize`

`Distance`

`DistParameter`

`KDTreeSearcher`

`KDTreeSearcher: obj = KDTreeSearcher (X)`

`KDTreeSearcher: obj = KDTreeSearcher (X, name, value)`

`knnsearch`

`KDTreeSearcher: [idx, D] = knnsearch (obj, Y)`

`KDTreeSearcher: [idx, D] = knnsearch (obj, Y, name, value)`

`rangesearch`

`KDTreeSearcher: [idx, D] = rangesearch (obj, Y, r)`

`KDTreeSearcher: [idx, D] = rangesearch (obj, Y, r, name, value)`